一种基于解析规划的多约束再入制导算法*
2013-12-10李强,夏群利,郭涛等
0 引言
亚轨道飞行器是指从地面发射,在完成发射任务后,重新返回地面的跨大气层新型高超声速飞行器。近年来,各国高超声速运载器的发展步伐很快。其中,美国航天运输和X系列试验飞行器的研制[1-2],俄罗斯可重复使用助推器研究[3]等都是发展的焦点。再入制导技术作为飞行器发展的关键技术之一,其任务是使飞行器能够满足各种过程约束及终端约束。目前,再入制导方法主要分为两类:第一类是跟踪预先设计参考剖面的标准轨道制导方法;第二类是利用预测能力对落点参数进行预测的预测制导方法[4]。
再入制导控制变量通常选择为攻角和倾侧角,并将攻角设计为随速度变化的函数,倾侧角作为主要的控制变量调整飞行轨迹。文献[5]基于简化动力学模型,利用平衡滑翔条件,提出了满足各种过程约束和终端约束的解析形式倾侧角指令。文献[6]根据飞行器当前飞行状态和终端条件,迭代计算能够满足终端约束的倾侧角指令,并通过过载、热流等约束对控制指令进行限制修正。文献[7]采用拟平衡滑翔条件将再入走廊约束转化为控制量约束,将参考轨迹的优化设计问题转化为单参数搜索问题,提出基于H-V剖面的轨迹在线生成算法。
文中提出基于H-V剖面的改进再入制导方法,纵向和侧向联合设计,纵向设计H-V参考剖面,侧向设计航向误差走廊,采用反馈线性化方法跟踪H-V剖面确定倾侧角大小,同时根据航向误差走廊确定倾侧角符号,完成控制变量设计。
1 再入轨迹设计的数学模型
亚轨道飞行器再入过程为无动力滑翔,对于无动力再入轨迹设计及制导问题的研究,一般采用三自由度再入动力学模型[8]。
1.1 再入动力学方程
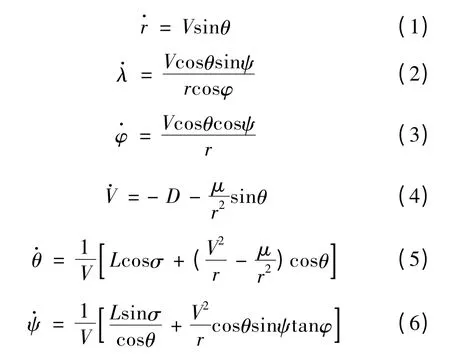
其中,动力学模型中有6个独立状态变量x=(r,λ,φ,V,θ,ψ),分别为高度、经度、纬度、速度、速度倾角和航向角,速度倾角为速度矢量与当地水平面的夹角,向上为正,航向角为速度矢量在当地水平面内的投影与正北方向的夹角,顺时针方向为正;L和D分别为升力和阻力加速度。控制量u=(α,σ),攻角α为事先设计好的攻角-速度函数,因此倾侧角σ是唯一的控制量。
1.2 再入过程约束和终端约束
再入过程通常考虑3个状态过程约束和一个轨迹过程约束,将其描述为再入走廊,状态约束包括最大驻点热流、最大动压和最大过载约束:

同时考虑到减小亚轨道飞行器再入返回时高度震荡,增加平衡滑翔约束[9]:
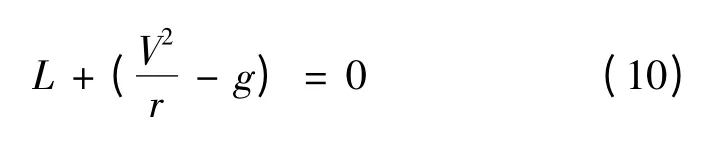
再入终端约束是指飞行器满足末端能量管理段(TAEM)的初始条件,能够实现平稳着陆,其约束条件为:
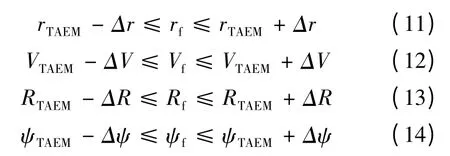
其中,rf、Vf、Rf、ψf分别为飞行器再入终端高度、速度、剩余飞行距离和航向角,rTAEM、VTAEM、RTAEM、ψTAEM分别为末端能量管理段初始高度、速度、剩余飞行距离和航向角,Δr、ΔV、ΔR、Δψ 分别为末端能量管理段初始高度、速度、剩余飞行距离和航向角允许的最大误差。
2 制导方案设计
2.1 基于H-V剖面的纵向参考轨迹规划
纵向参考剖面设计包括初始下降段和过渡段,初始下降段采用常值倾侧角飞行,保证飞行器能够进入再入走廊,并完成平缓过渡;过渡段则根据过渡点参数和末端能量管理约束,在再入走廊内选择优化的四次多项式,完成参考剖面描述,初始段和过渡段联合设计,保证满足终端约束。在再入过程中可以大致认为r=r0+H,且=,其中,r0为地球半径,H为飞行器距地面高度,纵向轨迹设计的规划流程图如图1所示。
2.1.1 初始下降段轨迹规划
初始下降段的设计需要重点考虑驻点热流约束[10]。该段采用常值倾侧角飞行,倾侧角过小可能导致再入轨迹出现跳跃,倾侧角过大则可能超过驻点热流约束,因此初始段应该选择适当的倾侧角,保证飞行器进入再入走廊。判断初始下降段结束的条件是H-V剖面内轨迹指向TAEM初始点,即:

图1 参考剖面规划流程图

其中,δ为一小常数,dH/dV为H-V剖面内当前时刻斜率,由式(16)计算得到:
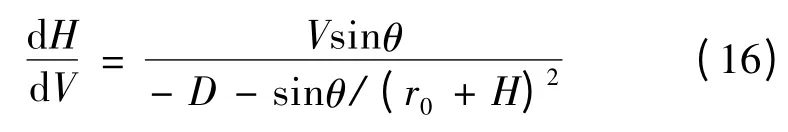
轨迹满足上式后则转入过渡段,该点称为过渡点。
2.1.2 过渡段轨迹规划
过渡段剖面采用四次多项式来描述从过渡点到末端能量管理界面的参考轨迹,即:

其中,ki(i=0,1,2,3,4)为多项式系数。需要5组条件来求解,由于已知过渡点处(VT,HT)、(VT,(dH/dV)T)及 TAEM 界面条件(VTAEM,HTAEM),因此只需再确定两组参数。
考虑多项式在满足初始及终端约束的同时,还需对飞行路径进行约束,可取过渡点与终端点速度中间点M,即:

根据图3再入走廊分析可知,随着速度的降低,速度中点M处的主导约束为动压,HM的选取应保证其轨迹在再入走廊内[10],因此选取该点动压满足式(19),即:
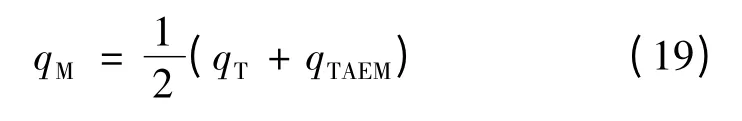
已知M点的速度及动压,则可得到该点高度HM。
将式(17)在TAEM点处求一阶和二阶导数可得:

并将式(18)代入式(17)整理可得:
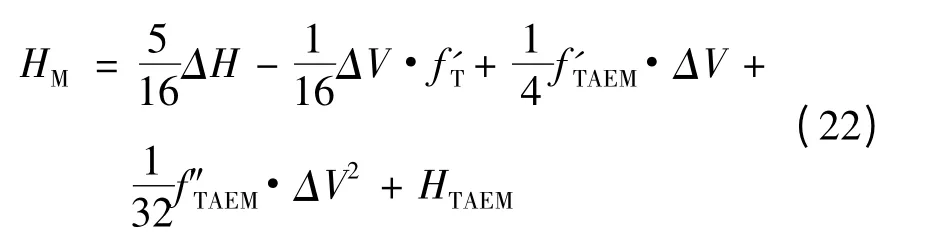
其中ΔH=HT-HTAEM,ΔV=VT-VTAEM,f'T=(dH/dV)T。
对式(16)微分可得:

其中,DV= ∂D/∂V,并且由式= - DVsinθ/hs- 2D2/V及V·=-D-gsinθ得到,hs为标准大气高度参数。
分析可知如果已知TAEM初始点的弹道倾角θTAEM和 σTAEM,即可解得(dH/dV)TAEM和(d2H/dV2)TAEM。并且为了满足终端约束条件,σTAEM可取零。因此将式(16)和式(23)代入式(22)即可求得θTAEM,从而求得f'TAEM和f″TAEM,并进一步确定四次多项式系数,完成H-V参考剖面规划。
定义Rtogo为飞行器到TAEM初始点的航程,并定义当前位置和目标点视线方向与速度矢量的夹角为Δψ,如图2所示。

图2 飞行器与目标点相对关系
当前纵向平面内,剩余航程变化率为:

将纵向平面的航程变化率投影到目标平面,可得到目标平面内的剩余航程变化率:

由于在控制横向航程时,Δψ一般被限制在小角度范围内,近似cosΔψ =1,则:
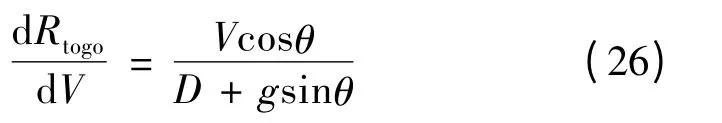
如果过渡段参考剖面确定,式(26)右端项均可得到,则沿着参考剖面积分可得到过渡段剩余航程,结合初始段航程,即可确定在该剖面下到TAEM初始点的总航程,即:
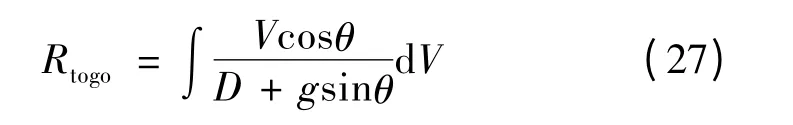
若该航程大于名义航程,则增大初始段的倾侧角指令σ0,使过渡点高度HT下降,从而使整个参考剖面降低,通过增大阻力减小航程,相反则减小初始段倾侧角指令σ0。通过不断迭代计算,最终可得到满足过程约束及终端高度、速度及航程约束的初始倾侧角σ0和参考高度 -速度剖面。图3给出了通过上述算法规划得到的H-V参考剖面。
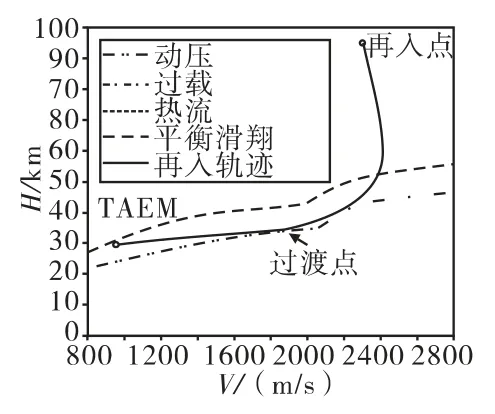
图3 名义参考剖面
2.2 侧向制导设计
通过纵向制导可以确定倾侧角的大小,侧向制导则采用航向误差走廊确定倾侧角的符号。定义航向角误差Δψ为当前速度矢量与飞行器到目标点视线方向的夹角,即Δψ =ψ -ψLOS,其中:

则确定倾侧角反转逻辑为:

其中,ψthreshold为航向误差门限值,通常设计为速度的分段线性函数,其选取原则为既要使再入轨迹满足终端横向位置和角度约束,又要保证滚转反向不要过于频繁,易于工程实现。
3 基于反馈线性化的参考轨迹跟踪算法
飞行器再入动力学为非线性模型,其状态量实时变化,对其参考轨迹跟踪是一个非线性跟踪控制问题。文中采用反馈线性化技术获得自适应非线性跟踪控制算法,完成参考剖面跟踪,与传统的非线性控制方法相比,该方法不再依赖系统运动的求解或稳定性分析,而只需确定系统的反馈形式,使得非线性系统的控制问题变得相对简单。
根据再入动力学方程并忽略地球旋转项影响,同时考虑纵向H-V剖面特性,选取控制输入为u=cosσ,输出为y=H,得到动力学模型为:

定义跟踪误差为当前飞行高度与参考飞行高度之差,即ΔH=H-Hr。并且为了使控制系统具备良好的性能指标,所期望跟踪误差是一个二阶震荡系统,即:

其中:ξ一般取为0.7,ω根据飞行器实际飞行能力确定。
对跟踪误差进行二次微分并结合式(31)可得:

根据式(30)和式(32)得到模型控制输入为:
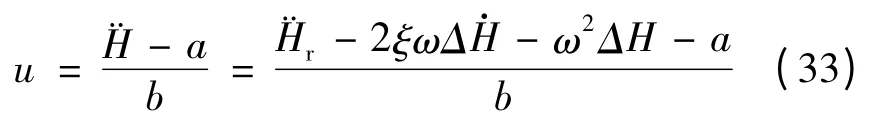
可以看出,控制输入u是包含H、V、θ三个状态变量的非线性输入,通过反馈线性化处理将此非线性系统转化成为二次积分环节。因此得到了基于反馈线性化方法的制导原理框图,如图4所示。

图4 制导系统框图
4 仿真分析
参考航天飞机的攻角方案特点,选择初始攻角为38°;随着速度降低,攻角切换为15°,对应飞行器的最大升阻比条件;末端为了满足TAEM初始点要求,攻角比15°略小,则确定再入飞
行器的名义攻角方案如图5所示。
选取飞行器名义再入初始条件为(H0,λ0,φ0,V0,θ0,ψ0)=(95km,0,0,2300m/s,0,0), 终 端 条 件(HTAEM,VTAEM)=(30km,950m/s),过程约束(Q·s,max,qmax,ny,max)=(250kW/m2,20kPa,4g)。并针对初始条件偏差和环境不确定性,考虑再入过程存在初始高度、初始速度以及大气密度偏差影响,在名义条件上附加偏差状态,进行多种偏差状态的仿真验证,确定多种状态仿真条件如表1所示,并给出了偏差条件下的仿真结果。
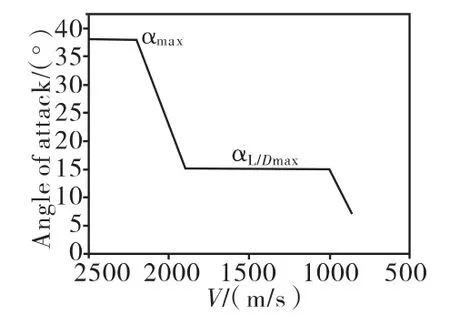
图5 名义攻角曲线
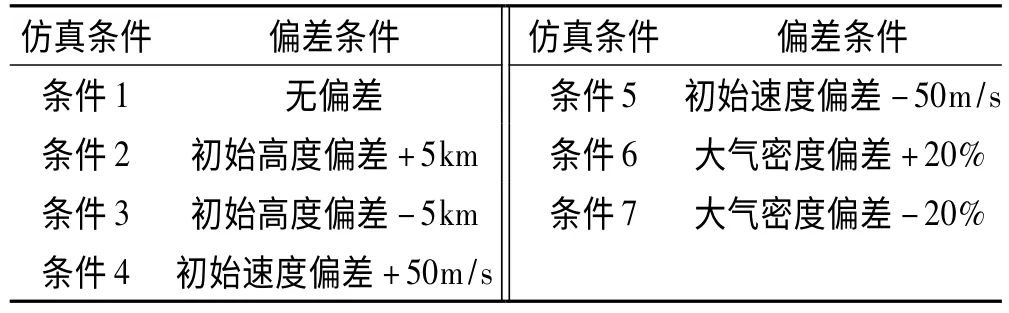
表1 仿真偏差参数表
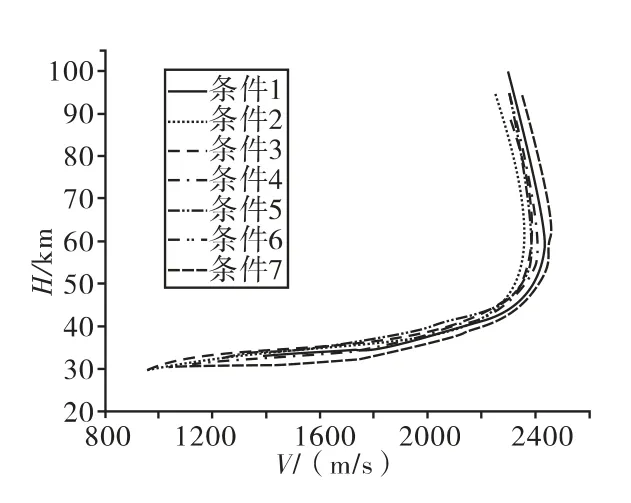
图6 高度-速度剖面
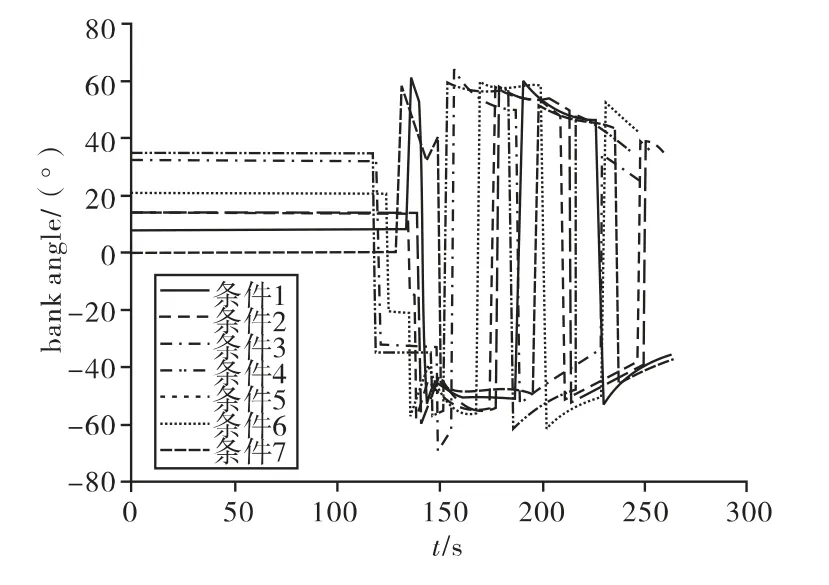
图7 倾侧角变化曲线
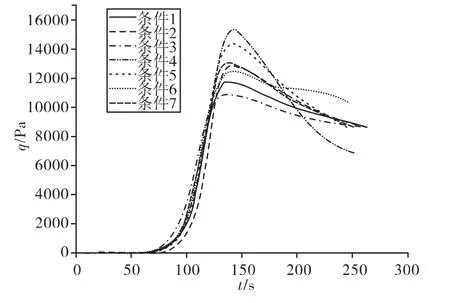
图8 动压变化曲线

图9 过载变化曲线
从图6~图9可以看出,文中提出的再入制导算法在存在初始条件偏差和环境不确定性条件下能够满足终端条件和过程约束,高精度的完成再入段飞行,具备较强鲁棒性。
5 结论
文中提出了基于解析规划的多约束再入制导算法,通过纵、侧向的联合设计,生成满足热流、动压、过载等过程约束和终端高度、速度、航程、航向等终端约束的参考剖面,并利用反馈线性化完成轨迹跟踪。仿真结果表明,该方法能够适应大范围飞行空域和速度的变化,具备一定工程应用价值。
[1]李焱,才满瑞,佟艳春.临近空间飞行器的种类及军事应用[J].中国航天,2007(10):39-44.
[2]Edward B.Near space as a combat space effects enabler[R].USAF,catalyst for air& space power research dialogue,2004.
[3]赵颖.2003年世界运载器发展综述[J].导弹与航天运载技术,2004(2):16-24.
[4]胡建学,陈克俊,赵汉元,等.RLV再入标准轨道制导与轨道预测制导方法比较分析[J].国防科技大学学报,2007,29(1):26 -29.
[5]Horneman K R,Schierman J D.Rapid terminal-trajectory planner for an unpowered launch vehicle[C]//AIAA,Guidance, Navigation and Control Conference, 2009:1-13.
[6]李惠峰,谢陵.基于预测校正方法的RLV再入制导率设计[J].北京航空航天大学学报,2009,35(11):1344-1348.
[7]Shen Z,Lu P.On-board generation of three-dimensional constrained entry trajectories[J].Journal of Guidance,Control and Dynamics,2003,26(1):110 -121.
[8]Nguyen X Vinh,Adolf Busemann,Robert D Culp.Hypersonic and planetary entry flight mechanics[M].University of Michigan Press,1980.
[9]Lu P.Predictor-corrector entry guidance for low lifting vehicles,AIAA,2007-6425[R].2007.
[10]Xue S,Lu P.Constrained predictor-corrector entry guidance[J].Journal of Guidance,Control,and Dynamics,2010,33(4):1273-1281.
