三轴地磁传感器的误差校准算法*

马迎辉，辛长范，徐玉威，陈 铭，雷文星

(中北大学机电工程学院，太原 030051)

0 引言

随着地磁理论的不断完善以及传感器、微处理器和解算算法的日趋成熟，利用磁探测技术测量弹丸的空间姿态已经成为当前测姿和导航研究领域的一个热点。然而采用地磁测量弹丸的空间姿态会产生一定的误差，文中正是基于此种问题设计出了一种新型旋转卡尔曼滤波器来对误差参数进行求解。

以前对于地面姿态测量系统中的三轴地磁传感器采用的校准算法主要是两种，一种是与姿态无关的校准算法，另一种是与姿态相关的校准算法，文中主要描述的是将以前的方法组合从而产生一种新的三轴磁传感器误差校准算法。

1 简介

文中研究的这种新型的误差校准算法特别适合旋转稳定的火箭弹。对于带有更精确传感器的三轴稳定的火箭弹(如陀螺仪)，也可应用其他校准算法。但是这并不妨碍这种算法的实用性。因为通常来讲测量弹体姿态的传感器分为两种，一种是相对粗糙的测量方法(如地磁的姿态测量)，另一种是比较精确的测量方法(如太阳方位传感器)。而文中介绍的这种方法价值在于，在精确校准之前对原始测量数据进行粗校准。

三轴磁传感器校准算法的目的是用来逐步改进估计的参数，通过把每时每刻由地磁测得的数据，从传感器的测量坐标系转换到弹体坐标系，然后对数据进行迭代计算。对常用的传感器模型，这些参数主要包括传感器的偏置，每个轴的比例因子，以及非正交误差。一般常用的粗校准模型只可估计出传感器的偏置。而文中介绍的三轴磁传感器校准算法，当有足够的数据之后就可确定出偏置、比例系数和三轴倾斜角的非正交部分。同时当有来自其他传感器的数据之后，相对于其他传感器的对准误差也可确定出来。

2 逐步校准算法

文中采用的新型三轴磁传感器校准算法是:将与姿态无关和与姿态相关的校准算法组合起来实现磁传感器的误差校准，主要包括以下步骤:

1)首先用一个与姿态无关的三轴磁传感器校准算法来估计出偏置、比例系数和非正交误差。用这些参数对三轴磁传感器的数据实现粗处理。

2)其次用经过校准后的磁传感器和至少一个其他传感器数据来求解姿态历程，如果有多个传感器，指定其中一个作为主要的传感器。

3)最后使用由上一步得到的姿态历程，用一个姿态相关的方法估计出三轴磁传感器的对准误差。利用此对准误差重新对数据进行处理。重复上述两个步骤直到校准误差没有显著的改变为止。

2.1 与姿态无关的三轴磁传感器校准方法

三轴磁传感器的数据本身可以进行自校准，这是基于参考磁场信号幅值的一致性(也就是观测到的地磁信号的幅值是不变的，所以可以根据这些测量数据对其本身进行自校准)，而不需要姿态角、姿态角速度和其他传感器的信息。除了用于迭代校准之外，这个方法本身也是很有用的，特别是在弾箭飞行的初始阶段内，由于在初始阶段内，其他传感器尚未工作或对准误差还没确定出来，因此在这段时间内三轴磁传感器本身的自校准是非常有效的。

并不是所有的三轴磁传感器参数都可以用这种姿态无关的方法解算出来。因为影响测量幅值的参数是可观测的;而影响测量方向的参数是不可观测的。从地面系到测量系的转换可以用矩阵转换来表示。这种九元素的矩阵是正交矩阵和对称矩阵。正交矩阵表示传感器的测量轴相对于弹体轴的刚体转动。对称矩阵的对角线部分表示比例因子，而非对角线则表示为3个轴的倾斜角部分。当只有测量幅值数据可用时，由于矢量的内积随坐标系是不变的，因此传感器的正交对准误差将是不可观测的，但是对于其偏置，比例因子误差却可以估计出来。

2.2 姿态估计算法

对三轴磁传感器的偏置、比例系数进行校正之后，运用三轴磁传感器及其他传感器数据就可确定姿态历程。当前对弹丸的姿态估计有三种方法，第一种是最小二乘的差分校正法，第二种是扩展卡尔曼滤波法，这种方法对具有有效陀螺数据的三轴稳定的火箭弹是非常有用的。最后一种是一个旋转的卡尔曼滤波器，它专门用于旋转稳定的火箭弹。

三轴稳定飞行器的姿态估计器已被广泛应用。而文中介绍的这个旋转卡尔曼滤波器则是一种新型的滤波算法。以前对三轴磁传感器的校准算法都是假设旋转方向是不变的(即在一批数据里他的旋转方向是不变的)，且不考虑力矩和章动力的影响。而文中阐述的这种新型旋转卡尔曼滤波算法则相对更灵活一些，可以应用于姿态和角速度传感器输入数据不断变化的情况。同时也会考虑到环境和控制力矩的影响。

这种旋转的卡尔曼估计器是一种采用了新型的状态矢量的滤波算法，这个状态矢量主要基于三部分:一个是在弹体系下的角动量矢量，另一个是惯性系下的角动量矢量，最后一个是旋转角度。假定外力矩基本不变，这个角动量是慢速变化的，因此所有的快速变化量就被隔离了，这种优势在滤波状态进程中是非常重要的，因为在整个计算过程中这种算法将使数值误差变得很小。

2.3 与姿态相关的三轴磁传感器校准

由以上步骤可获得近似的姿态历程，通过使残差最小可以得到三轴磁传感器对准误差。当然姿态也存在误差，这种误差主要是由不完全校准引起的，但是这种姿态误差将随着每一步的迭代计算而不断减小。

这种与姿态相关的方法用来求解给定姿态的对准误差。它是一个非常高效，可靠的四元数估计算法，可用来求解矢量匹配问题以便使损失函数L最小化。L是一个关于姿态矩阵A的函数:

同样地，对姿态相关的对准估计问题，可以归结为一个相似的形式，也就是:对一个给定的传感器通过使损失函数最小来求解其对准误差

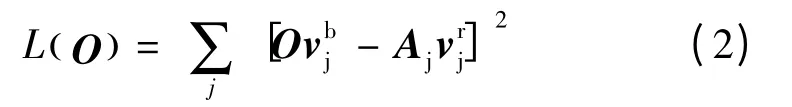
其中，L(O)为正交对准误差O的函数;Aj为已知的姿态历程为给定传感器观测单位矢量。

一旦O确定下来，新的对准误差在传感器坐标系中通常表示为:

其中:N0为校准矩阵;M0为上一次的对准误差。

本方法可能面临的一个复杂性是三轴磁传感器对准误差中的某一个分量OTAM不太好确定。这本身就表明了旋转火箭弹关于旋转轴的对准误差不如其他轴更容易观测。这个问题可以通过求解不相关的另一个传感器的对准误差来得出。这个不相关的传感器通常相对于旋转轴具有较高灵敏度，如太阳方位传感器等。通过把对准误差项组合到一个单一有效的三轴磁传感器对准误差中，然后两个传感器通过 Osensor－2的逆矩阵进行旋转变换:

这样，三轴磁传感器的对准误差就是相对于第二个传感器的对准误差。这样就可以将对准误差计算出来并应用于每次迭代的数据当中。

这种用来确定不相关传感器对准误差的方法根据第二个传感器的类型而不同。如果在弹体坐标系下测量的数据观测范围很宽时，就用姿态估计法。但是当观测范围很小或者在一个旋转周期内测量值变化较大时会使识别误差变得很大。在这种情况下，就选用一个直接的方法来求解关于旋转轴的对准误差。把三轴磁传感器和不相关传感器的观测值以及他们的参考矢量都投影到垂直于旋转轴的一个单位平面上，来找到从参考矢量到观测矢量的平均转角。这些平均的转角就是关于旋转轴的对准误差角。

这样通过每一次迭代，就可计算出一个新的姿态历程，同时也可以计算出一个新的组合校准误差。当组合校准的改变量小于给定的误差范围时，迭代即可停止。

3 仿真算例

假设三轴磁传感器关于3个旋转轴的误差如表1所示。

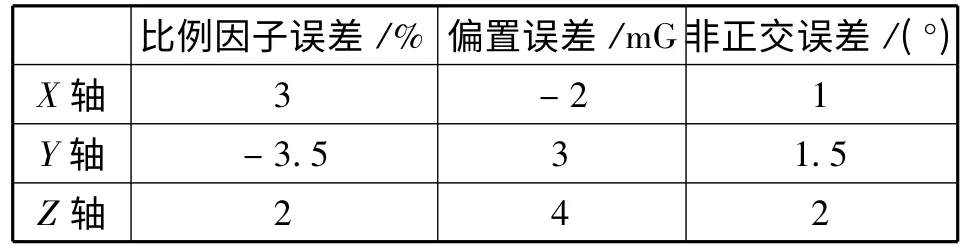
表1 给定原始误差

采用SIMULINK建立仿真模型，如图1所示，当火箭弹转速为10r/s，弹道倾角在50°～0°之间变化时，传感器所测曲线如图2所示。

图1 仿真模型

图2 传感器所测曲线

采用上述算法，识别误差如表2所示。

表2 识别误差

4 结论

综上所述，使用这种新型的三轴磁传感器误差校准算法，可以大幅度提高三轴磁传感器校准参数的精度，同时，这种方法也可以提高计算速率，降低解算难度。尤其对旋转稳定的火箭弹的参数校准提供了很大便利。所以这种方法为更加实时精确的测量弹体姿态数据提供了可靠依据。

[1]刘宗尧，黄学功.三轴磁阻传感器误差补偿方法研究[J].弾箭与制导学报，2011，31(1):241 －243.

[2]闫辉，肖昌汉，张朝阳.三分量磁强计水平校正方法[J].电子测量与仪器学报，2006，20(16):90－93.

[3]Alonso R，Shuster MD. Complete linear attitude－independent magnetometer calibration[J]. Astronautical Sciences，2002，50(4):477 －490.

[4]林春生，向前，龚沈光.三轴磁强计正交误差分析与校正[J].探测与控制学报，2005(6):9－12.

[5]Kim E，Bang H，Lee S－H. Attitude－independent magnetometer calibration considering magnetic torquer coupling effect[J]. Journal of Spacecraft and Rockets ，2011，48(4):691–694.

[6]王正林，刘明.精通 MATLAB 7[M].北京:电子工业出版社，2006.