射流元件延迟时间对滚转火箭弹控制精度影响*
2013-12-10马武举
马武举,夏 青
(中船重工第710研究所,湖北宜昌 443003)
0 引言
精确打击是现代武器装备发展的方向,因此为提高射击精度,旋转火箭弹由无控改为采用简易控制技术的有控火箭弹。射流执行机构是对旋转火箭弹进行弹道修正或姿态控制常用的执行机构。当旋转火箭弹使用射流执行机构进行弹道修正或姿态控制时。射流执行机构在接到控制信号到产生控制力有一定的延迟时间,因为延迟时间的存在,控制系统需要提前某角度发出控制信号,使射流执行机构在需要修正力的位置上产生控制力。为了给弹体在准确方位施加控制力,弹体控制系统都需要确定执行机构的延迟时间,从而确定相位超前角。因此分析制导滚转火箭执行机构动态特性,对于制导滚转火箭精确控制有重要作用。
文中以射流元件控制的滚转火箭为研究对象,进行了射流元件等效控制力及模型分析。研究了射流力切换延迟时间与指令相位超前角的关系,并且对传统的固定指令相位超前角和实时指令相位超前角进行了带射流执行机构动态特性的六自由度仿真,为提高滚转火箭的控制精度提供了重要参考。
1 射流元件执行机构
1.1 射流执行机构的工作原理
射流执行机构产生操纵力:靶弹使用射流执行机构进行单通道控制,可同时实现俯仰控制和偏航运动的控制。射流执行机构采用脉宽调制信号直接控制电磁铁从而操作射流执行机构
射流执行机构的工作原理如图1所示,当电磁铁一侧通电时,档板将堵住一个喷嘴,与该喷嘴相通的活塞腔压力升高,档板堵住一个喷嘴的同时,放开另一个喷嘴,与被放开的喷嘴相通的活塞腔压力降低,活塞两侧产生压力差,当该压力差产生的力大到可以克服摇臂阻力时,活塞带动摇臂运动,直至摇臂将一个主喷口堵住,另一个主喷口完全打开并产生射流控制力。当双向电磁铁另一侧通电时,气流从另一个主喷口流出,产生相反方向的控制射流力。

图1 射流元件工作原理示意图
由于弹体本身具有低通滤波特性,故只有射流执行机构产生的操纵力的周期平均值才能得到弹体的响应。假设弹体滚转时,射流执行机构处于水平位置。操纵力随弹体滚转,若控制信号的极性不变,则操纵力随弹体滚转一周在准弹体坐标系中Oy4轴和Oz4轴的周期平均操作力为零。若弹体滚转前半周期控制信号极性和后半周期控制信号极性相反,则操纵力为随弹体滚转一周在Oy4轴和Oz4轴上的投影变化曲线的积分。

式中:F为射流执行机构产生的瞬时射流力。其作用在弹上的周期平均操纵力为:

也就是说,当控制信号的初始相位为零时,弹体每滚转半周,控制信号改变一次极性,于是作用于导弹上的周期平均操纵力与Oy4轴方向重合。若控制信号的初始相位超前(滞后)某个滚转角度γ0,那么周期平均操纵力也将超前(滞后)滚转角度γ0。这时周期平均操纵力在准弹体坐标系Oy4轴和Oz4轴方向上的投影分别为:
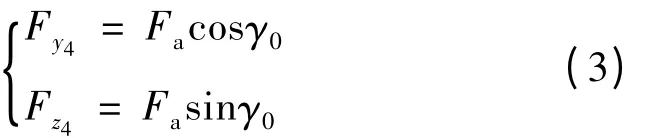
1.2 射流力切换延迟时间
由射流元件的工作原理可知,在射流执行机构中增加传感器以测试活塞的位置,可间接获得射流力切换的延迟时间。图2~图4为射流力切换延迟测试结果。图2为射流力与活塞位置之间的关系,由于动态射流力测试时产生很大震荡,测试结果耦合很大干扰。

图2 推力与活塞位置关系曲线

图3 控制信号与活塞位置信号曲线
测试结果显示活塞位置与射流力切换具有较好的一致性,可用活塞位置曲线变化近似表征动态力切换时间。图3中,活塞位置信号相对控制信号的相位延迟即为射流力的切换延迟时间。
由于燃气压力在初期和末段并不稳定,这直接影响射流元件射流力切换延迟时间。图4为射流元件全工作过程中的延迟时间,射流力切换延迟时间离散分布在10~30ms之间。
为便于分析,将射流元件数学模型简化为一阶非线性惯性环节。
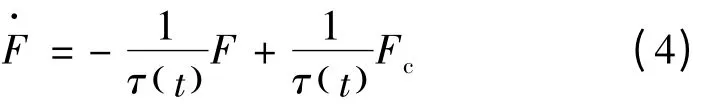

图4 燃气试验射流元件延迟时间
其中:Fc为射流执行机构产生的瞬时射流力;τ(t)为射流力切换延迟时间,其为时间的函数,如图4所示。
2 考虑射流元件特性动力学模型
基于射流执行机构控制滚转火箭的动力学特点,考虑等效控制力和时间控制指令之间的转化关系,可得到滚转火箭弹完整的动力学模型。
在弹道坐标系内的质心运动力学方程:

弹体坐标系内建立扰质心转动的动力学方程:

在地面坐标系中的运动方程:

地面坐标系建立绕质心运动学模型:
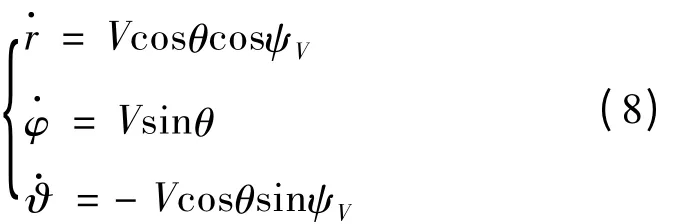
几何关系方程:
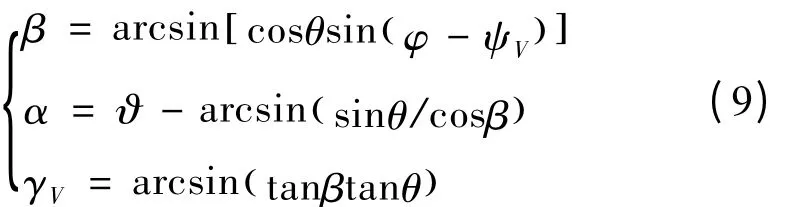
忽略推力的影响,仅考虑气动力及气动力矩以及等效控制力表示的力与力矩表达式为:
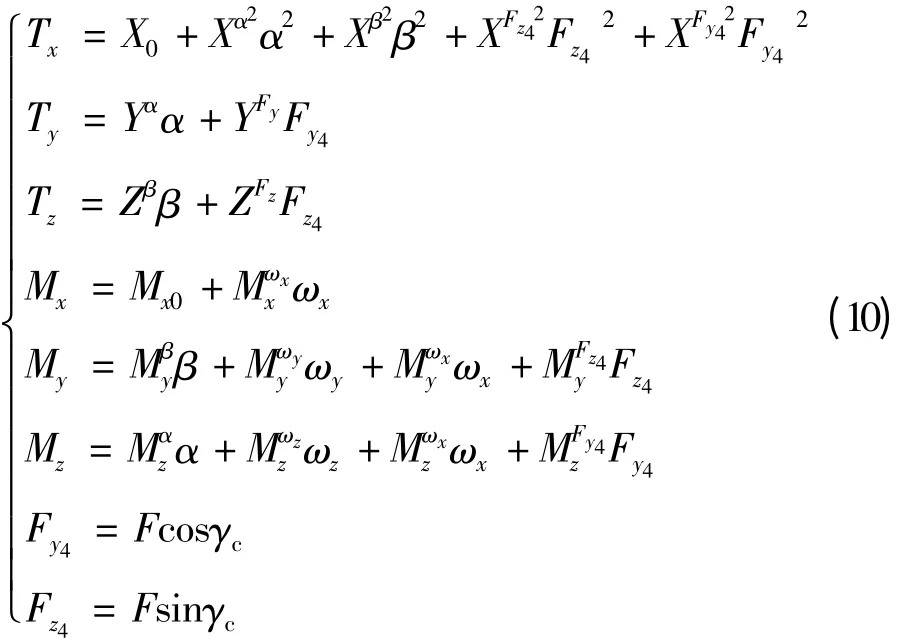
射流元件动力学方程:

式与式构成了射流元件控制力转换,射流元件方程及炮弹动力学模型的完整火箭弹运动方程组。式中:Fc和γc为射流元件指令。其它符号见文献[2],由于研究对象采用尾翼斜置使弹体绕纵轴旋转。因此研究中不考虑滚转通道的控制,气动参数主要随速度变化
3 仿真分析
为了分析射流元件时间常数对滚转火箭命中精度的影响,在不考虑其它影响因素时,对炮弹制导控制系统进行仿真。仿真框如图5所示。

图5 射流元件指令形成和传输过程
在仿真过程中,由制导控制系统给出所需要的等效控制力,然后根据式进行射流指令的转换,得出实际射流元件控制力Fc和超前(滞后)角度γc,将其输入到射流元件动力学方程,得出射流元件实际控制力和角度。以不考虑射流元件特性的最终落点为参考点。弹道修正时间为被动飞行段即第80~100s之间对弹道进行控制。理想弹道由于滚转的马格努斯力,使弹道稍稍偏离发射垂面如图6所示。

图6 弹道修正偏航曲线
在第80~100s的被动飞行段内,弹体转速在12~15r/s之间变化,采用固定补偿角时,取射流力切换平均延迟时间为10ms,即固定相位超前角取 γ'=45°。实时超前角为γ'=ωx4·τ(t),其中ωx4为实时测得的弹体转速。偏航弹道修正和火箭修正后的落点分别如图7所示。由图可以看出,固定超前角和实时设定超前角均对受扰弹道有显著的修正作用,与固定超前角相比,变超前角无论是在偏航和射向上均有更精确的控制效果。

图7 弹道修正落点位置
4 结论
文中介绍了一种新型的直接力控制执行机构射流元件,给出了一种实时测试射流力切换延迟的方法。在考虑等效控制力,弹上实际射流元件动力学关系的基础上,建立了滚转火箭的动力学方程。通过六自由度仿真,分析了射流延迟时间对滚转火箭精度的影响。与传统输入指令固定的相位超前角相比,实时动态设置相位超前角能够显著提高命中精度。该研究为改善滚转火箭控制精度提供重要途径。
[1]Wuju-Ma,Xiaoxian-Yao,Jianwei-Cheng. The switch time simulation of a kind of jet element and its effect on control precision[C]//International Conference on Intelligent Computation Technology and Automation,2010:1013-1016.
[2]钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2000.
[3]吴甲生,雷娟棉.制导兵器气动布局与气动特性[M].北京:国防工业出版社,2008.
[4]王旭刚,王中原.弹体滚转和舵机时间常数对炮弹制导精度的影响[J].南京理工大学学报:自然科学版,2011,35(2):182-186.
[5]Zenghui Peng,Xiaodong Song. Modeling and optimization of a kind of Jet element[C]//The 2nd International Symposium on System and Control in Aerospace and Astronautics,2008:1-4.
