一种基于DSP和FPGA的自适应模版匹配跟踪系统设计*

游培寒，胡 瑜，盛 平，2，王志民

(1 95856部队，南京 210000;2 94921部队，福建晋江 362200;3南京理工大学，南京 210094)

0 引言

模版匹配和目标跟踪是视频图像实时处理中的难点问题，以往系统设计中，由于器件的运算速度有限，不能够做到大规模的模版匹配和大范围的搜索运算。而完全依赖金字塔等算法对模版进行压缩又会丢失大量信息[1]，造成匹配精度不高和跟踪不稳定，多处理器工作方式是实时视频处理系统设计的唯一解决方法。但是以往设计中，大量系统资源被用于总线控制和系统间数据传输，影响了系统性能的发挥[2]。文中设计了一套基于 DSP和 FPGA的图像模版匹配和自动跟踪系统。DSP主要负责图像数据的传输和控制，并预处理匹配模板和匹配数据;而FPGA完成模版匹配并将目标位置信息传递回DSP。由于模版匹配和图像处理过程相对独立，避免了图像的迟滞。

1 硬件设计

硬件系统结构如图1所示，它主要由一枚TMS320DM642(简称 DM642)和一枚 EP3C25F324C7组成。DM642内置有完整的视频控制模块，它通过I2C设置解码芯片 TVP5150和编码芯片 SAA7121，以27MHz的速度接收 TVP5150输出的符合ITU656标准的数字视频，并将其传递到HY57V28320中的采样图像内存区，完成图像处理过程后，采样图像被拷贝到显示内存区，以标准视频方式传递给编码芯片SAA7121。DSP在进行视频流控制的同时，也将匹配区域数据和匹配模版进行预处理后通过EMIF端口传递给FPGA的内存区域，匹配过程由FPGA内部状态机控制。

图1 系统硬件结构

2 接口设计

DSP与FPGA通信是系统设计的关键。首先将DSP的EMIF端口CE2寻址空间设置为8bit的同步读写接口，再利用IP核在FPGA内部配置出匹配模板和匹配区域的双端口存储区域。其硬件连接关系如图2所示。

图2 硬件连接关系

在设计DSP和FPGA的通信接口时，应注意以下几点:

1)由于EMIF端口是64位的，它的位选信号应取反后接入到FPGA双端口存储区相应的位选端口上[3]。

2)EMIF端口的通信时钟为133MHz，在 PCB布线时应尽量满足等长。

3)线路中的延迟时间不同，CLK接入FPGA后，应利用片上的PLL模块建立锁相电路，调整时钟相位避免通信误码。

4)利用CPLD建立正确的启动和复位顺序，避免DM642和FPGA之间的相互干扰。一般DM642先启动，FPGA后启动。

3 软件设计

3.1 算法分工

虽然模版匹配是一种稳定的图像跟踪算法，但它只能通过修正模板的方式实现图像的旋转、缩放，这耗费了大量的系统资源。文中将预处理模板数据和模板匹配分割为两个过程，如图3所示。

1)利用DSP预处理模板数据:对目标区域进行滤波，去除噪声[4]，然后计算目标区域的梯度图像作为原始模板，再根据原始模板计算放大模版、右旋转模版、左旋转模版，并将生成的模板通过EMIF端口传输给FPGA。

2)利用FPGA进行模板匹配:由于FPGA的并行处理机制，可以同时对原始模板、放大和旋转后的模版进行匹配，寻找最佳匹配结果，用来确定目标位置。当匹配最优点产生在放大模板或左右旋转模板中时，说明目标状态发生了变化，需要重新定义，这时FPGA通过模板更新标志位给DSP一个信号，DSP将重新计算模板数据。

3.2 放大与旋转

3.2.1 放大公式

图像的放大和旋转在DSP内部完成。设放大后像素坐标为(xs，ys)，放大关系如下[5]:

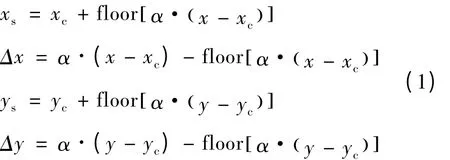
式中:(xc，yc)是放大中心，floor[]是取整函数。放大倍数α选择直接影响算法的稳定性。放大倍数越大，放大的速度越快系统跟踪越稳定;放大倍数小则在放大速度慢时系统稳定。由于文中设计的实际需要，这里设 α =1.1。

双线性插值是一种比较常见的图像缩放计算公式，它既可以避免图像的畸变，同时计算量又相对较少，比较适合本系统应用。

图3 软件结构

3.2.2 旋转公式

设旋转后的坐标为(xs，ys)，设:要更新匹配模板，设置更新模板标志位。在复位状态下，FPGA将清空全部匹配数据。

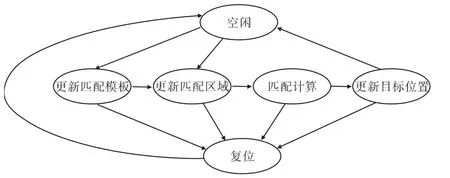
图4 FPGA状态机

3.3 FPGA的状态机设计

FPGA的工作状态可分为更新模板区域、更新匹配区域、匹配计算、更新目标位置、空闲和重启6个状态，其状态机如图4所示。系统处在空闲状态时，根据DSP给FPGA的指令信号FPGA可以进入更新匹配区域或更新匹配模板状态，更新匹配区域后FPGA自动进入匹配计算状态，匹配计算主要完成(x，y)位置ρ(x，y)2的计算，更新目标位置状态主要计算新的目标位置，同时根据最优点所对应的模板，判断是否需

3.4 匹配计算及其优化

文中采用的匹配准则如下[6]:

其中:(x，y)代表匹配位置，(x'，y')代表匹配区域N×M大小的邻域坐标，p(x'，y')是匹配区域像素，t(x'，y')是模板像素，p－是匹配区域像素均值;式(4)对于图像的灰度线性畸变具有不变性，稳定性较好，但直接引用式(4)，无法在FPGA中实现，将式(4)做了如下调整:

在FPGA中的计算时序如图5所示。

图5 ρ(x，y)2的优化前的计算时序

通过图5可以发现，计算ρ(x，y)2需要14个乘法器，占用时间主要集中在第一步，需要 (N×M+6)个时钟周期。第二步和第三步所需时钟周期总共为16个，而第二步中3个乘法和减法器在结构上有类似之处，可以简化为一个乘法与减法器，适当增加第二步所耗费的时钟周期对整个计算过程不会造成过高影响。利用一个时序状态机优化系统结构如图6所示。

图6 ρ(x，y)2的优化后的计算时序

优化后的ρ(x，y)2的计算需要占用FPGA中11个乘法器，如果同时比较旋转和缩放模板，需要44个乘法器，不到文中选用芯片内部乘法器资源的一半。优化后的 ρ(x，y)2计算需要 (N×M+38)个时钟周期。

3.5 更新目标位置

单个ρ(x，y)2计算完成后将其存储在FPGA制定缓存中，更新坐标(x，y)，得到匹配区域中所有子空间对应的 ρ(x，y)2，最大 ρ(x，y)2所对应位置就是目标新坐标，当其对应的匹配模板不是原始模板，则设置更新匹配模板标志位为1。DSP的图像处理周期与FPGA的计算周期存在时间差。为了避免DSP读取非法数据，在FPGA中设置一个双向目标位置地址，该地址内数据保留了目标当前位置和模板更新标志位。FPGA匹配计算结束后，会更新地址内的目标位置和模板更新标志。DSP在每个处理周期都会读取该地址内的目标位置和模板更新位。这样做可以保证DSP每次读取的都是最新的目标匹配计算结果。

4 实验数据

文中设计的自适应模版匹配跟踪系统硬件平台如图7所示。利用SDZ310相机作为成像器件，对跟踪系统性能进行了跟踪能力和计算速度测试。

图7 视频跟踪系统

4.1 跟踪能力测试

利用SignalTAPII记录FPGA部分数据，得到静态图像测试结果如表1、表2所示。

参考国内某型红外成像导引头跟踪器指标，对跟踪器动态跟踪性能进行了测试:将摄像机架设在云台上，对不同灰度反差、放大倍数的移动平面目标进行旋转跟踪。试验结果如表3～表7所示。表中√表示目标在视场移动速度小于8像素每秒时，跟踪器能够稳定跟踪目标，没有丢失目标或跟踪点大幅度抖动现象。通过表3～表7可以看出，跟踪器能够满足目标视在灰度反差6%，旋转速度小于20°/s，缩放速度小于2.0倍 /s的移动平面目标稳定跟踪要求。

4.2 计算速度测试

由于模版匹配计算与视频通道隔离，系统跟踪计算并不会迟滞视频显示时间，系统图像处理速度可以稳定在每秒25帧。同时由于采用FPGA完成并行计算，其可处理的模板面积较大，计算速度较快。跟踪速度测算与实测结果如表8所示。可以看出，当模板面积为128×128像素时，系统每秒仍能跟踪28帧图像。

5 结束语

文中设计了一套基于模板匹配的视频跟踪系统。该系统硬件采用DSP+FPGA结构，DSP负责图像的缓存，并负责模板数据计算，FPGA负责匹配准则的计算和最佳匹配位置的确定等。文中给出的跟踪系统的试验测试结果表明，系统能够满足当目标旋转、缩放等条件下的跟踪要求，同时处理速度可以满足128×128像素的大面积模板跟踪需要。

表1 当匹配图像发生6°偏转时的部分计算结果

表2 当匹配区域发生放大1.1倍时的部分计算结果

表3 视在灰度反差不同目标跟踪结果

表4 视在灰度反差为20%的目标缩放跟踪结果(画面从15倍放大到30倍)

表5 视在灰度反差为15%的目标缩放跟踪结果(画面从15倍放大到30倍)

表6 视在灰度反差为20%的目标旋转跟踪结果

表7 视在灰度反差为15%的目标旋转跟踪结果

表8 跟踪速度测算与实测结果

[1]Luigi Di Stefano，Stefano Mattoccia. Fast template matching using bounded partial correlation[J]. Machine Vision and Applications，2003，13:213 －221.

[2]Xu Xiaoshen，Jiang Hongxu，Jin Liang，et al. A Multi-DSP system for high-performance video applications[C]//11th IEEE Singapore International Conference on Communication Systems，2008:778 － 782.

[3]Altera. Cyclone III handbook Volume 1，San Jose，CA 95134[M/OL]. 2003.

[4]McDonnell MJ. Box-filtering techniques[J]. Computer Graph Image Process，1981，17(1):65 －70.

[5]Aokage H，Wada K，Toraichi K.High quality conversion of image resolution using two-dimensional sampling function[C]//Communications，Computers and Signal Processing，2003.PACRIM. IEEE Pacific Rim Conference on，Vol.2，2003:720 －723.

[6]Zuxun Zhang，Jianqing Zhang. Digital Photogrammtry[M].Wuhan Publishing，1997.