摩擦摆基础滑移隔震框架结构理论研究

何志坚，王社良

(西安建筑科技大学 土木工程学院，西安 710055)

摩擦摆系统最早由Zayas提出，特有的圆弧滑动面使其具有自限、复位机制和振动稳定性，易于工程实现。摩擦摆隔震的理论研究日臻完善。广州大学龚健等人推导了摩擦摆支座的刚度和等效粘滞阻尼比[1]。但是，摩擦摆基础滑移隔震用于多层钢筋混凝土框架结构的数值模拟不多。本文采用有限元结构分析与设计软件SAP 2000对摩擦摆基础滑移隔震框架结构进行数值模拟分析。

1 工程概况

研究对象为一座首层高4.2 m,其余各层高为3.6 m的5层现浇钢筋混凝土框架结构，X方向2跨，轴间距为3 m；Y方向2跨，轴间距为3 m；抗震设防烈度为7度，地震加速度为0.1 g，地震分组为第一组，框架等级为二级，地面粗糙度为B类。结构阻尼比为0.05，混凝土强度为C 30。底层柱截面750 mm×750 mm，其余各层柱截面600 mm×600 mm，主梁截面为300 mm×600 mm，次梁截面为200 mm×400 mm。屋面板厚度为200 mm，楼板厚度为150 mm。楼面恒荷载为5 kN/m2，活荷载为2 kN/m2；屋面恒荷载为7 kN/m2、活荷载为2 kN/m2；梁间均布线荷载为10 kN/m。重力荷载代表值100%（恒荷载+自重）+50%活荷载。梁柱配筋按SAP2000中默认的最小配筋率要求配置。现浇钢筋混凝土框架结构，主梁和次梁的搭接点是刚接点。结构平面图、1－1剖面图和有限元模型立体图分别见图1、图2和图3。

2 SAP2000分析的基本过程

在SAP2000中生成一个完整的分析过程大致分为模型建立、工况定义、模型分析和数据提取。下面简要介绍生成典型模型的基本过程。

图1 结构平面图Fig.1 Structure plan

图2 1－1剖面图Fig.2 1-1 section

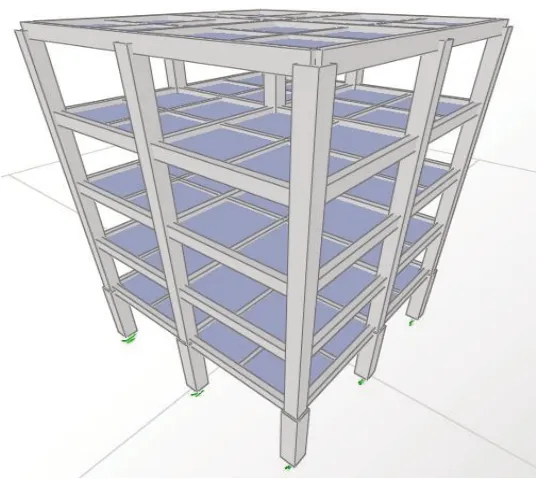
图3 有限元模型立体图Fig.3 Finite element model drawing

模型建立：设置单位→定义轴网，编制轴网→定义材料属性→定义梁柱截面、面截面属性→绘制梁柱→动框架剖分→绘制楼板、屋面板→面网格划分定义荷载模式→定义荷载组合→指定框架重力荷载→添加面恒、活荷载→添加梁间线荷载→定义隔震支座→绘制支座；

工况定义：定义质量源→定义模态工况→定义地震波时程函数；

模型分析和数据提取：运行分析→定义组→指定组→截面切割→显示表格→导出到excel表格。

3 隔震层的模拟

3.1 摩擦摆支座的计算模型

图4是摩擦摆支座的受力分析图，可简化为一个沿圆弧面滑道运动的滑块[2]。滑块质量为m，θ是滑块m相对于滑道竖向对称轴运动的转角，取逆时针为正。滑动面与滑块是面接触，在滑动过程中耗散能量，其间可涂有摩擦材料，如聚四氟乙烯。摩擦摆支座由于其特殊的几何构造而具有位移复原能力。当地震作用力超过静摩擦力时，地面的水平运动会促使滑块在其圆弧面内水平滑动，会让上部结构轻微抬高。然后，滑块又会在自身重力作用下恢复到原来位置，至圆弧活动面最底部。

图4 摩擦摆支座计算模型示意图Fig.4 Friction pendulum bearing calculation model schemes

图中，支座承受的竖向荷载为W，滑道半径及滑块底部圆弧面半径均为R。当滑块在转角θ处时，其水平位移xb=Rsinθ，所受正压力N=Wcosθ，所受到的滑动摩擦力f=μNsgn(x˙b)，滑动摩擦因数为μ，sgn(x˙b)是符号函数

由滑块的受力平衡，对O点取距，∑MO=0，[3]得到

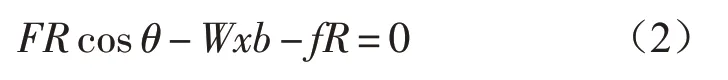
于是，摩擦摆隔震支座的水平力F，亦为基底剪力，可表示为“回复力”和“摩擦力”之和：

当滑块转角θ很小时，cosθ的值接近1，式（3）可简化为：

由式（4）可知，摩擦摆隔震支座的侧向摆动刚度为

3.2 等效刚度和自振周期

设摩擦摆隔震结构的上部结构刚度为Ks，与隔震支座的刚度串联后，隔震系统的等效刚度为

若上部结构为刚性结构，则刚度Ks→∞。对于隔震结构，一般

因此，摩擦摆隔震结构的等效自振周期为

由式（8）说明，摩擦摆隔震结构的自振周期仅与滑动面球面半径R，摩擦因数u和支座设计位移Dd有关，而与上部结构的质量无关，因此具有良好的稳定性。若从最大控制残余位移方面考虑，必有μR=Dd，于是式（8）可简化为

3.3 SAP 2000中的摩擦隔震单元

选用SAP 2000中的Friction isolator连接单元来模拟结构中的摩擦摆滑移隔震装置。把该连接单元布置在首层各框架柱下。该单元是一个双轴摩擦摆隔震单元[1]，可模拟在接触面上的摩擦行为。对于每个剪切变形自由度，可独立指定为线性或非线性。该单元中，摩擦力和单元的轴压力成比例，单元的轴力总是非线性的。U1代表支座的Z方向，U2和U3分别代表X、Y方向。本文考虑非线性分析工况的作用，模拟滑移隔震元件时U1方向要定义为非线性属性，是支座承受竖向荷载的方向，承受足够大的竖向荷载，所以一般取其刚度值为较大值。U2和U3为两个水平方向，U2和U3方向支座参数的取值相同。

3.4 摩擦摆支座的参数设计

3.4.1 定义荷载工况结果组合

定义荷载工况结果组合用于求解结构所受到的内力。定义荷载组合采用默认设计组合，混凝土框架设计。用基本的三种组合方式进行荷载组合，取最大值作为设计值，按最不利荷载情况去计算。

3.4.2 模态分析中质量源的定义

1）楼面恒荷载为5 kN/m2，屋面恒荷载为7 kN/m2；

4）指定框架重力荷载模式：DEAD；重力乘数全局Z=-1；替换或添加到现有荷载。

3.4.3 摩擦摆支座的几个主要参数

隔震层是隔震结构的重点部位，直接影响到隔震效果。在对摩擦摆支座进行设计时，几个主要参数的物理意义如下：Ki为支座的初始刚度或非线性刚度[4]，由式(10)计算；其中，Dy表示支座屈服时的位移，Dd为支座的极限位移[5]或设计位移

摩擦因数取0.05。取滑道的曲率半径R=1.5 m[5]，设摩擦摆的设计位移为Dd=0.2R=300 mm，屈服位移Dy=2.54 mm。对结构固定支座模型进行模态分析，获取结构首层柱子底部承受的竖向轴力，取最大压力，可得出摩擦摆支座所受的竖向压力W。SAP 2000中F3为竖向受力方向。节点编号69为中柱底部，节点编号2、4、87、93分别为边柱底部，节点编号1、3、92、94分别为角柱底部。节点1、2、3所在的截面为迎地震波的截面。按照等效刚度公式（7）和初始刚度公式（10），可计算出9个摩擦摆支座的线性刚度和非线性刚度。取摩擦因数随速度变化的控制指数为100 m/s[6]。支座压力和刚度如表1所示。其中，N3=N1，N87=N4，N94=N92。可看出，几何规则对称结构的中柱底部所受的竖向压力最大，其次是边柱底部，而角柱底部受到的竖向压力最小。

表1 支座压力(kN)和刚度（kN/m）Tab.1 Bearing pressure(kN)and stiffness(kN/m)

4 荷载工况分析

4.1 模态分析

模态分析也叫振型叠加法动力分析，用于线性结构动力分析。模态分析可得到结构基本动力特性参数，如自振周期、频率和各阶振型。模态分析之前要定义质量源。通过模态分析，得出隔震结构的第一周期为2.454 s。而根据公式（9）计算出T=2.457 s。程序分析值与公式计算值非常接近，吻合。说明建模和摩擦摆支座参数设计正确。

4.2 时程分析

4.2.1 定义时程函数

采用时程分析法要输入地震波加速度曲线，这里仅考虑单向水平地震作用，选用持时为30 s的N-S向EL-Centro波，代表（Ⅱ）类场地。原始记录离散加速度时间隔为0.02 s，所以等时间间隔值取0.02 s。

4.2.2 快速非线性分析法（FNA）

结构在大震状态(罕遇地震)时部分构件会出现塑性发展，此时需要程序能够进行一定深度的弹塑性分析并给出相应结果。此外，隔震装置一般是用非线性连接单元去模拟，而线性时程分析不能够考虑非线性连接单元的非线性属性。因此，本文隔震结构的分析采用非线性时程分析方法。

SAP 2000程序的Fast Nonlinear Analysis Method(快速非线性分析法)，简称FNA方法，也称非线性振型叠加法，是一种非线性分析的有效方法。摩擦隔震器定义中的U1、U2、U3方向分别代表全局坐标系的Z、X、Y轴，而输入地震波时U1、U2、U3分别代表全局坐标系的X、Y、Z轴。选择U2方向输入地震波。《建筑抗震设计规范》(GB50011—2010)表5.1.2—2中时程分析所用地震加速度时程的最大值规定，7度多遇地震和罕遇地震分别为35 cm/s2和220 cm/s2。由地震波幅值调整公式：

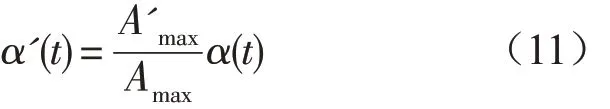
式中，α'(t)、A'max—分别表示调整后的地震加速度与峰值，A'max取《抗规》表5.1.2-2中设防烈度要求的多遇地震及罕遇地震的加速度峰值或与抗震设防烈度相应的设计基本地震加速度值；α(t)、Amax—分别表示原地震记录加速度曲线和峰值。

时程分析中所选用的EL-Centro波的文本格式数据是以gal=cm/s2为单位的，它的峰值为341.7 gal=341.7 cm/s2=341.7×0.01m/s2。而SAP2000的单位用的是kN/m/s,也就是SAP 2000的单位与原始波的单位相差0.01个单位，那么比例系数要输入0.01。规范中的7度多遇要求是35 gal，比例系数应取0.01×（35/341.7）＝1.024×10-3。7度罕遇要求是220 gal，比例系数为0.01×（220/341.7）＝6.438×10-3。考虑到时程函数的等时间间隔值0.02 s，地震波持时30 s。时间步数据为输出时段大小0.02 s，输出时段数1 500。具体的时程分析工况设置如表3所示。

表2 时程分析工况设置Tab.3 Time analysis of the operating mode settings

表3 结构自振周期Tab.3 Structural natural periods

5 隔震效果分析

5.1 自振周期

通过模态分析，模态类型选择特征向量，得到如下结果：

表4是隔震前后结构振动的前三个周期，可看出，摩擦摆结构的周期较非隔震结构的周期有所延长，非隔震结构的主要周期约0.909 s，而滑移隔震结构的主要周期为2.454 s，隔震结构的主要周期为非隔震结构主要周期的2.7倍。非隔震结构的自振周期较短，与场地的卓越周期相近，容易发生共振现象，不利于抗震。而滑移隔震结构的自振周期明显延长，远离场地的特征周期，减小结构发生共振的可能，从而把地震动有效地隔开，降低上部结构的地震反应，也说明摩擦摆隔震结构适宜建在特征周期较短的场地上，它对短周期分量为主的地震波的隔离效果更为明显。

5.2 楼层的加速度反应对比

SAP 2000中的节点相对加速度是指节点相对于结构的加速度，节点绝对加速度是指节点相对于地面的加速度；此处取绝对加速度。非线性时程分析，尽管某一楼层各点加速度的最大值可能发生在不同时刻，这里近似取楼层各点最大绝对加速度值的平均值来代表该楼层的最大加速度反应。为了方便比较，定义减小率=（非隔震结构反应—隔震结构反应）/非隔震结构反应。减小率越大，表示其隔震效果越好，设0层为隔震层。

表5对比了七度多遇地震和罕遇地震作用下非隔震结构与隔震结构各层的最大加速度值，可看出，滑移隔震结构各层最大加速度基本呈“K”型分布，符合理论推导的滑移隔震结构加速度分布趋势。隔震效果非常明显，尤其是3层和顶层。隔震上部结构基本上呈整体水平移动，可以有效地避免大震时上部结构和结构内部设备及装饰发生破坏。

5.3 楼层的层间位移对比

由《高层建筑混凝土结构技术规程》（JGJ3-2010）3.7.3条第3款注，楼层层间最大位移以楼层竖向构件最大的水平位移差计算。模型某两个节点的相对位移输出，可以用广义位移。定义广义位移一般要在模型分析之前进行。本模型楼板是刚性楼板，平面内刚性无穷大。层间位移是同一时刻，不同楼层的位移差，本模型是规则对称结构，可选取相邻楼层的中心点去分析层间位移。

表6对比了七度多遇地震和罕遇地震作用下非隔震结构与滑移隔震结构各层最大层间位移值。可看出，非隔震结构有明显的剪切型变形并且各层最大层间位移相对比较大，而滑移隔震结构的位移主要在隔震支座处，上部结构的各层最大层间位移比较小，基本处于平动状态。

表4 多遇和罕遇地震下各层最大加速度Tab.4 Each layer maximum acceleration in frequently and rarely met earthquake

表5 多遇和罕遇地震下各层最大层间位移Tab.5 Each layer maximum displacement in frequently and rarely met earthquake

表6 多遇和罕遇地震下各层最大层间剪力Tab.6 Each layer maximum shear in frequently and rarely met earthquake

5.4 楼层的层间剪力对比

对模型某个位置切割面的综合内力输出，可用截面切割，是一种求合力的快捷方法。截面切割及用于截面切割的组的定义不要在手工网格划分之前进行，且建议在分析完成之后进行。表7对比了七度多遇地震烈度和罕遇地震烈度作用下非隔震结构和滑移隔震结构各层最大层间剪力值，多遇地震作用下底层最大层间剪力从444.654 kN减小为110.814 kN；罕遇地震作用下底层最大层间剪力从2 795.591 kN减小为696.701 kN，可见隔震效果非常明显。

6 结语

合理建模和设置隔震层参数，能得到较为理想的摩擦摆基础隔震效果。但这只是结构设计与分析软件程序分析出来的结果，与实际工程的应用会存在差别，差别有多大值得深究。程序分析中隔震层与1层的层间位移仍比较大，如何限制隔震层的位移，做好限位措施的同时又增强隔震效果，仍待如缩尺的模型试验或实际工程应用等的更进一步的深入研究。

[1]北京金土木软件技术有限公司，中国建筑标准设计研究院SAP2000中文版使用指南[M].人民交通出版社，2006，9.

[2]巫 炜.摩擦摆隔震结构分析[J].北京：交通大学，2007.

[3]龚 健，邓雪松，周 云.摩擦摆基础隔震支座理论分析与数值模拟研究[J].防灾减灾工程学报，2010，31（1）：56-62.

[4]胡继友.基于性能的摩擦摆基础隔震结构抗震性能研究[D].郑州大学硕士学位论文，2011.

[5]陈永祁，杨风利，刘 林.摩擦摆隔震桥梁的设计及应用[J].工业建筑，2009，39(S)：256-260.

[6]A.MokhaG A.NavinchandraG M.Constantinou and V.Zayas.Seismic isolation retrofit of large historic buildings.J.Struct.Eng.，1996，122：298-308.