梁损伤小波包分析和神经网络识别

孟范孔，邱志成

（华南理工大学 机械与汽车工程学院，广州 510641）

柔性梁结构振动产生的动应力和动变形会引起结构的疲劳与损伤。从而使结构承受正常载荷以及环境作用的能力下降，引发突发性的灾难事故[1]。因此，需进行损伤识别研究。

小波分析具有多分辨率的特点，在损伤识别领域有广泛的应用。Rucka等[2]利用小波分析可以检测信号奇异性的原理对梁、板的损伤进行识别。Yan等[3]和丁幼亮等[4]利用结构动力响应的小波包能量谱建立损伤识别指标。BP神经网络是进行结构损伤识别的有效方法，Liu等用BP网络识别框架结构的损伤[5]。米江等将改进的BP网络用于风机故障分类[6]。Ceravolo等[7]先用一个BP网络确定简支梁损伤的程度，再根据特定的损伤程度确定第二个BP网络的训练样本，用于确定损伤位置。

本文用有限元法(FEM)建立柔性悬臂梁系统的动力学方程，并求得状态空间方程用于进行结构动力响应仿真。用小波包对柔性悬臂梁无损伤和有损伤状态下的动力响应信号进行分解，计算小波包节点子信号能量，建立损伤指标。采用分步识别方法和改进的BP神经网络进行损伤位置和程度识别，并进行了数值仿真研究。

1 有限元模型的建立

对梁裂缝进行分析的模型有局部刚度降低模型、精细网格模型等[8]。文中用精细网格模型对梁的裂缝进行分析。

用每节点三个自由度的四节点矩形板单元，对悬臂梁进行离散化。悬臂梁经网格划分后共n个节点，激励为作用在梁上一节点的z方向的集中力，输出为柔性梁上一节点的加速度响应。有限元法建立的动力学方程为

式中M∈R3n×3n、C∈R3n×3n、K∈R3n×3n分别是整体质量矩阵、阻尼矩阵和刚度矩阵，并且C=αM+βK，α，β为 阻 尼 系 数 。d∈R3n×1、∈R3n×1、¨∈R3n×1分别为整体节点位移向量、节点速度向量、节点加速度向量。u(t)为激励力，Fext∈R3n×1是与激励力作用位置有关的向量。

所要观测节点的加速度输出

式中T∈R1×3n为观测矩阵。

式(1)、(2)经模态坐标变换d=Φg得

式中g为模态坐标，Φ=M-1K为模态矩阵。

式(3)、(4)经变换得

式中

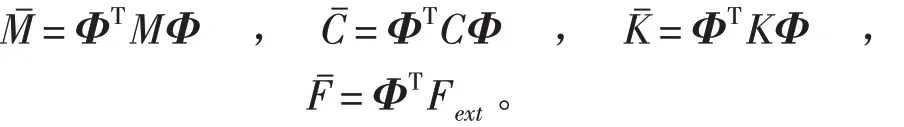
式(5)、(6)表示为标准的状态空间方程形式

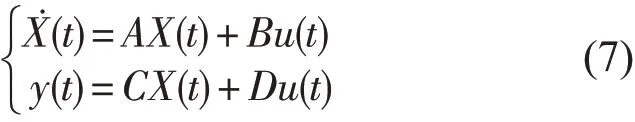
式中X(t)为状态向量，y(t)为加速度输出，A、B、C、D分别为系统矩阵、控制矩阵、输出矩阵和直接传递矩阵，u(t)为外部激励力。并且

2 损伤识别算法

2.1 基于小波包分解的损伤指标

结构发生损伤时，结构的动态特性会发生改变。用含不同频率成分的信号对结构进行激励时，损伤导致结构对某些频率信号起着抑制作用，而对另外一些频率信号起着增强作用。损伤结构的输出与无损伤结构的输出相比，相同频带内信号的能量会有差异[3,4]。

用S0(t)表示结构的加速度响应信号，则经小波包分解后，S0(t)可以表示为[3]

式中i为小波包分解的层数，Si,j(t)是小波包分解树节点[i，j]的系数重构后的子频带信号。定义第j个子频带信号的能量为[3]

用小波包能量谱中各子频带能量相对于全部频带能量平均值的比值的变化来表征损伤。小波包能量谱中各子频带的能量比Rk为[4]

子频带的能量比表征了结构的动态特性。基于文献[3]的思想，用各子频带能量比的相对变化率作为损伤指标判断结构的损伤情况，即

式中ERVk为小波包分解第k个子频带的能量比相对变化率；Ruk和Rdk分别为结构在无损伤和有损伤状态下第k个子频带的能量比。

2.2 基于BP神经网络的损伤识别

用BP神经网络进行损伤识别。因为标准BP算法存在收敛速度慢、容易陷入局部最小等问题，所以采用加入动量项和学习率自适应调整相结合的方法对BP神经网络进行改进[6]。

加入动量项后下一次迭代时的参数值为

式中W为需要调整的网络参数，ΔW为网络参数的修正量，t表示迭代次数，α为动量因子。

自适应调整学习率算法为

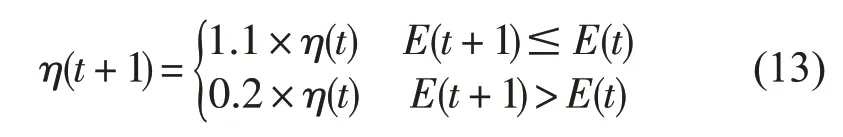
式中，η为学习率，E为全部训练样本的均方误差。设定最大学习率为0.8，最小学习率为0.01。

3 数值算例分析

3.1 问题描述

以柔性悬臂梁为研究对象进行数值仿真。其物理参数如下：长度、宽度和厚度分别为0.656 m，0.165 m和0.002 m；密度为1 865 kg/m3；杨氏模量为34.64 GPa；泊松比为0.33。

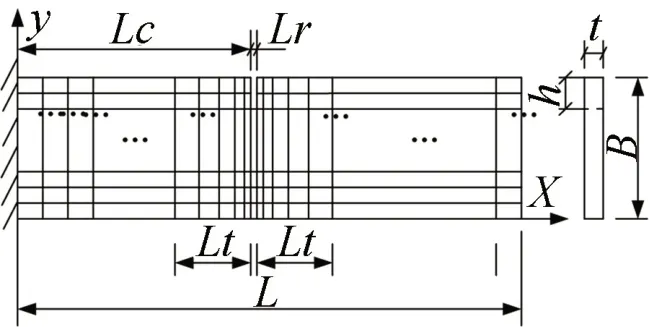
图1悬臂梁示意图Fig.1 Schematic diagram of cantilever beam

图1 所示为悬臂梁模型示意图，裂缝与固定端的距离为Lc，裂缝深度为h，裂缝宽度为Lr=0.001 m。算例中集中力的作用位置坐标为xa=0.075 m，ya=0.080 m。输出加速度响应的位置坐标为xs=0.630 m，ys=0.080 m。本算例进行单损伤的损伤位置和损伤程度识别研究。可能的损伤位置有三处，即裂缝与固定端的距离Lc分别为0.115 m、0.215 m和0.315 m。对每个损伤位置分别考虑14种不同的损伤程度，即裂缝深度h分别为0.010 m、0.015 m、……、0.070 m、0.075 m。分别对所选取的三个损伤位置（每个损伤位置14种损伤程度）的42种损伤情况进行分析。选择其中6种损伤情况作为测试样本，其余损伤情况作为训练样本。测试样本如表1所示。

如图1所示，网格划分时，对于x方向，裂缝所在的位置，网格局部加密。裂缝处为一列单元，在裂缝两侧各有一个长度为Lt的过渡区域。过渡区域内有五列单元，其x方向尺寸由裂缝处向两侧分别为0.001 m、0.003 m、0.005 m、0.011 m和0.020 m。其余部分均匀划分为23列单元。对于y方向，每个单元的尺寸均为0.005 m。经网格划分，x方向单元个数为34，y方向单元个数为33。

模态变换矩阵取前两阶，将求得的状态空间方程离散化用于进行动力响应仿真，计算柔性梁在方波激励下的动力响应。方波激励的频率为5 Hz，幅值为10 N。采样频率为200 Hz，仿真时间为10 s。

表2所示完好柔性悬臂梁的前两阶模态频率。利用模型编程计算值和ANSYS软件分析比较可知，用Matlab计算结果满足精度要求。

3.2 损伤指标的计算

用Db 8小波基函数对获得的加速度响应进行6层小波包分解，得到64个子频带信号。经计算，全部样本的加速度响应信号经小波包分解后，前32个子频带信号的能量占全部64个频带信号总能量的98%以上。前32个子频带的信号能够表征加速度响应信号的主要信息。所以选取前32个子频带信号建立损伤指标。

表1 测试样本Tab.1 Testing samples

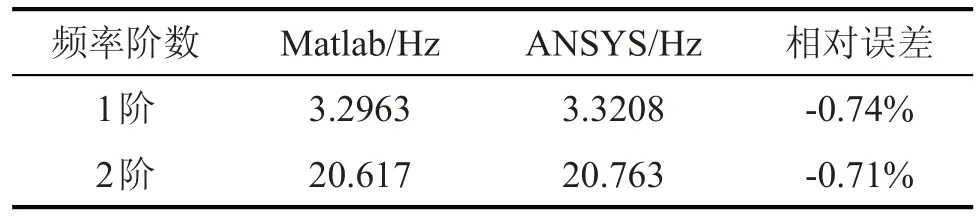
表2 完好梁模态频率Tab.2 Natural frequencies of undamaged beam

图2 测试样本2的损伤指标Fig.2 Damage index of test sample 2

测试样本2的损伤指标如图2所示。从图中可以看出，第1、11、15、27四个子频带的能量比相对变化率发生显著的变化。相对变化率分别为-252.28%、-111.65%、-111.20%、-98.42%。对于不同的损伤情况，小波包分解子频带能量比的相对变化率是不同的。

3.3 损伤模式的识别

用分步识别方法进行裂缝损伤识别。先识别损伤发生的位置，然后识别损伤的程度。因此建立两个三层BP神经网络结构。分别为用于识别裂缝发生位置的损伤位置网络(Damage Location Network)和识别裂缝损伤程度的损伤程度网络(Damage Extent Network)。

损伤位置网络输入层、隐含层、输出层的神经元个数分别为32、24和3。期望输出为[1 0 0]、[0 1 0]、[0 0 1]，分别代表裂缝发生的位置为115 mm、215 mm和315 mm。1表示该位置发生损伤，0表示该位置没有损伤。损伤位置网络隐含层和输出层的作用函数为均为Sigmoid函数。损伤程度网络输入层、隐含层、输出层的神经元个数分别为32、12和1。期望输出为裂缝损伤的程度。损伤程度网络隐含层作用函数为Sigmoid函数，输出层作用函数为纯线性函数。两个神经网络的隐含层神经元个数是经过试验确定的。

将损伤指标数据归一化处理，分别用改进的BP算法(Improved BP，IBP)和标准BP算法(BP)对两个神经网络进行训练。损伤位置网络的初始学习率为0.01，动量因子为0.05，层间连接权值和阈值的随机初始化范围为(-1，1)。误差性能指标为0.01，最大训练次数为10000。损伤程度网络的初始学习率为0.01，动量因子为0.5，层间连接权值和阈值的初始化范围为(-0.1，0.1)。误差性能指标为1×10-6，最大训练次数为10 000。用标准BP算法进行训练时的学习率为固定值0.01。

图3、图4分别为损伤位置网络和损伤程度网络的误差曲线。由图3、图4可以看出，用改进BP算法进行训练时的误差收敛速度比用标准BP算法快。损伤位置网络用标准BP算法训练10 000次后的均方误差为0.184 1，而用改进BP算法训练9 360次后达到目标误差0.01。损伤程度网络用标准BP算法和改进BP算法训练10 000次后的均方误差分别为3.237 4×10-4、1.785 8×10-5。

测试样本的损伤位置、损伤程度识别结果分别如表3、表4所示。由表4可以看出，损伤位置网络的预测值与实际值较为接近，由网络输出的最大值可以判断损伤发生的位置。由表4可以看出，损伤程度网络预测值与实际值的最大相对误差是-5.5%，识别结果满足精度要求。所以，利用分步识别方法，可以对损伤位置和损伤程度进行识别，并且BP神经网络具有较好的泛化能力。

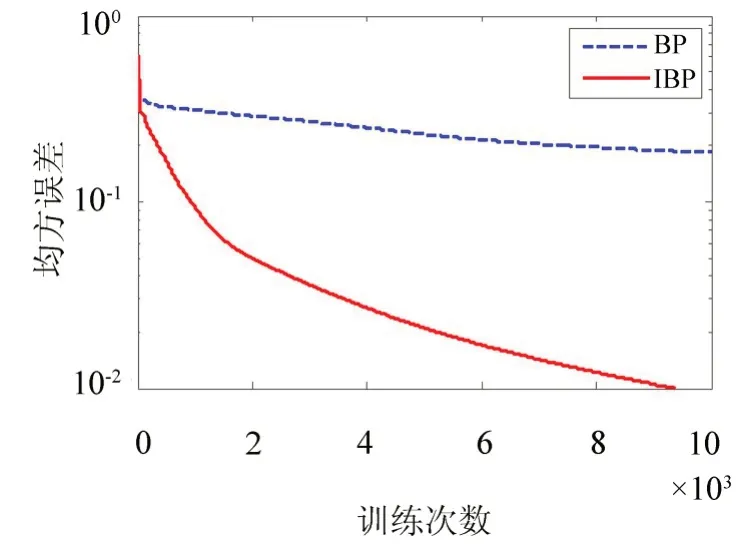
图3 损伤位置网络误差曲线Fig.3 Error curve of damage location network

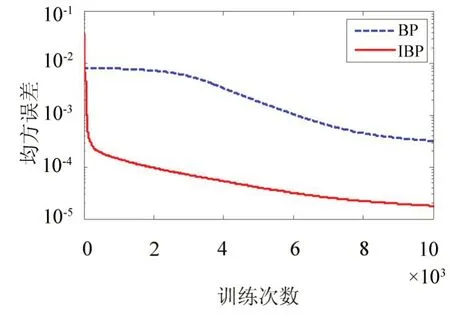
图4 损伤程度网络误差曲线Fig.4 Error curve of damage extent network

表3 损伤位置识别结果Tab.3 Identification results of damage location

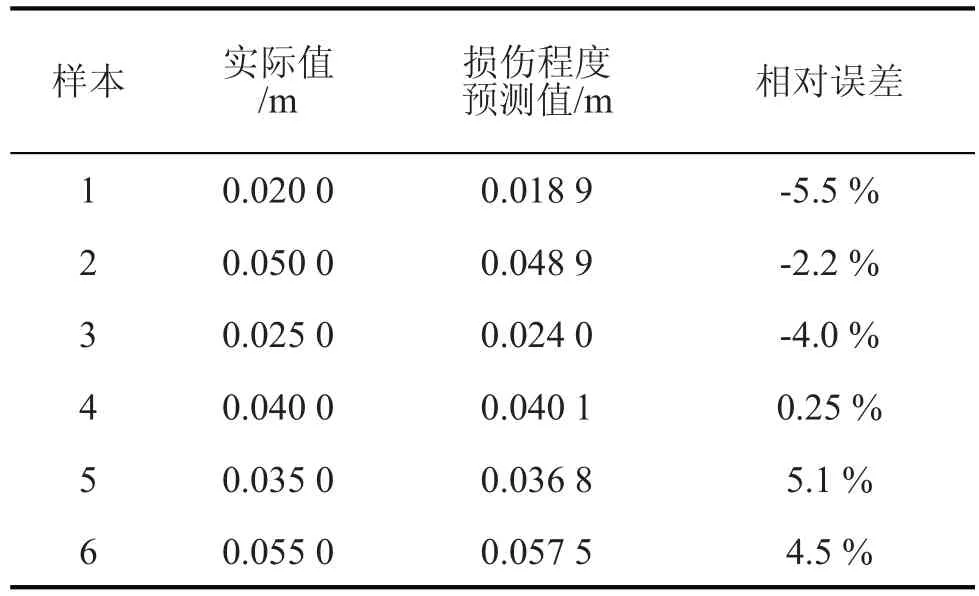
表4 损伤程度识别结果Tab.4 Identification results of damage extent

4 结 语

柔性梁发生裂缝损伤时，结构的动态特性发生改变。利用小波包分析可以对梁的裂缝损伤信息进行提取。基于小波包能量谱建立的子频带能量比相对变化率损伤指标对梁的裂缝损伤敏感。改进的BP神经网络收敛速度快。采用分步识别方法和改进的BP神经网络可以精确的识别出损伤位置和损伤程度。使用小波包分析和神经网络相结合的方法，用低频振动响应就可以实现柔性悬臂梁裂缝损伤位置和程度的识别。

[1]朱宏平，余 璟，张俊兵.结构损伤动力检测与健康监测研究现状与展望[J].工程力学.2011，(28)2：1-12.

[2]Rucka M,Wilde K.Application of continuous wavelet transform in vibration based damage detection method for beams and plates[J].Journal of Sound and Vibration,2006,297(3):536-550.

[3]Yam L H,Yan Y J,Jiang J S.Vibration-based damage detection for composite structures using wavelet transform and neural network identification[J]. Compoossiittee Structtuurreess.2003,60(4):403-412.

[4]丁幼亮，李爱群，缪长青.基于小波包能量谱的结构损伤预警方法研究[J].工程力学，2006，23(8)：41-48.

[5]Liu Y Y,Ju Y F,Duan C D,et al.Structure damage diagnosis using neural network and feature fusion[J].Engineering Applications of Artificial Intelligence,2011,24(1):87-92.

[6]米 江，纪国宜.改进的BP神经网络在风机故障诊断中的应用[J].噪声与振动控制，2011，31(2)：94-98.

[7]Ceravolo R,Stefano A De,Sabia D.Hierarchical use of neural techniques in structural damage recognition[J].Smart Materials and Structures,1995,4(4):270-280.

[8]胡家顺，冯 新， 李 昕等.裂纹梁振动分析和裂纹识别方法的研究[J].振动与冲击，2007，26(11)：146-151.