基于METRIC的民机初始备件数量确定及配置模型

孙 蕾 左洪福

南京航空航天大学，南京，210016

0 引言

一般而言，航空公司的维修部门分为基地和航站两级。基地设有中心仓库，用于内厂维修及支援航站备件。而航站也会适量存储备件，当飞机发生故障时，可以通过快速更换备件，进行离机(off－line)修理，以缩短飞机的停场时间，提高飞机的签派可靠性，避免飞行延误造成巨大损失。

在采购初始备件时，飞机制造商计算推荐数量的模型，仅从基地单一航材的保障水平出发，而航空公司的实际应用表明这种做法的效果非常不理想，备件大量剩余的同时又不能避免停飞待件的情况。其原因是，这种做法割裂了备件故障与飞机可用度的联系，也没有考虑多级库存，缺乏整体的协调与优化。备件库存的目的是维护飞机的正常运行，衡量备件库存水平优劣最好的度量方式是其所保障飞机的可用度，如何以最少的投入获得最大的飞机可用度，才是航空公司在进行采购时最关注的问题。

从20世纪60年代起，国外对多级库存问题进行了大量研究。Sherbrooke［1］在1968年提出的METRIC理论成为后来学者们研究的基础，该理论在建模过程中考虑了维修保障组织的多级结构，但是低估了基地备件短缺量。1985年，Graves［2］提出了 VARI－METRIC 模型的近似算法，同时考虑供应渠道备件数和方差，提高了METRIC模型近似法的精确度，同时还保留了后者适用于复杂系统的优越性。Hillestad［3］提出了Dyna－METRIC模型，考虑了使用需求随时间变化的动态模型。文献［4-5］研究了多级库存中同级库存间的横向供应问题。Kennedy等［6］总结了备件库存问题的研究现状。总之，多级库存理论已经成为提高库存费效比的有效方法，在欧美海军及空军中得到广泛应用。随着我国大飞机项目的启动，国内学者对民机多级库存的研究也越来越多。文献［7-8］通过改变保障指标或优化方法，对多级库存问题进行了积极的探讨。文献［9-10］研究了联合库存情况下的多级库存问题。文献［11-12］对初始备件问题进行了研究，但仅从单级库存角度进行对比，没有考虑多级库存。

本文主要以需求率较低、费用较高，并对飞行安全起关键作用的航线可更换件(line replaceable units，LRU)为研究对象，基于 Vari－METRIC 理论，在(s－1，s)库存策略下，运用边际分析法对波音公司提供的初始备件的数量进行优化，并对两种方案的结果进行了对比分析。

1 问题描述

航空公司的两级维修供应系统由飞机、维修机构、备件库等要素组成，备件在系统中的状态转移流程如图1所示。

图1 两级维修供应流程

当飞机在某航站发现LRU故障时，如果该件是NO GO件，影响飞行安全，则由机务进行定位拆卸。如果航站有备件，则对LRU进行更换，否则发生一次短缺，同时向基地申请LRU备件，此处不考虑航站间的横向备件供应。拆下的故障件在航站进行修理，修好后送回航站对应的备件库;航站无法修的故障件送基地修理，修完后送基地备件库。LRU在上述过程中的状态满足经典库存平衡公式:

其中，s为初始库存量，当库存对策为(s－1，s)时，是一常量;se为现有库存量;nDI为供应渠道件数，是在修理或运输中的备件数;nBO为备件短缺数。式(1)等号右边三个变量都是非负的。所有的s件备件始终处于上述三种状态之一，当nDI＜s时，se大于零，仍有库存。当nDI=s+x时，将会产生数量为x的缺货量，此时考虑nDI＞s时的备件需求分布函数的结果，可得到期望短缺量。

为提高模型工程易用性，作如下假设:①飞机的机型架次均相同;②假设所有LRU的重要程度相同，不考虑设计的冗余性，一旦短缺便导致飞机停飞;③多重故障不同时发生;④航站不维修备件，基地修理能力无限;⑤不考虑串件修理，横向供应。

2 库存建模

客户化的RSPL制定，首先需要客户提供飞机运行的基本规则，如年飞行时间、机队规模、修理周转时间、保障率等。波音公司根据预测模型，分3步求解:①计算年平均需求量;②维修需求量;③计算推荐数量。

2.1 年平均需求量

波音公司的推荐模型中，年平均需求量的计算公式如下:

在METRIC模型中，假设各航站的年平均需求量相同，则有

式中，j为航站标识，j=0，1，…，J，其中0 代表基地，J代表航站数量。

2.2 维修需求量

维修需求量即供应渠道件数μ是修理周转时间(repair turnaround time，RTAT)内发生的备件平均需求量。在波音的推荐模型中，客户通过选择基本规则确定备件的RTAT，客户可以为所有的零件、每个修理码或每个供应商代码分别提供RTAT，对于不同的修理码还需进一步提供主维修时间、辅助维修时间、航站到主基地的返回时间。

为简单起见，本文假设所有备件的RTAT是相同的，由客户规则给出。平均的修理周转时间公式如下:

式中，TRT为航站到基地的往返时间;T为航材在基地的修理时间。

波音维修需求量采用均值等于mTRTAT的泊松分布模拟基地需求，不考虑航站。而METRIC模型将基地和航材需求分开计算，其中基地的期望值为

航站j的供应渠道备件期望值由两部分组成:①运输中的备件;②基地备件短缺而延迟供应航站j的备件。基地对航站的备件申请按先来先到原则服务。所以航站的短缺量等于航站需求占总需求的比例与基地短缺量的乘积，即

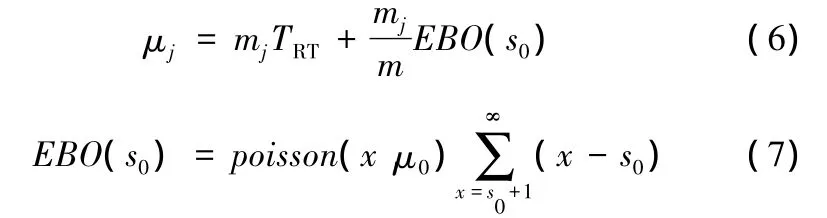
式中，EBO(s0)为基地库存量等于s0时，基地的备件短缺量;poisson(x，μ0)为泊松分布。

由于没有具体的需求数据，所以无法求得方差，此处仍用泊松分布进行模拟。

基地供应渠道备件数的方差为

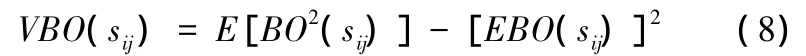
式中，BO为短缺量，等式右边第1项是短缺函数的二阶矩，等式右边第2项是期望短缺函数的平方。

2.3 推荐量计算

波音公司计算推荐量时，假设备件需求满足泊松分布，则当备件为x件时，保障率为

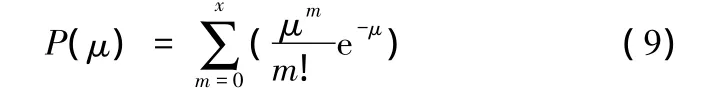
波音公司的公式是针对单一备件分别进行计算的，通过每次加1计算所能得到的保障率，与客户的要求相比，直到满足为止。如，客户要求92% 的保障率，2件备件可达到90%，3件可达到96%，那么将推荐客户购买3件备件。

要应用METRIC模型，首先需要推导机队可用度与总的备件期望短缺量的关系。假设飞机所有备件发生故障的次数相互独立，并且不存在串件维修，则机队中未因任何备件短缺而停飞的飞机架数所占百分比的期望值为

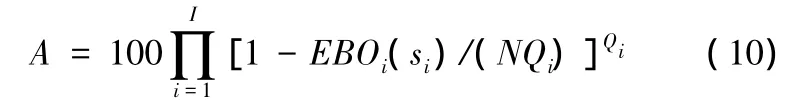
式中，I为备件的品种数;Qi为第i种备件的品种数。

对式(10)两边求对数:

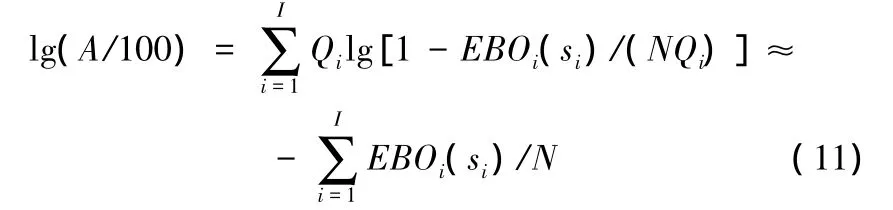
由此可见，最小化机队可用度等同于最大化EBO，综合所有航站所有备件，最优化问题可以归结为以下整数规划:

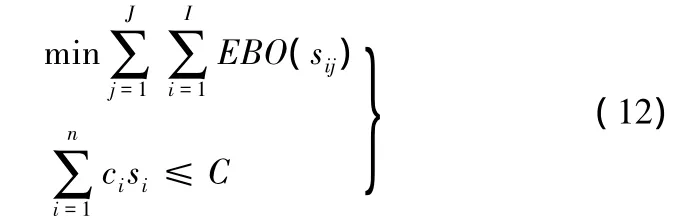
式中，i代表不同的备件。

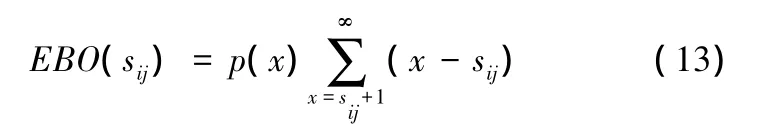
式中，p(x)为需求的概率分布。

航站供应渠道备件数的方差为

根据差均比的不同，参考表1分别选用二项分布、泊松分布和负二项分布中的一种来模拟需求的概率分布。

表1 差均比与概率分布的对应表

3 优化求解流程

目前用于多级库存优化的算法主要有遗传算法和边际分析，前者缺点是多维复杂，仿真速度慢，实际应用困难;后者利用数学模型通过解析法求解，结果可得到可用度与库存投资的转换曲线，而不仅仅是提供一个单独的优化值。虽然其精确性不如前者，但对于飞机这类复杂系统的高效性，使其成功地被商业软件OPUS等采用，并在欧美的海军及空军中得到广泛应用，因此本文也选用边际分析法进行优化求解。边际分析法是一种渐进的优化技术，用于分配短缺资源来获得最大效益。它可以被认为是通过对边际单元的效益和费用的权衡分析，以达到对有效资源的合理利用。边际分析法的思想就是在算法中每次只增加1个航材，看增加哪个航材所带来的费效比(即航材期望短缺量的减少与航材费用的比值［EBO(s－1)－EBO(s)］/c)最大，就将这个航材的数量增加1个。为证明边际分析法得出的解是最优解，需要证明 EBO(s)函数是凸函数。证明过程如下:

由于EBO(s)的一阶导数小于等于零，二阶导数大于等于零，根据凸函数定义可得EBO(s)是凸函数。

利用边际分析法求解分为两步:①针对单项的备件，在几个航站和基地之间优化配置库存量;②将所有种类的备件综合考虑，运用边际分析法优化配置库存量。具体的求解流程如图2所示。

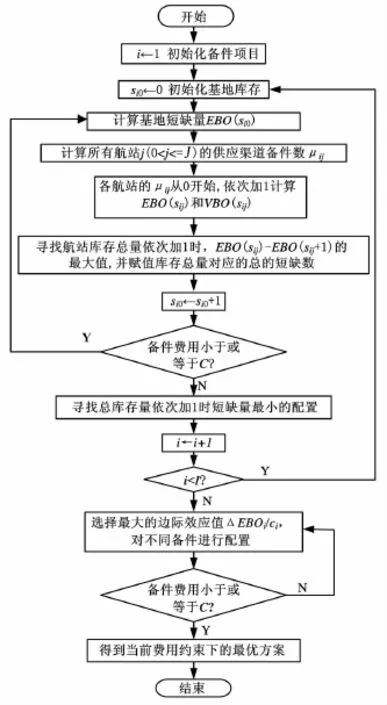
图2 多级库存模型求解优化流程

4 实例分析

以某航空公司购买的4架波音737－800推荐清单中的19项备件为例，航空公司的运营数据如下:N=4，TFH=3248.5h，T=40d，TRT=5d，假设两级维修保障组织的结构为一个基地，四个航站;备件对应参数如表2所示。

通过运用METRIC多级模型计算，可得19项备件的最优分配如表3所示(为节省篇幅，表3中未列出全部内容)。其中，N代表当前总的备件数量，Pi代表最新选择的备件，第3～7列代表当前选择的备件在各保障组织中的最优分配，第8～26列便是各备件对应的推荐数量。C代表当前总的成本，EBO是当前的总的短缺量。以第10行为例，当总的备件数由9增加到10时，此时应选择第19项备件，系统短缺量由3.68减少到3.53，总投入为43 259.82。备件19在基地与四个航站的分配量为2，0，0，0，0。其他18 项备件此时的数量为 (1，0，0，0，1，1，0，0，0，0，0，0，1，1，1，0，0，2)。

表2 备件参数表

根据最优分配表可以得到系统总的短缺量与成本间的最优曲线，如图3所示。

波音公司的19项备件对应的推荐数量为(1，1，1，1，1，1，1，1，1，1，1，1，1，1，2，2，2，3，3)，总资金是$1 328 080.18，而短缺量为0.611，如图2中的波音策略。将其与最优策略对比如下:

(1)相同短缺量对比。最优策略短缺量为0.533 时，所 需 资 金 为$917 462.32，节 约了 30.84%。

(2)相同资金对比。多级库存最优分配得出$1 269 647时，对应的19项备件推荐量为(6，2，1，2，6，6，2，1，1，2，2，6，6，6，7，1，1，8，7)，短缺量为 0.312，如图 2中的策略 1;剩余资金$58 433.26，不够支付最优曲线上的下一项备件16，但可以继续追加购买多项其他价低的备件，最终结果为(6，2，1，2，6，7，2，1，1，6，2，6，6，6，7，1，1，10，8)，此 时 的 短 缺 量 为 0.299，剩余$1424.3，如图2中的策略2。

表3 备件的最优分配表

图3 短缺量与成本优化曲线图

5 结语

由结果可知，多级模型在节约资金30.84%的前提下，仍能得到更优的短缺量;在资金相同时，通过多级模型优化后可得81项备件，远超过波音仅依据各种备件保障率计算得出的26项备件，充分体现了费效比最大的原则。价格低的备件多储备，如第5、6、18、19项备件;对于价格高、故障率相对低的备件尽量少储备，如16、17项备件。另外，通过最优分配表，可以直接得出各项备件在基地与航站的分配数量，既能指导航空公司在有限的采购资金的约束下进行新购机型的初始航材采购，达到最大的资金利用率，又可指导备件在各级保障站点的最优分配，体现了备件多级库存策略的有效性。此方案的有效性还有赖于进一步实践验证，或可采用仿真的方法对初始保障方案进行验证并优化。

［1］Sherbrooke C C.METRIC:Multi－echelon Technique for Recoverable Item Control［J］.Operations Research，1969，16(1):122-141.

［2］Graves S C.A Multi－echelon Inventory Model for a Repairable Item with One－for－one Replenishment［J］.Management Science，1985，31(10):1247-1256.

［3］Hillestad R J.Dyna－METRIC:Dynamic Multi－Echelon Technique for Recoverable Item Control［R］.US:Rand，1982.

［4］Axsater S.Modelling Emergency Lateral Transshipments in Inventory Systems［J］.Management Scientce，1990，36(11):1329-1338.

［5］Wong H.Stocking Decisions for Repairable Spare Parts Pooling in a Multi－line Base System［J］.Production Economics，2005，93(94):309-317.

［6］Kennedy W J，Patterson J W，Fredendall L D.An Overview of Recent Literature on Spare Parts Inventories［J］.InternationalJournalofProduction Economics，2002，76:201-215.

［7］王乃超，康锐.基于备件保障概率的多级库存优化模型［J］.航空学报，2009，30(6):1043-1047.Wang Naichao，Kang Rui.Optimization of Multi－echelon Repairable Item Inventory Systems with Fill Rate as Objective［J］.Acta Aeronautica et Astronautica Sinica，2009，30(6):1043-1047.

［8］孙江生，李苏剑，吕艳梅，等.武器贵重备件三级库存模型仿真研究［J］.兵工学报，2008，29(7):854-858.Sun Jiangsheng，Li Sujian，Lu Yanmei.Simulation and Research on the Three－Echelon Storage Model of the Valuable Spare Parts in Weapon Equipment［J］.Acta Armamentar，2008，29(7):854-858.

［9］王宁，司书宾，贾大鹏.服务水平约束下的多－单维修备件协同库存控制模型及其仿真研究［J］.中国机械工程，2007，18(23):2844-2847.Wang Ning，Si Shubin，Jia Dapeng.Multiple－single Inventory Cooperative Control Model and Simulation Research of Spare Parts under Restriction of Service Level［J］.China Mechanical Engineering，2007，18(23):2844-2847.

［10］杨华，郭伟，毕海玲，等.大型设备制造企业维修备件联合库存优化研究［J］.中国机械工程，2009，20(15):1802-1806.Yang Hua，Guo Wei，Bi Hailing，et al.Research on Pooling Inventory Optimization for Large Equipment Manufacturer’s Maintenance Parts［J］.China Mechanical Engineering，2009，20(15):1802-1806.

［11］倪现存，左洪福.基于边际效用的民机备件库存优化模型［J］.交通运输工程学报，2008，8(4):73-76.Ni Xiancun，Zuo Hongfu.Optimization Model of Spare Parts Inventory for Civil Aircraft Based on Marginal Utility［J］.Journal of Traffic and Transportation Engineering，2008，8(4):73-76.

［12］王乃超，肖波平，康锐.民机初始备件方案的优化［J］.北京航空航天大学学报，2010，36(9):1057-1061.Xiao Boping，Kang Rui，Wang Naichao.Optimal of Initial Spares Scenario in Civil Aviation［J］.Journal of Beijing University of Aeronautics and Astronautics，2010，36(9):1057-1061.