基于应力关系的岩石压缩系数变化分析

高书香

(承德石油高等专科学校石油工程系，河北承德 067000)

储层岩石的压缩系数对油气勘探、储量计算、油藏工程研究等都具有重要影响。常用的计算岩石压缩系数的Hall方法和Newmen方法仅考虑了岩石压缩系数随岩石孔隙度的变化［1］，但是岩石的压缩系数还受多个因素的影响［2－10］。另外，被测样品经过大量的处理过程，所受应力被多次改变，导致实验结果存在不可靠性。本文从油气生产过程分析入手，基于岩石压缩系数的定义式和岩石各应力间的关系式，经理论推导得出岩石三个压缩系数的理论表达式，并用他人的实验数据进行验证、分析与对比。

1 地下岩石的应力

岩石孔隙是由岩石骨架及孔隙中的流体共同支撑起来的空间。李培超［11］等在没有附加任何假设的前提下，得出了描述孔隙空间大小、骨架应力、孔隙压力之间关系的方程式:

式中σ为岩石上覆应力，σs为岩石骨架应力，p为孔隙压力，φ为孔隙度。

当孔隙压力p变化后，首先引起的是岩石的骨架应力发生变化;而骨架应力的变化会引起岩石骨架的伸缩或变形，从而导致孔隙体积的变化。因此，可以用单位孔隙压力变化引起的骨架应力变化量的大小来描述岩石在孔隙压力变化情况下的孔隙度、压缩系数等的变化规律。设:

则λ为岩石的骨架应力随孔隙压力的变化量，其大小与与岩石骨架及孔隙压力变化量有关。本文中为方便而称λ为骨架应力变化系数。从上述分析可以看出，λ的大小直接影响岩石的孔隙体积、骨架体积、骨架应力、孔隙度、压缩系数等参数值，但却受岩石骨架成分、骨架强度、骨架结构等多种因素的影响。

2 压缩系数关系式

2.1 三个压缩系数及其关系

根据文献［12］中的定义，岩石孔隙体积压缩系数Cp、骨架体积压缩系数Cs、整体体积压缩系数Cb分别为:

则通过化简、变形，可得下列关系式:

设Css为单位骨架应力变化导致的岩石骨架体积的变化率，本文中称为骨架参数(为使Css为永正，在式中加负号)。则有:

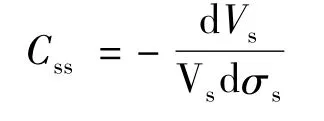
因此，岩石的Css是岩石骨架的固有参数。岩石的骨架体积压缩系数Cs可表示为λ和Css的函数:

2.2 孔隙度随孔隙压力的变化

假设岩石的上覆应力σ不变，对(1)式两端求全微分并变形得:

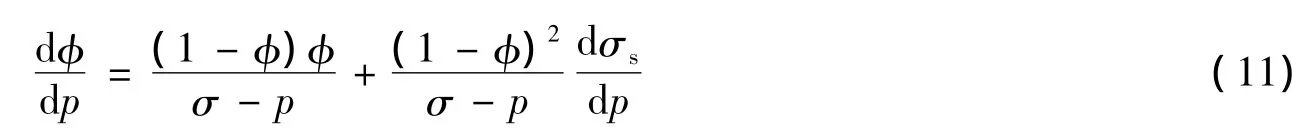
将(2)式代入，则变形为:

石油生产过程中，导致岩石孔隙度φ变化的根本原因是孔隙压力p变化，但直接原因却是骨架应力σs变化。将方程式(11)绘制在以λ为横坐标、以dφ/dp为纵坐标的坐标系中，得到如图1所示的一条单调递增的直线。根据方程式(11)或图1，可定性判断当孔隙压力p降低后，孔隙度φ和骨架应力σs随之变化的趋势，如表1所示。由于孔隙度φ随孔隙压力p的降低而降低，故λ的理论取值范围为［－φ/(1－φ)，∞)。

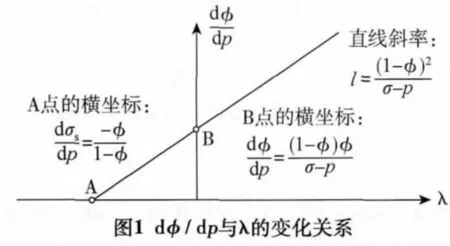
表1 孔隙压力降低后骨架应力和孔隙度的变化

2.3 压缩系数随孔隙度和孔隙压力的变化

将式(12)分别代入式(8)和式(9)得:

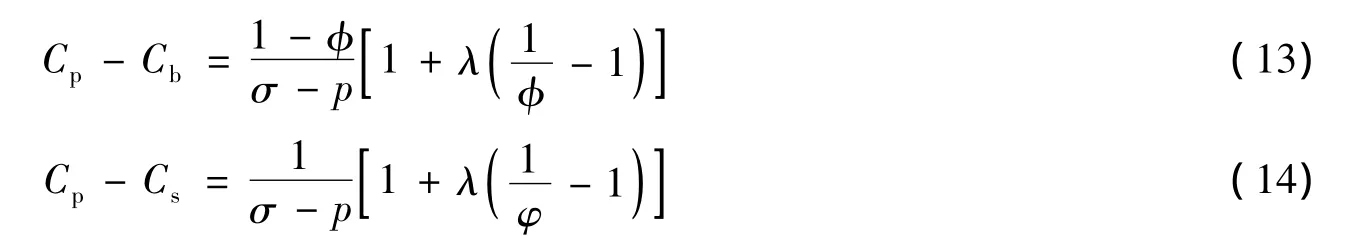
将式(10)代入式(14)得:

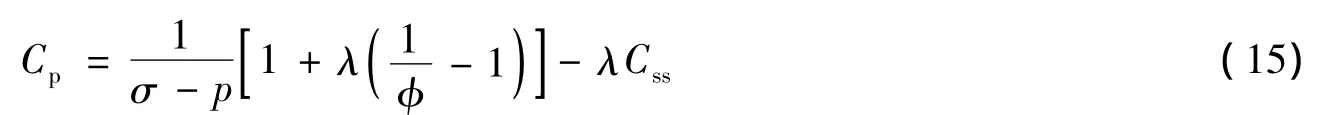
将式(15)代入式(13)得:

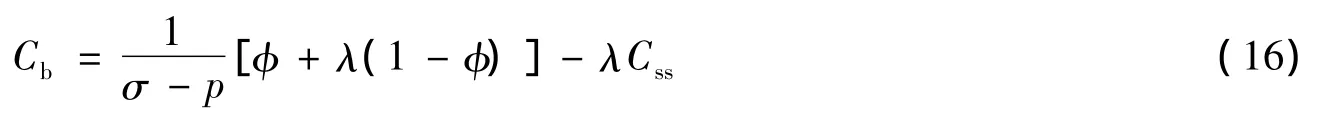
从式(10)、(15)、(16)可以看出，三个压缩系数都可以表示为σ、φ、p、λ和Css五个参变量的函数。对于某特定地层中的岩石，上述五个变量的值都是确定的，因此，地层岩石的三个压缩系数都有唯一确定的值。

式(15)和式(16)分别对φ求偏导得:

因此，当λ在不同的范围内取值时，孔隙度φ对孔隙体积压缩系数Cp和整体体积压缩系数Cb的影响也不同。

根据式(10)，岩石的骨架体积压缩系数只与λ和Css两个参数有关，与孔隙度φ无直接关系。当λ＜0时，骨架体积压缩系数Cs为正，骨架体积随孔隙压力的降低而减小;当λ＞0时，骨架体积压缩系数Cs为负，骨架体积随孔隙压力的降低而增加;当λ=0时，骨架体积压缩系数Cs为0，即孔隙压力变化过程中骨架体积不变。

设peff=σ－p，则peff即为岩石的有效上覆应力。根据式和式，其它参数不变时，岩石的孔隙体积压缩系数Cp和整体体积压缩系数Cb均随有效上覆应力的增大而减小。因此，其它参数不变时，孔隙压力越低，Cp和Cb越小;地层压力系数越大，Cp和Cb越大;岩石埋藏越浅，Cp和Cb越大。

2.4 Cs对Cp大小的影响

根据式(15)，假设:

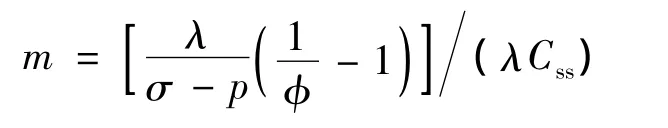
化简得，

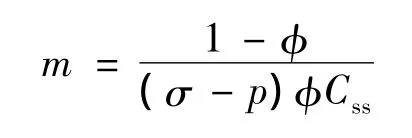
则当 φ、peff、Css同时取高值时，m 值较小。假若 φ =50%，peff=100 MPa，Css=1 ×10－3MPa－1，则 m=10;若φ=40%，peff=100 MPa，Css=1×10－4MPa－1，则m=150。因此，岩石的骨架体积压缩系数Cs远小于孔隙体积压缩系数Cp。故在室内实验测定中，完全可以忽略Cs。

当忽略Cs时，式(9)和(14)可分别改写为:

3 变化与分析

根据文献［7］中测定的不同净有效上覆应力增量下的孔隙体积Vp值，通过转换横坐标，可以得到不同孔隙压力下的孔隙体积Vp，如图2所示;然后进行二阶多项式曲线拟合后即可得到形如下式的关系式:

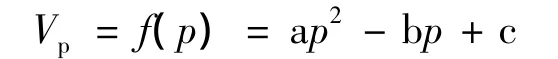
式中，a、b、c为拟合常数，p为孔隙压力。这样可利用下式求其孔隙体积压缩系数Cp:

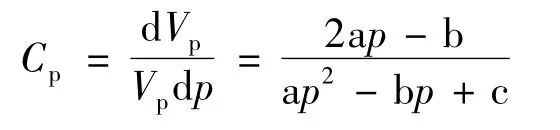
计算结果如表2和图3所示。结果显示，相同有效上覆应力条件下，不同岩石的孔隙体积压缩系数Cp随孔隙度φ的增加而降低。

根据方程式(20)，利用Cp、φ、peff可反算λ的大小，如表3所示。结果显示，所有岩石的λ值均小于0，且多是接近于λ边界值。图4是文献［7］中岩心1-93/106的实验数据拟合值和用本文关系式计算值的对比。

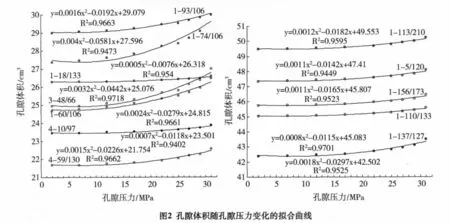
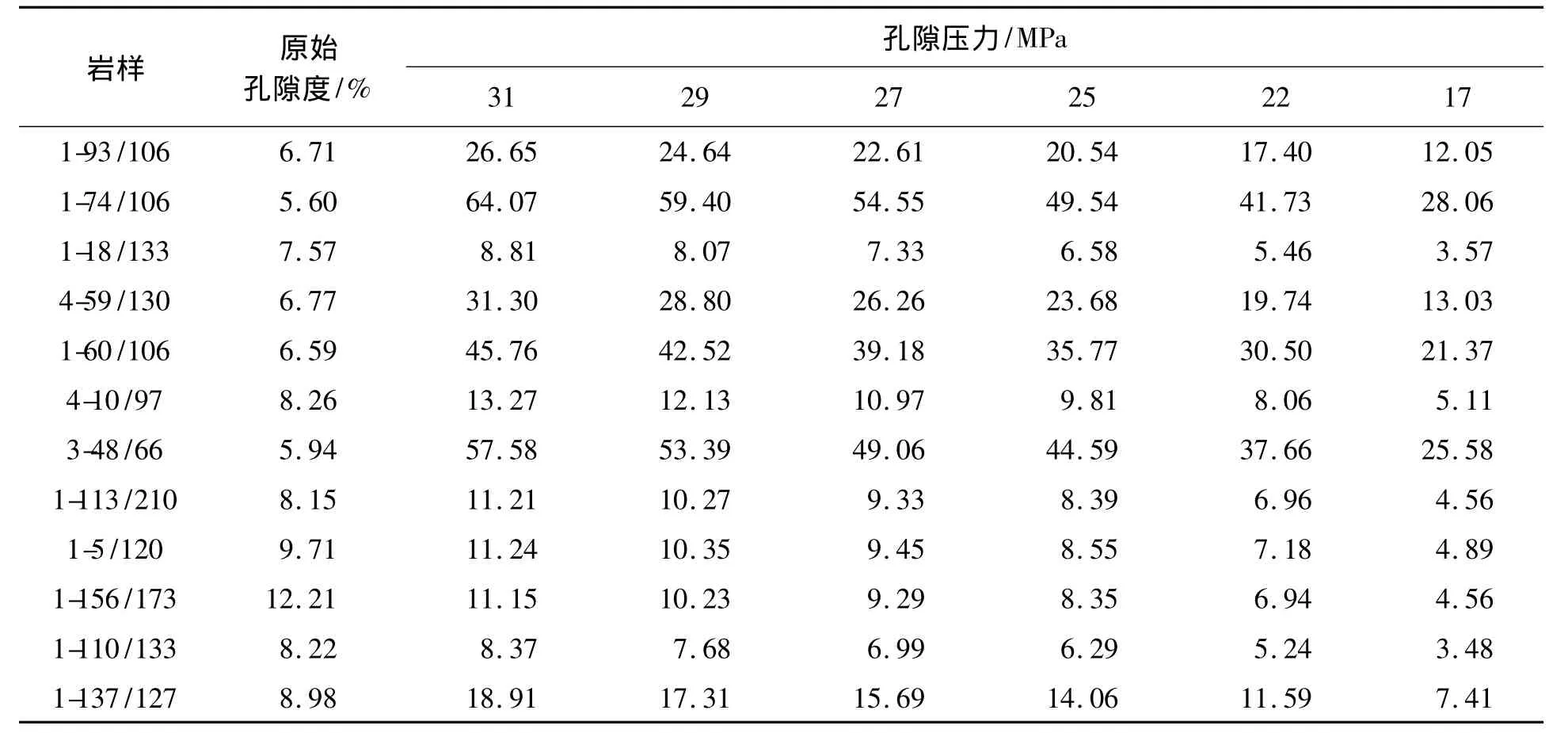
表2 不同孔隙压力下各岩样的孔隙体积压缩系数

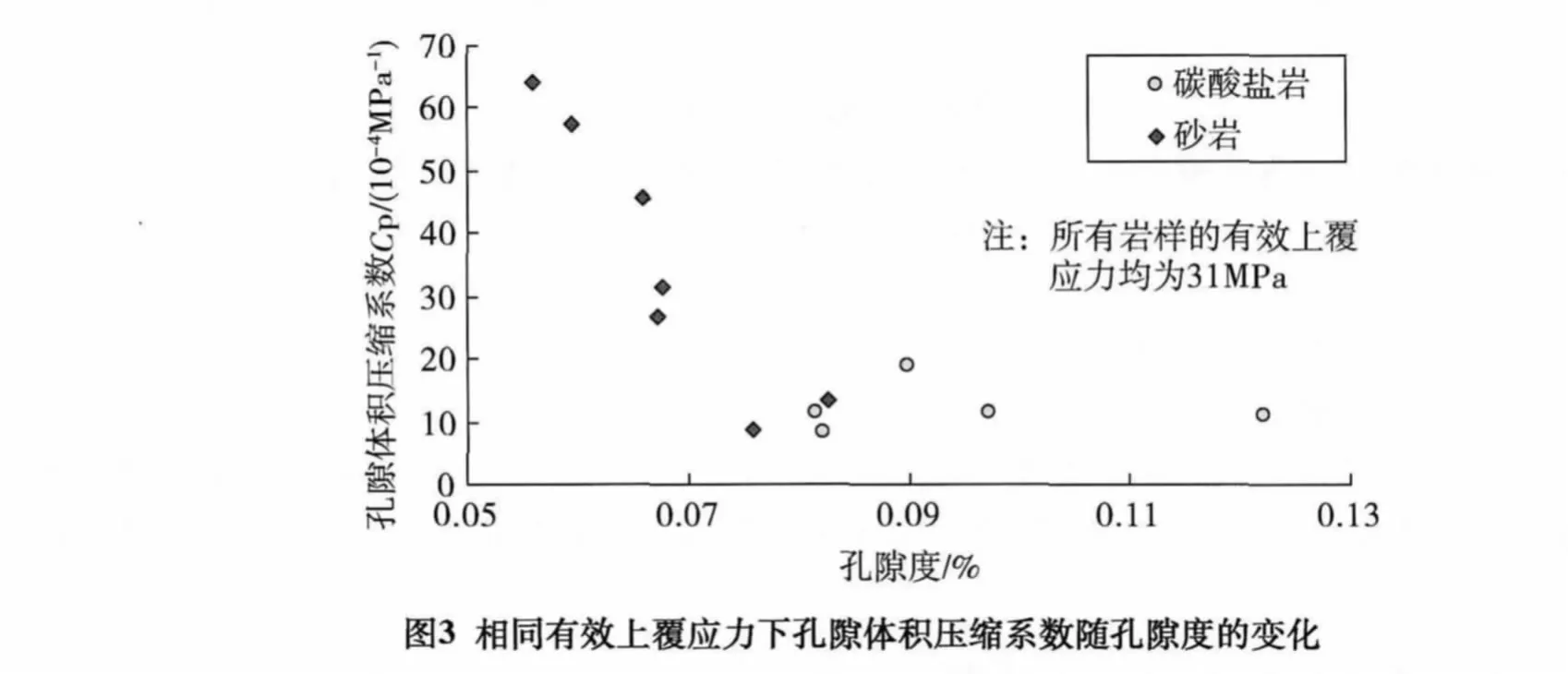
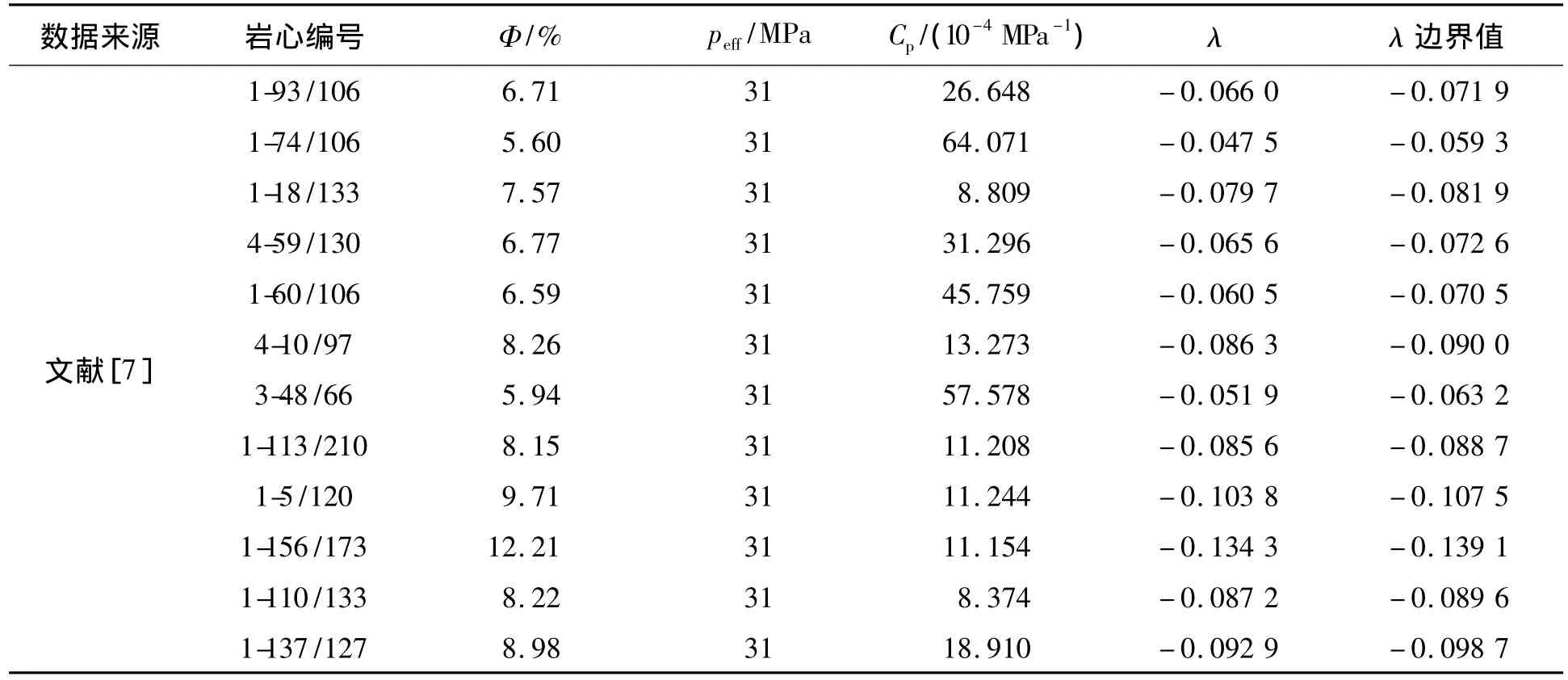
表3 根据实验结果计算的λ值

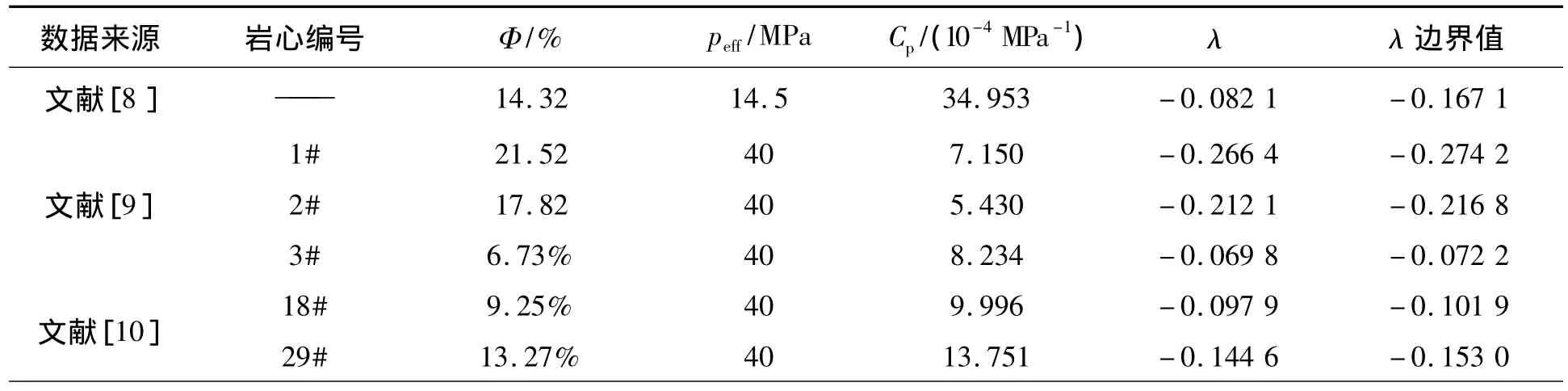
续表

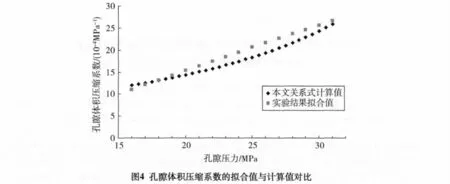
4 结论

1)定义了岩石的骨架应力变化系数λ，其大小与岩石骨架及孔隙压力变化量有关，岩石骨架的成分、强度、结构等会影响λ的大小。

2)岩石的孔隙体积、骨架体积、骨架应力、孔隙度、压缩系数(Cp、Cs、Cb)等均受骨架应力变化系数λ的影响。

3)随孔隙压力降低，岩石的孔隙度降低。

4)岩石的骨架体积压缩系数可表示为λ和Css的函数。

5)数据证明岩石的骨架体积压缩系数Cs远小于孔隙体积压缩系数Cp，在室内实验测定中，可完全可以忽略Cs。

6)相同有效上覆应力条件下，不同岩石的孔隙体积压缩系数Cp随孔隙度φ的增加而降低。

7)岩石的骨架应力变化系数λ的取值范围不同，σs、φ、Cp、Cs、Cb的变化趋势也会不同。

［1］杨东东，戴卫华，张迎春，等.渤海砂岩油田岩石压缩系数经验公式研究［J］.中国海上油气，2010(5):317－319.

［2］王卫红，郭艳东，刘华.超高压气藏单井控制动态储量评价方法［J］.新疆石油地质，2011(3):291－294.

［3］樊怀才，李晓平，陈军，等.计算异常高压气藏地层压缩系数的一种新方法［J］.西安石油大学学报(自然科学版)，2012(2):41－45.

［4］魏俊之，郑荣臣.异常高压气藏储集层的岩石压缩系数和边底水规模对开采特征的影响［J］.石油勘探与开发，2002(5):56－58.

［5］朱玉新，谢兴礼，罗凯，等.克拉2异常高压气田开采特征影响因素分析［J］.石油勘探与开发，2001(5):60－63.

［6］刘琦，卢耀如，李晓昭.孔隙水压力对岩石力学参数的影响［J］.地球学报，2008(10):660－664.

［7］高博禹，周涌沂，彭仕宓.储层孔隙度应力敏感性研究［J］.石油实验地质，2005(2):197－202.

［8］张新红，秦积舜.低渗岩心物性参数与应力关系的试验研究［J］.石油大学学报(自然科学版)，2001(4):56－60.

［9］汪周华，郭平，周道勇，等.注采过程中岩石压缩系数、孔隙度及渗透率的变化规律［J］.新疆石油地质，2006(2):191－193.

［10］李莲明，李治平，车艳.一种定量研究非线弹性岩石体积应变新方法［J］.天然气地球科学，2011(1):129－135.

［11］李培超，孔祥言，李传亮，等.地下各种压力之间关系式的修正［J］.岩石力学与工程学报，2002(28):3899－3902.

［12］陈元千，邹存友.三种岩石压缩系数关系的推导与对比［J］.新疆石油地质，2012(4):459－460.