面向工程应用的数值积分法仿真实验
2013-12-04李杰
李 杰
(承德石油高等专科学校热能工程系,河北承德 067000)
数值积分法[1]发展到今天,已有许多种拟合手段,迄今为止,应用最广泛的当属四阶龙格-库塔法[2],并以变步长的龙格库塔法为优。但鉴于其计算量和计算精度有待进一步提高,有必要进一步寻找出最佳步长,以便在不无限地减小步长条件下达到较高的精度,从而得出一个较可靠的步长值,供分析实际工程系统的稳定性作参考使用,对此本文做了大量的实验数据及实验图像,进而分析得出了最佳仿真时间与仿真步长[2]。
1 实验原理及仿真步骤
1.1 实验原理
运用matlab[3]中的命令语句ctrb(a,b)与obsv(a,c),分别对其用命令语句rank取秩,以此判断其可控性与可观察性。
1.2 仿真步骤
编制RK-4仿真程序,绘制出单输入单输出及多输入多输出曲线图[4]。仿真程序流程如图1所示:
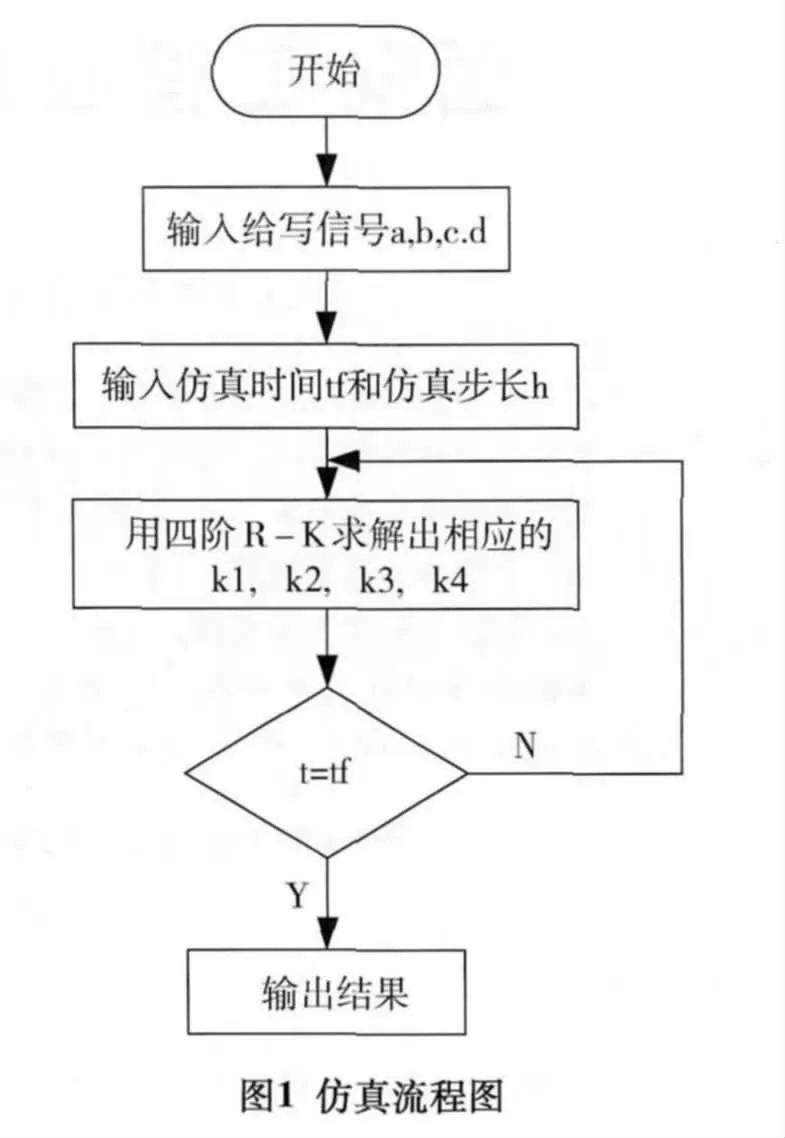
1.3 软件程序代码
仿真用原程序代码清单如下:


2 实验仿真结果
在实验中,选取了大量不同的仿真时间tf以及步长h,从中挑选出如下几种最具代表性的实验图像(图2—图11)。
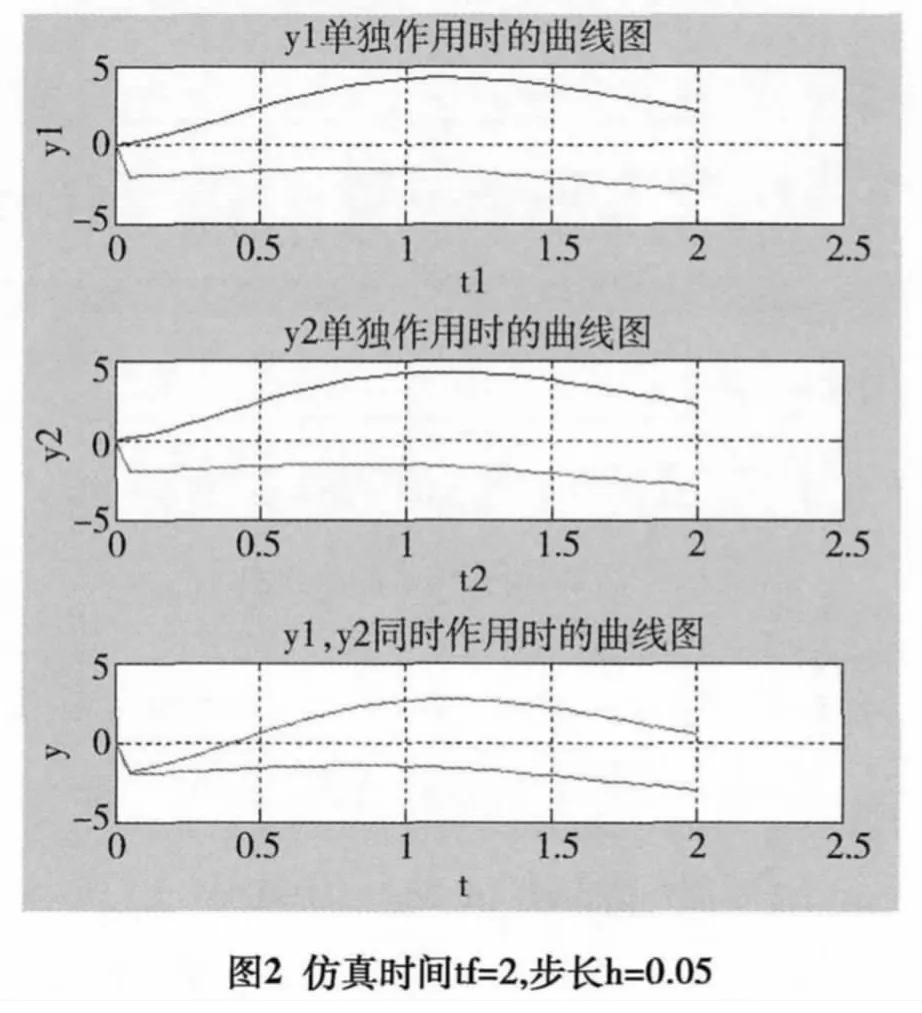
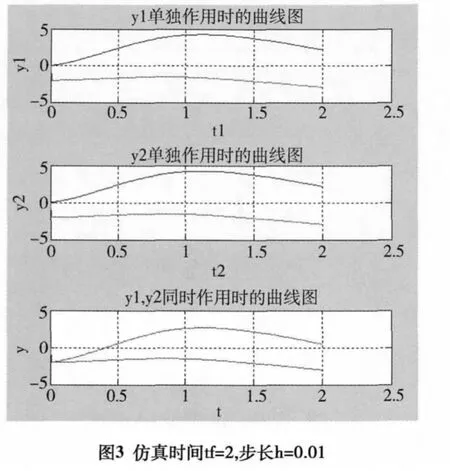
由图2、图3可以看出当仿真时间tf=2,仿真步长分别为:h=0.05,h=0.01时,波形明显变缓,过渡过程时间明显加长,系统达到稳定时所用时间过长,严重影响控制系统的实时性。
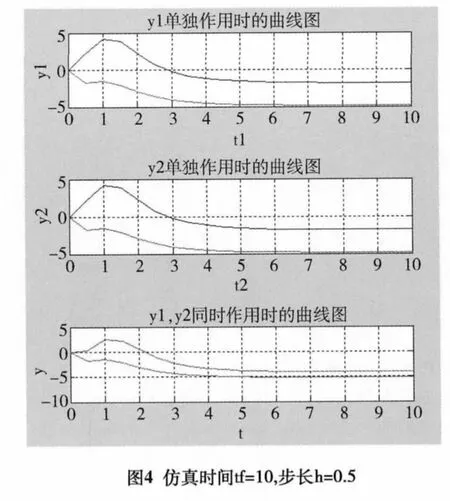
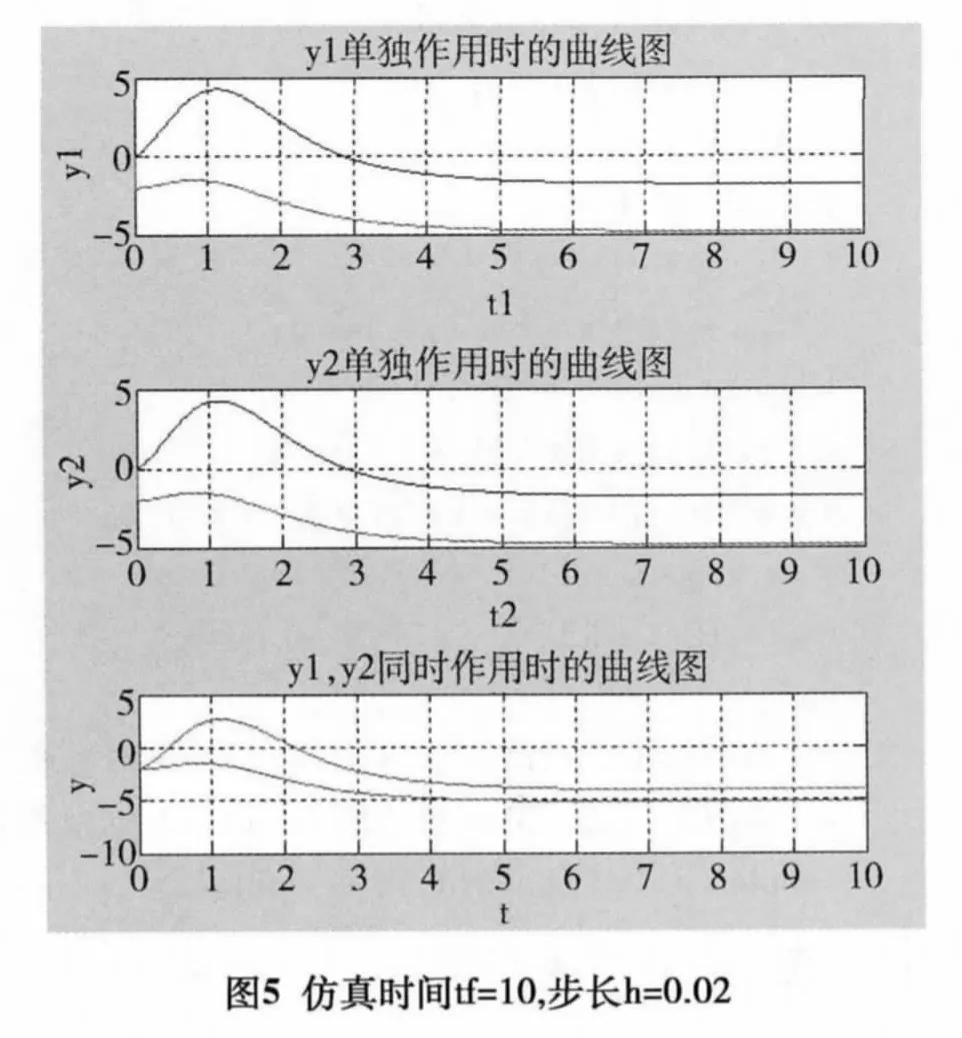
由图4可以看出当仿真时间tf=10,仿真步长h=0.5时,波形开始变陡,过渡过程时间缩短,但波形明显失真,不利于控制系统的稳定性。由图5可以看出,随着仿真步长的减小,当h=0.02时,波形明显无失真。
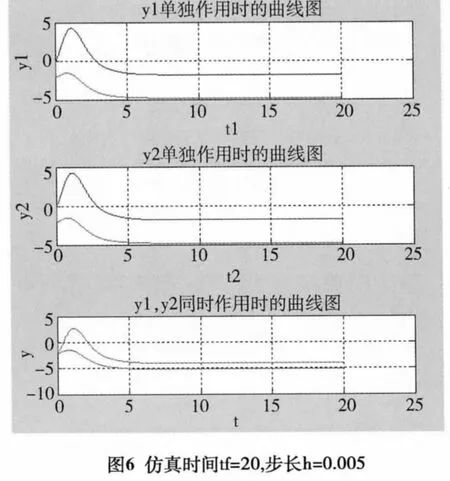
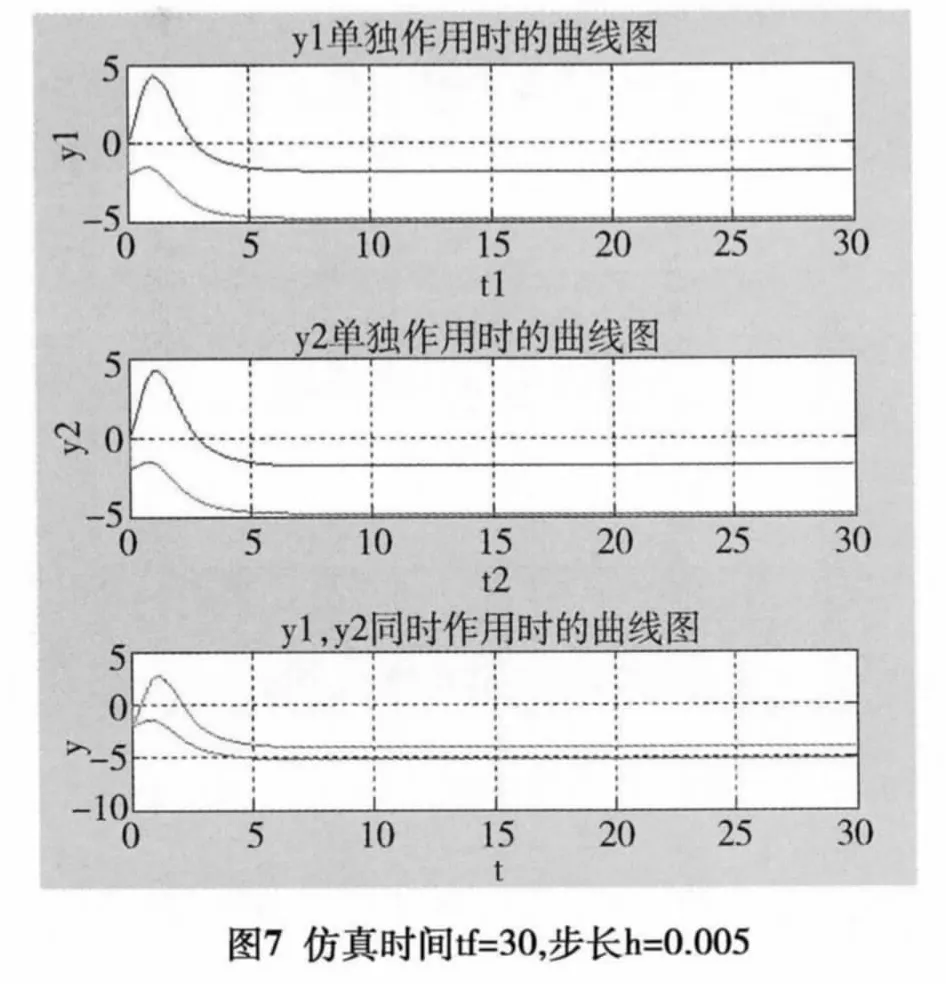
由图6可以看出当仿真时间tf=20,仿真步长h=0.005时,波形开始变缓,过渡过程时间明显缩短,波形明显变好,有利于控制系统的稳定性,并可提高系统的实时性。由图7可以看出,随着仿真步长的增大,tf=30,步长h=0.005时,波形进一步变陡,可缩短系统达到稳态时所用时间,但不利于控制系统的稳定性。
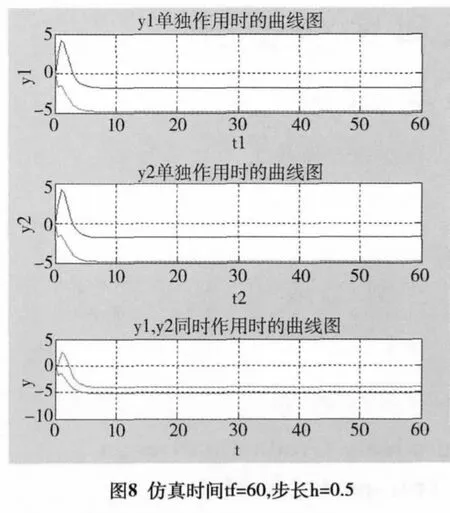
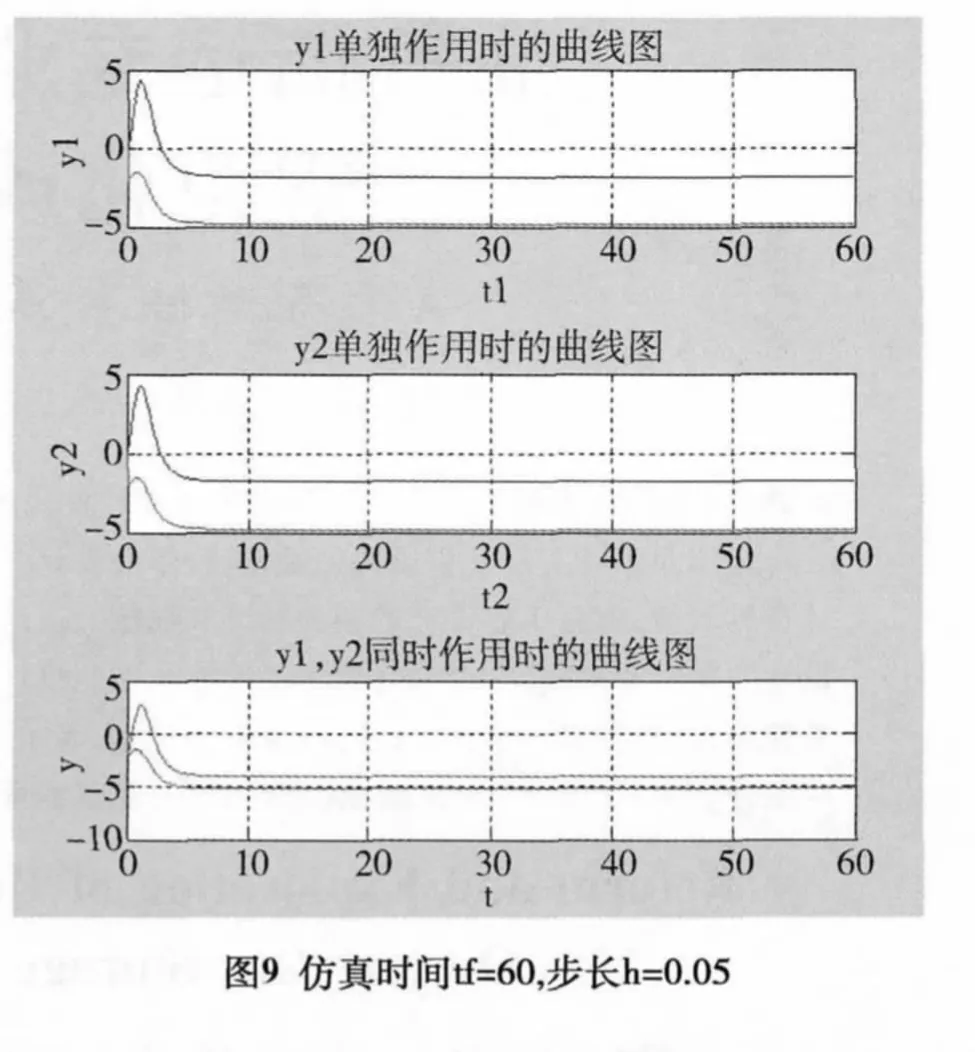
由图8可以看出当仿真时间tf=60,仿真步长h=0.5时,仿真速度明显提高,过渡过程时间明显缩短,但波形明显变陡,部分图形失真,仿真精度降低,不利于控制系统的稳定性。由图9可以看出,随着仿真步长的减小,步长h=0.05时,波形无失真,虽然可提高仿真的精度,但波形明显变陡,同样不利于控制系统的稳定性。
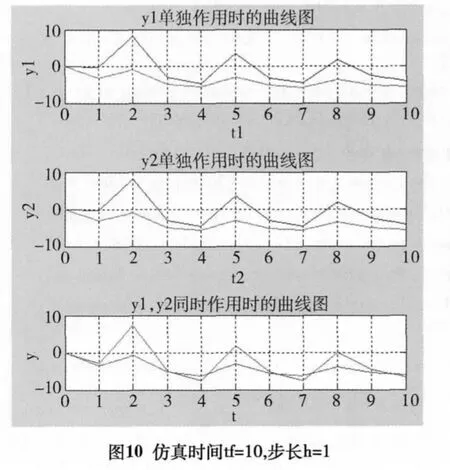
由图10,图11明显看出,随着仿真步长的增大,当仿真步长h=1时,不论仿真时间增大还是减小,波形严重失真,控制系统变的不稳定性,难以控制,更谈不上仿真的速度与精度。
3 结论

本文通过大量的仿真图形与数据分析得出结论:当仿真时间tf大于20秒时波形明显变陡,但当仿真时间tf小于20秒时波形明显变缓,但过渡过程时间明显加长,综合分析最佳仿真时间为tf=20,当步长为h等于0.2时波形开始失真,等于1时算法不稳定,当等于0.001时运行时间明显加长,当步长等于0.005时为最佳步长,同时把本实验得出的结果应用于实际工程,结果较为理想。所以得出:最佳仿真时间tf=20,最佳仿真步长h=0.005,当h=0.2时波形开始失真h=1算法不稳定。
[1]刘廷建.数值计算方法[M].成都:成都科技大学出版社,1997.
[2]沈艳霞,周平.MATLAB在电力电子学仿真中的应用[J].无锡轻工大学学报,2001,20(1):92~94.
[3]刘卫国,陈昭平,张颖.MATLAB程序设计与应用[M].北京:高等教育出版社,2002.
[4]邓国扬,盛义发.基于Matlab Simulink的电力电子系统的建模与仿真[J].南华大学学报(理工版),2003,17(1):1~6.
