时间序列模型在医院感染发生率拟合预测中的比较研究*

李 红 潘东峰 郭忠琴 王 岚 梁沛枫△

随着现代医学的快速发展，侵入性诊疗技术的开展以及放、化疗等使医院感染发生的影响因素复杂化，医院感染不断出现新的特点，产生新的危害，其已成为医学界亟待解决的重大问题。医院感染的监测能及时发现医院感染病例及其相关因素，可有效降低其发生率。目前对医院感染的监测虽已从全面综合性监测转向针对性强的目标性监测或靶位监测，但感染控制的监测模式仍处于“形式化”感控阶段〔1〕，实现对医院感染危险因素造成的危害进行事前监测，从而建立医院感染预警模式则是医院感染管理工作今后发展的重要方向。利用统计预测分析技术，对医院感染进行预测性数据挖掘是对医院感染危险度监测的前瞻性研究方法。本研究选择宁夏某大型综合医院为监测点，尝试应用三种不同的时间序列模型对医院感染发生率进行模拟构建，探讨模型在医院感染领域应用的适用性及价值，并应用最优时间序列模型以间接监测医院感染发展趋势，以期发现医院感染的潜在规律，发出早期预警，从而提高监控效率。

资料与方法

1．资料来源

资料来源于宁夏某三甲医院2005年1月1日至2011年10月31日出院病人数据库及该院医院感染监测网。

2．数据整理

将医院HIS系统中的2005～2010年出院病人数据库转换为能满足统计预测分析所需的数据环境，并筛选符合医院感染诊断标准的全部病例，对筛查出的医院感染病例与医院感染监测网上报的院感病例进行核对，补全数据库中漏填病例，计算医院感染发病率。诊断标准及感染率计算方法根据卫生部颁布的《医院感染诊断标准(试行)》。

3．方法简介

(1)ARIMA 模型〔2－3〕，即自回归滑动平均混合模型，主要分析时间序列的随机性、平稳性和季节性。ARIMA模型中的三个参数p、d、q分别表示自回归阶数、差分阶数和移动平均阶数，其数学表达式为:

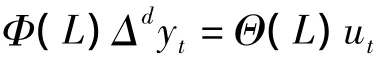
其中Φ(L)和Θ(L)分别表示L的p，q阶特征多项式;t表示时间;yt表示时间序列;ut为白噪声过程。若序列具有线性趋势或周期性，可通过d阶差分或季节差分使序列满足ARIMA的建模条件，最后通过残差序列检验拟合的模型是否有效，并可通过AIC准则或BIC准则判断多个模型中的最优模型。

(2)指数平滑法〔2〕的原理是对离预测期较近的观察值赋予较大的权数，对离预测值较远的观察值赋予较小的权数，权数由近到远按指数规律递减。其基本形式的数学表达式为:

其中，yt是实际值序列，是平滑值序列，是上期平滑值，α是平滑系数，也叫衰减因子，平滑系数的取值范围为:0≤α≤1。

(3)灰色模型〔4－5〕的理论基础是一般的非负准光滑序列经过累加生成后，都会减少随机性，呈现出近似的指数增长规律。原始序列越光滑，生成后指数规律与越明显。其数学表达式为:

其中，z(1)k=1/2［(x(1)(k)+x(1)(k－1)］GM(1，1)模型中的参数－a为发展系数，b为灰色作用量。－a反映了及的发展态势。

(4)模型效果的评价

采用相对误差绝对值平均MAPE(mean absolute percentage error)及其相应的等级评定〔5〕来评价ARI-MA模型、指数平滑模型、灰色模型对医院感染发生率资料的拟合效果。

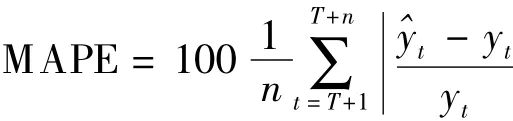
T表示样本容量，n表示样本外预测期数，^yt表示预测值，yt是实际值。

4．分析软件

ARIMA模型和指数平滑模型运用eviews6．0进行拟合，灰色模型应用《灰色系统理论及其应用》〔4〕一书的配套软件进行建模。

结 果

1．医院感染时序图

以医院感染的月发病率信息为纵轴，对应的时间为横轴，绘制医院感染率时序图(图1)，时序图显示各月医院感染的发病率呈现出一定波动，且每年均出现发病高峰月，医院感染率具有季节性和周期性。

图1 宁夏某三甲医院医院感染率时序图

2．ARIMA 模型

对医院感染率序列进行季节调整后的单位根检验再次确定了医院感染的季节性，对原变量进行一阶差分、季节差分后，尝试拟合不同的ARIMA季节模型，依据信息量准则判别模型的优劣，其中AIC和SBC最低的模型是最好的模型。最终确定模型为ARIMA(0，1，1)(0，1，1)12，其 AIC 和 BIC 值分别为 1.9047、1.9752。通过残差自相关函数图检验模型的随机误差项是一个白噪声序列。故 ARIMA(0，1，1)(0，1，1)12模型是所要确定的最终模型，其对应的模型表达式为:

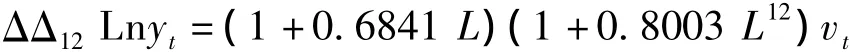
医院感染序列实际值与预测值的MAPE值为12.50，对应的拟合图形如图2。

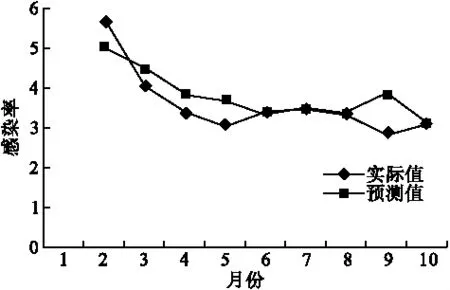
图2 感染率实际值与ARIMA模型预测值趋势图

3．指数平滑模型

对原序列拟合加法性季节Holt-Winters法和乘法性季节Holt-Winters方法，其残差平方和分别为19.34和19.38，以残差平方和最小为最合适模型，并进行残差图检验，最终加法性季节Holt-Winters法是指数平滑法中最合适模型。其对应的模型表达式为:

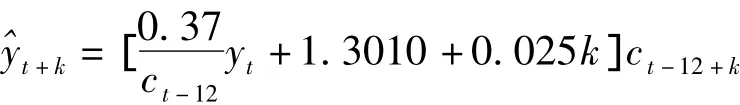
医院感染序列实际值与预测值的MAPE值为10.41，对应的拟合图形如图3。

图3 医院感染率实际值与指数平滑法预测值趋势图

4．灰色模型

对原序列进行灰色模型的可行性判断，结果显示，σ(k)∈(0.5000，2.6242)，级比检验满足建模的基本要求，由于原序列具有季节性及渐升趋势，故采用灰色季节趋势法对模型进行拟合。最终模型通过后验检验，对应的模型表达式为

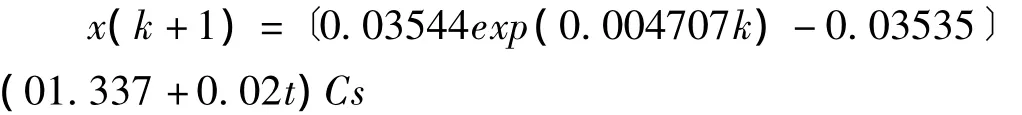
医院感染序列实际值与预测值的MAPE值为19.03，对应的拟合图形如图4。

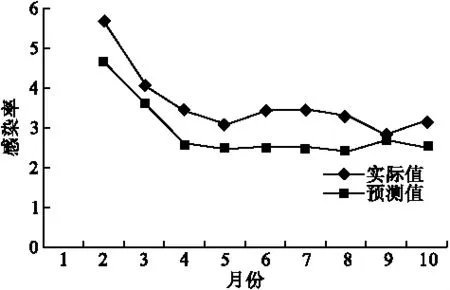
图4 医院感染率实际值与灰色模型预测值趋势图

5．模型评估

以2011年1～10月的医院感染发生率资料作为模型评价样本，对上述三种时间序列模型应用MAPE值判断其预测精度，结果见表1。

三种时间序列模型的预测精度均为良好，其中指数平滑模型预测值与实际值间的MAPE值最小，为10.41，故指数平滑模型为该医院感染发生率预测模型的最优模型。

表1 不同月份各时间序列模型预测MAPE值及等级评价

讨 论

统计预测是在大量统计资料的基础上，运用数理统计方法研究事物发展变化趋势和方向的预测方法。常用统计预测方法很多，诸如回归分析法、时间序列法、灰色模型等等。有研究显示，各种模型在疾病的预测中及医院管理等方面均取得了较好的效果〔6－8〕。在国内外研究中，灰色模型、季节性时间序列的线性模型、人工神经网络模型均已应用于医院感染危险度的预测中，取得了良好的预期效果〔9－11〕。但医院感染的发生受多种因素共同作用影响，在特定环境中，医院感染发生率及其发展变化的趋势不尽相同，在对特定医院的医院感染进行监控时，为提高监控效率，可应用统计预测技术进行院感的前瞻性研究，但哪种模型更适合该医院的医院感染危险度的预测，还需进一步探索。本文应用ARIMA模型、指数平滑模型、灰色模型对特定的医院感染危险度进行构建，取得了预期效果，拟合值和实际值间预测的相对误差绝对值平均在10～20之间，预测精度为良好，说明这三种对医院感染率的预测具有可行性，其对医院感染率的发生趋势判断具有参考价值。

ARIMA模型、指数平滑模型、灰色模型除其基本形式外，又都包括了多种衍生类型，各类型都有其不同适用条件，在模型拟合时一定要根据原序列的特征确定不同的模型类型才能得到较好的预测效果。本例资料由于有明确的季节性，故在各模型拟合时均选择季节性类型。从三种模型拟合的趋势图看，灰色模型的预测值普遍小于其实际值，而ARIMA模型和指数平滑模型的预测值的拟合图形轨迹与实际值较吻合，特别是指数平滑模型，其可能是由于ARIMA模型在操作过程中考虑到了序列的随机性、平稳性和季节性，而指数平滑模型在考虑了整体均值、整体趋势和季节性的同时又考虑的序列的最邻近的值。医院感染的发生虽有其明显的季节性，但随机性也较强，ARIMA模型和指数平滑模型都考虑了其随机性，而灰色模型只能用于数据离散较小且发展趋势呈单调性的情况，无法分析系统的波动规律〔12〕，即使在事先对数据进行了预处理，剔除了其趋势性和季节性，但对序列随机性的把握仍欠缺，且灰色模型在拟合时，由于其软件只包含基本形式的预测用程序组，对其趋势性和季节性均需先运算剔除后再回代，整个操作过程较前两种模型复杂。

由于医院感染的发生率资料收集相对较方便，故本次研究仅对医院感染的发病率建立了一维的时间序列模型，在研究中发现其具有较强的可操作性和现实意义。但医院感染的发生是诸多因素综合影响的结果，可尝试利用多元统计分析方法，将各影响因素的作用融入模型，借助先进工具进行分析预测，可能会使结果更加贴近实际，更具操作性。

1．王良俊，周霞，杨金霞，等．医院感染监测中存在问题及对策．中华医院感染学杂志，2008，18(4):492-493．

2．孙振球．医学统计学．第2版 北京:人民卫生出版社，2005，7:461-462．

3．王燕．应用时间序列分析．第2版，北京:中国人民大学出版社，2008，12:149-150．

4．刘思峰，谢乃明，等．灰色系统理论及其应用．北京:科学出版社，2008．

5．刘思峰．预测方法与技术．北京:高等教育出版社，2005．

6．尹志英，缪明正．指数曲线模型在预测甲肝流行趋势中的应用．中国卫生统计，2007，24(5):555．

8．胡兴，胡锡健．新疆H1N1甲型流感预测模型的比较研究．中国卫生统计，2011，28(3):342-343．

7．肖玉霞，张颖．用线性趋势季节模型预测出院人次．中国卫生统计，2008，25(3):213-215．

8．罗阳，丁国英，府伟灵，等．季节性时间序列分析在医院感染中的应用．中华医院感染学杂志，2005，15(4):390-392．

9．张素萍，王建斌，吴俊霞，等．医院感染灰色模型监控效果的探讨．中华医院感染学杂志，2000，10(5):380-381．

11．许林勇，白毅，胡明，等．基于人工神经网络模型的医院感染危险度预测．中南大学学报，2006，31(3):404-407．

12．颜杰，相丽驰，方积乾．灰色预测模型及SAS实现．中国卫生统计，2006，23(1):75．