基于赫兹理论的计算机直接制版设备辊筒模态分析*

2013-12-03胡志炜孙海达汪佳敏

机械研究与应用 2013年6期

胡志炜，孙海达，汪佳敏

(柯达电子(上海)有限公司，上海 201206)

1 引言

计算机直接制版设备[1]CTP(Computer To Plate)的主要运动是辊筒和丝杠的旋转。在制版过程中，由于刻版的需求，辊筒旋转的速度远远超过丝杠旋转的速度。CTP曝光的时间由辊筒的转速决定。提高辊筒的转速意味着出版速度的提高，效益的提升。CTP作为印前设备，辊筒上轻微的振动都会影响设备的动态性能导致后续印刷时出现网点扩大、重影、线条抖动、墨色不均等质量问题。尽管在辊筒设计、制造与安装上进行了众多的考虑，还有很多理论的问题需要解决，很有必要分析其动态性能。推导赫兹接触非线性理论并利用Ansysworkbench来对辊筒进行模态分析，研究其振动特性，为后续提高辊筒的旋转速度提供理论依据。

2 赫兹接触理论[2]

CTP设备的辊筒两端采用的是瑞典SKF的深沟球轴承6208ZZ，滚动体和内外圈在不受力的情况下，其接触为点接触。在受到外力的作用下，点接触发生变化过渡至面接触，处于小变形状态，同时滚动体和内外圈之间比较光滑，摩擦力远小于受到的外力，可忽略不计，又因为接触区域长度远小于滚动体和内外圈的半径，所以深沟球轴承中的滚动体和内外圈符合赫兹点接触理论。

滚动体和内外圈的接触的几何条件如图1所示，两弹性体相交于空间坐标系O点，并以过点O与滚动体和内外圈的公切平面为x1y1平面，指向滚动体和内外圈内部的坐标轴为z1z12。图中P1、P2为接触区域点x1、x2处的作用力。

图1 滚动体和内圈接触

根据余弦定理可以认为接触区域点O附近沿Z轴的位移为:

(1)

设点O附近对应x1和y1的滚动体和内外圈表面上对应点为P1和P2，由式(1)可知，其对应x1和y1载荷作用前沿Z轴方向的距离为：

(2)

利用坐标变换，将x1y1乘积项的系数变为0，得到：

z1+z2=A0x2+B0y2

(3)

载荷作用后，点P1和P2沿着Z轴方向的位移为ω1和ω2，由图1可知：

ω1+ω2=δ-(z1+z2)

=δ-A0x2-B0y2

(4)

式中：δ是两接触体的弹性趋近量[3-4]。

根据法向集中力P作用在弹性半空间表面(x′,y′)点，另外一点(x,y)将有法向位移的Boussinesq解：

(5)

式中：E、V是滚动体和内外圈的弹性模量和泊松比。

若p为半空间表面局部区域S上的分布压力p(x′,y′)时，接触区域任意(x,y)点的法向位移由Boussinesq解均可表示为:

(6)

若接触区域S为椭圆，则有:

(7)

压力p按照半椭球函数进行分布，如图2所示，可得出：

(8)

式中:a,b分别为椭圆区域S的半长轴与半短轴；P0是椭圆中心处的压应力。

由式(6)可得分布压力p(x′,y′)在(x,y)处产生的沿Z轴的法向位移：

(9)

为了积分方便将dx′y′ 表示为r′dr′dθ′，弦长C′D′长度以2l′来表示，如图3所示。

图2 接触应力分布图3 椭圆区域S的xy平面

将式(9)写为：

(10)

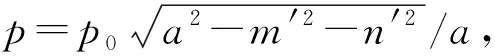
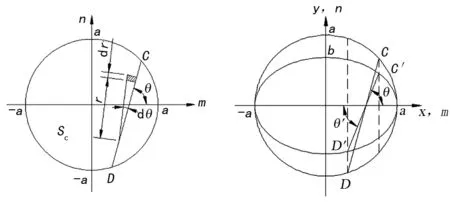
图4 圆形区域Sc的mn平面图5 坐标变换前后比对图

由图5可得：

l′cosθ′=lcosθ

(11)

(12)

由式(11)和式(12)可知:

(13)

(14)

(15)

弦长经坐标变化后为:

(16)

为了求出坐标变换前后的关系，需对式(15)两边求导

(17)

因此可得出:

(18)

将式(16)和式(17)代入式(10)，可得:

(19)

根据坐标变换关系如图6所示，可知：

l2=a2-(msinθ+ncosθ)2

(20)

经坐标变换后，p为半球面函数可写为：

(21)

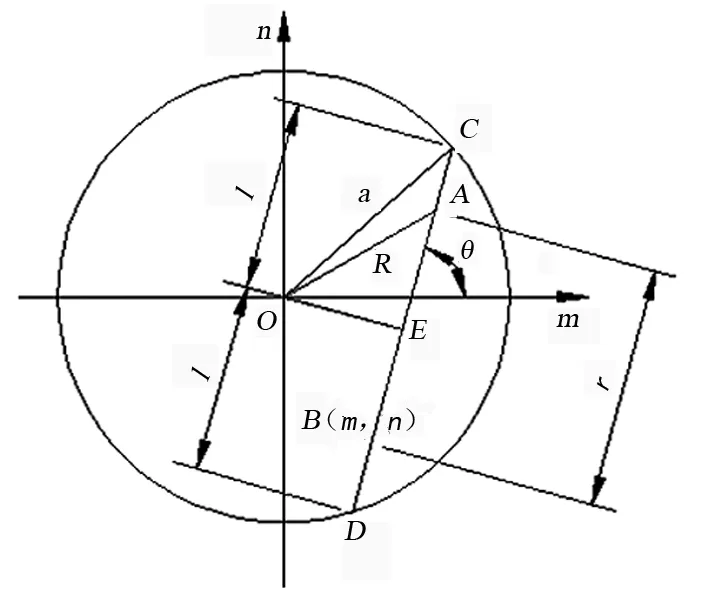
图6 坐标变换关系图

于是可得式(19)中的第二项积分为:

(22)

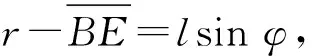
(23)

将式(23)代入式(19)可得:

(24)

将式(14)和式(20)代入式(24)得到:

(25)

令K(e)为第一类椭圆积分[6]:

(26)

L(e)为第二类椭圆积分：

(27)

e为椭圆偏心率：

(28)

对第一类和第二类椭圆积分进行组合，并令:

(29)

B(e)=K(e)-D(e)

(30)

根据式(26)～式(30)，可将式(25)改写为:

(31)

对变换坐标后的力平衡方程进行积分可得：

(32)

(33)

3 辊筒有限元模态分析[7]

3.1 建模与处理

利用Solidworks2012软件建立辊筒和深沟球轴承的框架结构图，然后将模型文件导入Ansysworkbench中划分网格并定义约束和载荷并指定辊筒和轴承的材料，最后生成有限元动力模型。如图7所示。

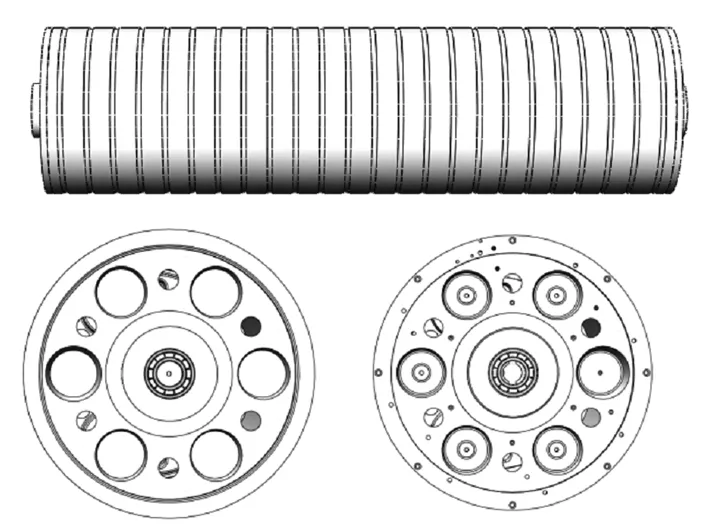
图7 辊筒和轴承组装动力学模型

模型在从SolidWorks转换到Ansysworkbench中为了保证尺寸一致，需要设定单位。定义mm为长度单位，kg为质量单位，N为力单位，s为时间单位。本工程采用的辊筒长为1 708 mm，直径为459.2 mm，轴承的宽度为18 mm，直径为80 mm。单位设置完成后，需要设定轴承和辊筒之间的接触设置，辊筒的内圈和轴承的外圈设为bond方式，轴承滚动体和内弯圈设为光滑无摩擦方式。根据Ansys中规定的面-面接触选定目标面和接触面原则，选定滚动体表面作为接触面，轴承内外圈表面为目标面。

3.2 材料参数

辊筒的材料采用铝合金6061 T6的材料，其弹性模量为软件默认的7.1×104MPa，密度为2.77×103kg/m3，泊松比为0.33。轴承的材料采用高碳铬轴承钢，弹性模量采用2.0×105MPa，密度采用7.85×103kg/m3，泊松比采用0.3。

3.3 载荷与边界条件的设置

采用Ansysworkbench软件设置轴承内圈的6个自由度位移为0，轴承中的滚动体轴向位移为0、径向位移为自由，x轴方向旋转自由、Y和Z轴方向的旋转自由度为0，指定全局坐标系，并划分网格。共划分节点数179 960个，单元数量98 598个。载荷、边界条件和网格划分如图8、9所示。

图8 滚珠和内圈的接触方式设置图9 辊筒和轴承组件的网格划分

4 运行与分析

通过Ansysworkbench软件分析自动列出矩阵方程，并计算出辊筒和轴承的位移变化和固有频率，并可以通过缩放比例来进行查看变形的位置。图10显示的是辊筒前6阶辊筒和轴承的位移分布云图和临界转速[8-9]的相关振型。

图10 辊筒和轴承组件前六阶模态振型

由于辊筒没有限制绕x轴旋转的自由度，所以第一阶的固有频率是刚体运动的固有频率，从第二阶的固有频率才开始转化为挠性体运动的固有频率。采用Ansysworkbench在辊筒恒定转速为300 r/min时静力分析结果，辊筒和轴承最大变形量只达到0.005 mm。将其与模态分析中的辊筒在共振时的位移量相比，共振产生的位移量明显增大。如表1所列。

表1 辊筒前六阶固有频率和最大变形量

第一阶固有频率5.3858 Hz转化为的转速则是5.3858×60=361 r/min，辊筒在323.15 r/min将发生共振，实际最大工作转速为270 r/min小于第一阶共振频率满足需求。若需提高工作转速增加打版的速度，则辊筒运行接近极限转速时，需加速运行以最短时间超出，辊筒仍可以正常工作，且不影响出版质量。