可实现参数化的渐开线圆柱齿轮建模方法研究*

2013-12-03张俊义丁文捷

机械研究与应用 2013年6期

张俊义，丁文捷

(1.宁夏工商职业技术学院，宁夏银川 750021； 2.宁夏大学机械工程学院，宁夏银川 750021)

1 引言

渐开线圆柱齿轮是机械传动系统中重要的传动零件，齿轮传动是一个复杂的运动过程，进行齿轮设计时需对强度、使用寿命和传动质量(冲击、振动、噪声)等因素综合考虑，采用人工完成上述工作，存在计算繁琐，设计周期长，效率低等问题[1]。如果能够建立一个精确的齿轮实体模型，便可基于各种机械类分析软件对齿轮的设计与校核进行分析研究。目前，已有的软件插件虽可对齿轮进行实体建模，但该实体模型一般是封装起来的，无法进行后续开发，一旦设计条件发生变化，齿轮模型还需重新构建。另外，在进行机械产品的快速设计过程中，齿轮模型要依据设计要求，随着机械产品整体及时作出调整，这就要求齿轮的实体模型必须可以实现参数化。

2 齿廓曲线组成分析

rf为齿根圆半径，rb为基圆半径，计算公式如下：

rf=0.5m(z-2ha-2c*)

=0.5m(z-2.5)

rb=0.5mzcosα

式中：正常齿：ha=1，c*=0.25；α为压力角，取20°。

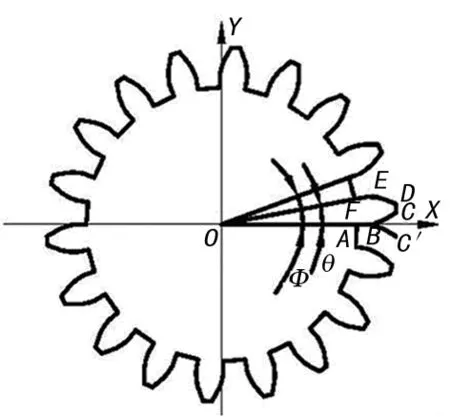
当rb>rf时，齿数z<41.4543。当齿数z≤41时，齿根圆包含于基圆，齿廓曲线必然由径向直线和渐开线两部分组成，且齿廓曲线处于基圆与齿根圆之间的为径向直线，处于基圆与齿顶圆之间的为渐开线；当rb

3 齿廓曲线绘制过程

基于上述对齿廓曲线组成的分析，在绘制渐开线圆柱齿轮齿廓曲线草图时，应按照齿根圆与基圆的包含情况分为两类进行讨论。为准确描述齿廓曲线的绘制过程，在一假定已绘制完成的渐开线圆柱齿轮齿廓曲线上建立如图1所示直角坐标系。

图1 置于直角坐标系中的齿廓曲线

由图1可知，单个齿的齿廓曲线可看作由AB、BC、CD、ED、FE五部分组成，其中AB、FE为径向直线部分，BC、ED为渐开线部分，CD为齿顶圆部分。下面以齿根圆包含于基圆的情况来分析齿廓曲线的绘制过程，因为齿根圆包含基圆时，齿廓曲线全为渐开线，只是少了绘制径向直线的部分。

(1) 考虑AB、FE径向直线部分。A点为齿根圆上一点，B点为基圆上一点，则A、B两点的坐标为：

xA=rf=0.5 m(z-2.5)

xB=rb=0.5 mzcosα,yA=yB=0

式中：正常齿：ha=1，c*=0.25；α为压力角，取20°。

由上述坐标值可确定AB径向直线。至于FE径向直线，将在之后与ED渐开线合并为FD整体去考虑，此处先不做处理。

(2) 考虑BC渐开线部分渐开线的极坐标方程和直角坐标方程分别为：

对于BC渐开线部分，B点对应齿顶圆压力角αk的下限，此时rk等于基圆半径，αk=0；C点对应αk的上限，此时rk等于齿顶圆半径，即rk=ra=0.5m(z+2)，由极坐标方程，在齿数z确定后，便可获得αk的上限。需要指出的是αk的下限是精确的，因此，可以保证与径向直线AB很好的衔接(即渐开线上的B点与径向直线上的B点重合)。而对于αk的上限，考虑计算中存在的误差，可在其计算结果的基础上，适当地增大一些，留一些裕度，以避免与齿顶圆连接时出现间隙。将αk的上限与裕度之和根据绘图需要进行n等分，包括αk的下限，则一共可等间隔地获得n个αk值。对应的θk也可获得n个取值，由渐开线的直角坐标方程便可获得渐开线上n个点的坐标值，顺次连接n个点，即可获得BC渐开线部分。为得到FE和ED合成的齿廓曲线部分FD，先将BC按x轴对称确定BC′，与AB组成AC′，如图2所示。

图2 AC′部分齿廓曲线

(3) 考虑FD部分。将获得的AC′部分逆时针旋转θ角，即可得到到FE和ED合成的齿廓曲线部分FD。θ角的算法按如下公式计算：

式中：基圆上压力角αb=0。

基于SolidWorks由AC′绕原点旋转θ角获得FD时，由于组成AC′中的BC′是由BC通过镜像功能得到的，存在关联关系，因此，在AC′绕原点旋转之前必须先删除BC，否则会导致旋转失败。再按上述思路重新绘制AC部分，则齿廓曲线上AB、BC、FE、ED四部分全部获得，如图3所示。

图3 AB、BC、FE、ED四部分齿廓曲线

(4) 考虑CD部分。绘制齿顶圆便可得到CD部分，同时绘制齿根圆，以得到相邻齿间齿根圆弧线部分，将单个齿阵列z份，对草图修剪后，便可获得剪开线圆柱齿轮的齿廓曲线完整草图，如图4所示。

4 渐开线圆柱齿轮参数化建模

按照上述渐开线圆柱齿轮齿廓曲线绘制方法，在SolidWorks软件中建立一个基准3D模型，该模型不仅要实现尺寸的全约束，同时要保证参数的可驱动性，因为基准3D模型中包含的绘制信息表明了它的来源和生成方法，是建模修改和进化的重要依据[2]。驱动基准3D模型的尺寸参数均通过Excel电子表来获得，它拥有计算公式编辑、公式间组合和关联计算功能[3]。并将Excel电子表另存为XML表格格式，作为数据表使用。由该数据表实现的复算性可以在更改齿数和模数这两个基本参数后，实现运算过程中全部参数高效地完成自动修改。基于SolidWorks进行二次开发，编制VB程序组件，根据设计需要，在VB程序组件对话框中输入齿数和模数，由程序组件中的Spreedsheet控件调用XML数据表，数据表在接到齿数和模数修改信息后，立即复算获得驱动基准3D模型的所有参数[4-6]。程序组件作为中介，再利用数据表中各个尺寸参数来驱动渐开线圆柱齿轮3D模型，从而获得目标齿轮。3D模型、XML数据表及程序组件的关系如图5所示。