考虑库水可压缩性的拱坝动力响应分析

杨 柳，何蕴龙

(武汉大学水资源与水电工程科学国家重点实验室，武汉 430072)

1 研究背景

坝体－库水的耦合作用一直是大坝抗震分析的重要课题，尤其在近年混凝土拱坝修建越来越多的情况下，拱坝的抗震分析中流固耦合的影响更是不可忽视的重要内容。目前在实际工程计算分析中，据Westergaard［1］动水压力解析解提出的附加质量模型应用最为广泛。但附加质量模型不计坝体自身变形和坝体－库水动力相互作用的影响，本文通过考虑库水可压缩性的流固耦合模型的计算分析来对比附加质量法的适用性。

由于拱坝自身的复杂性，对于拱坝动水压力的研究比重力坝要晚，1961 年，Korsubo［2］通过将坝体简化为中心角为直角的圆柱体的一部分，将库水区域简化为扇形，得出了刚性拱坝在简谐地面运动的坝面动水压力的解析解。在坝库系统中，是否考虑库水的可压缩性一直是个有争议的课题，Chopra［3］的研究发现忽略水的可压缩性将导致显著的误差，会过低估计地震动水压力。日本学者畑野正［4］的试验说明动水压力和地震输入频率紧密相关。中美两国合作进行的现场试验研究未获得支持哪种模型的明确结论［5］。目前对其进行数值方法的研究仍有重要意义，随着计算工具和方法的发展，计算模型得到不断完善，考虑库水可压缩性的流固耦合方法是一种比较符合实际的先进方法。本文用在流固耦合方面较有优势的有限元软件ADINA进行分析，讨论库水可压缩性在计算过程中的影响。

2 计算方法与拱坝有限元分析模型

2.1 数值分析方法

当考虑水体的可压缩性时，以结构位移和流体速度势组成混合未知量，有限元方程如下，

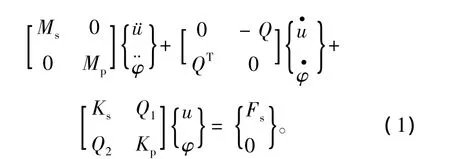
式中:［Ms］、［Ks］、［Fs］为与结构有关的质量、刚度和荷载矩阵;［Mp］、［Kp］为与流体相关的“质量”、“刚度”矩阵;Q为流固交界面上的耦合矩阵，Q1，Q2为与流体流速有关的耦合矩阵。

在可压缩库水模型中假设库水是均匀、无黏、无旋、线性小扰动理想流体，其基本方程表示为:

式中:▽2为Laplace算子;为水中声速;k为水体体积弹性模量;ρ为流体密度;φ为流体速度势(ν=▽φ，ν是流体速度);p为流体压力;ui为时均流速的3个分量;n为坝库交界面的法线方向;r为足够远处边界的法线方向。

2.2 有限元分析模型

五嘎冲水电站位于贵州省马别河上游平塘河段，坝顶高程1 344 m，最大坝高105 m，坝顶弦长612.5 m。有限元计算模型中拱坝坝高105 m，坝基范围及下游均取1.5倍坝高，根据黄耀英［6］、李瓒［7］等人的研究结果，为充分反映水体的影响，水库长度向上游取3倍坝高。采用无质量地基模型进行计算。在可压缩库水流固耦合模型中，库尾设置为无穷远边界，库水表面设置为自由液面，考虑了自由面波的影响。附加质量模型中将坝面上的动水压力施加到坝面节点上，其中材料参数:坝体体积弹性模量为20 GPa，密度为 2 400 kg/m3，泊松比为0.167，基岩体积弹性模量为25 GPa，泊松比为0.25，水体密度为1 000 kg/m3。模型如图1所示。

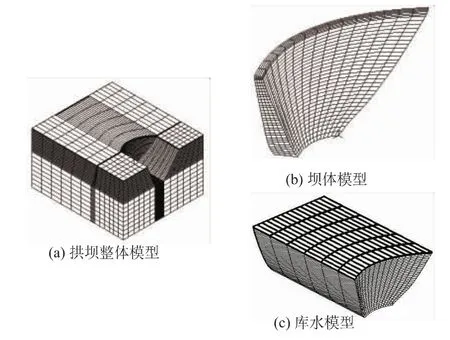
图1 五嘎冲拱坝模型Fig.1 Model of the Wugachong arch dam

2.3 地震波的选取

选取水工建筑物抗震设计规范推荐的标准反应谱为目标谱，生成人工地震波作为拱坝坝基输入地震波，地震加速度峰值为0.1 g，地震动反应谱特征周期为0.20 s，相应地震基本斜度为7度。图2为所输入的规范波的顺河向加速度时程曲线。

3 坝体自振频率和振型的分析

表1为2种模型的坝体自振频率，由于附加质量的影响，体系的质量增加而刚度未变，其自振频率在初期时下降幅度更大。从第1阶自振频率来看，相对于考虑库水可压缩性情况下的坝体自振频率，附加质量模型降幅达到17.38%，其后高阶频率中二者相差范围缩小，但整体上来说附加质量模型比可压缩库水模型频率小，周期较长。

图2 顺河向地震波Fig.2 Time-history curve of seismic wave along the river direction

表2为空库、可压缩库水模型、附加质量模型前五阶振型的比较表，其中附加质量模型的振型和空库振型一致，对称性相同，可见可压缩库水模型更能反映坝库相互作用。

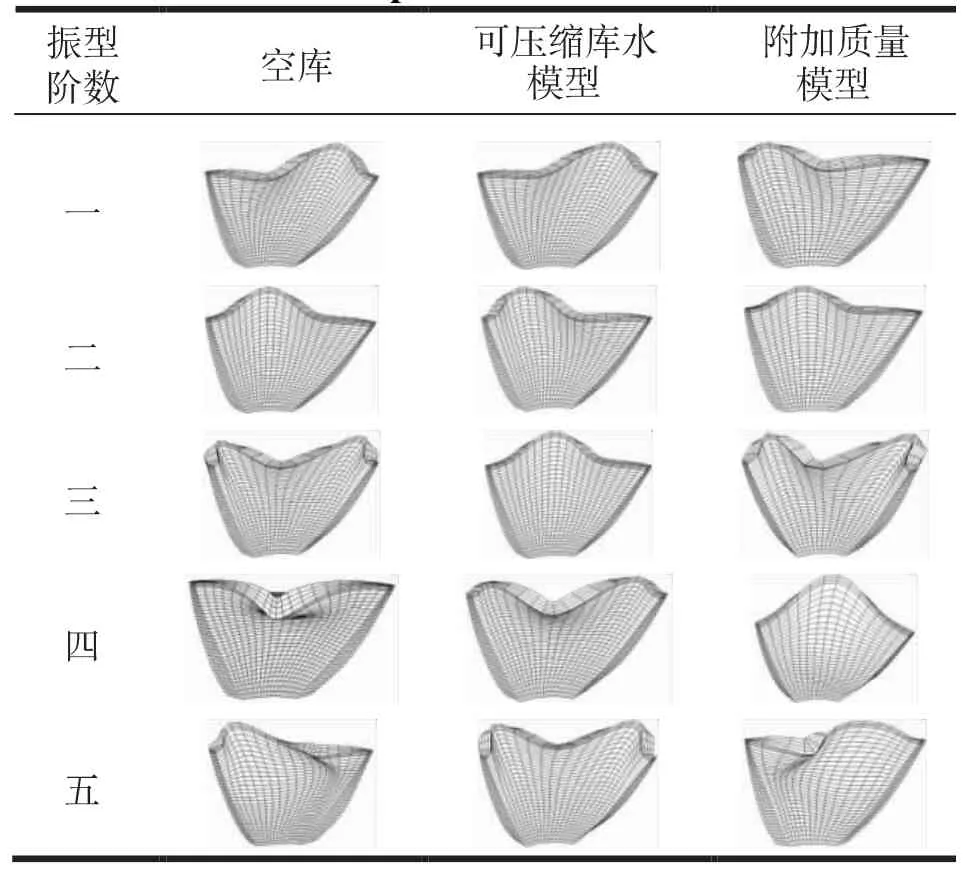
表2 振型比较Table 2 Comparison of vibration modes

4 拱坝地震动力响应分析

4.1 动水压力分析

图3分别为地震作用下2种模型拱坝上游面的动水压力包络图，可压缩库水模型的动水压力包络图如图3(a)所示，附加质量模型的动水压力包络图如图3(b)所示，在坝高1/3处达到最大，数值上近似是可压缩库水模型的2.5倍，与解析解所得结果相符合［8］。图4为2种模型坝高约15 m处同一点的动水压力时程图，可压缩库水模型最大值为93.78 kPa，在 10.0 s，附加质量模型最大值为165.86 kPa，在7.08 s。附加质量模型的动水压力在整个坝面比可压缩库水的动水压力大。

图3 动水压力包络图Fig.3 Envelopes of hydrodynamic pressure

图4 动水压力时程曲线Fig.4 Time-history curves of hydrodynamic pressure

图5(a)至图5(c)为各层沿拱圈的动水压力包络图，沿拱圈的法线方向表示动水压力的值，图中上部两条线分别表示可压缩库水模型和附加质量模型的动水压力值。可压缩库水模型的动水压力在每层拱圈中沿拱向变化不大，但各层拱圈的动水压力有所不同，附加质量模型的动水压力在每层拱圈的拱冠梁处达到最大，附加质量模型动水压力普遍大于可压缩库水模型的动水压力。在拱冠梁的动水压力包络图中，可压缩库水模型的动水压力随坝高的降低而增大，最大值出现在坝踵，为93.25 kPa，附加质量模型动水压力最大值出现在坝高1/3处，为217 kPa，在相同位置，附加质量模型的动水压力比可压缩库水的动水压力大152%.可压缩库水由于考虑了库水的可压缩性，更能真实模拟坝库相互作用。

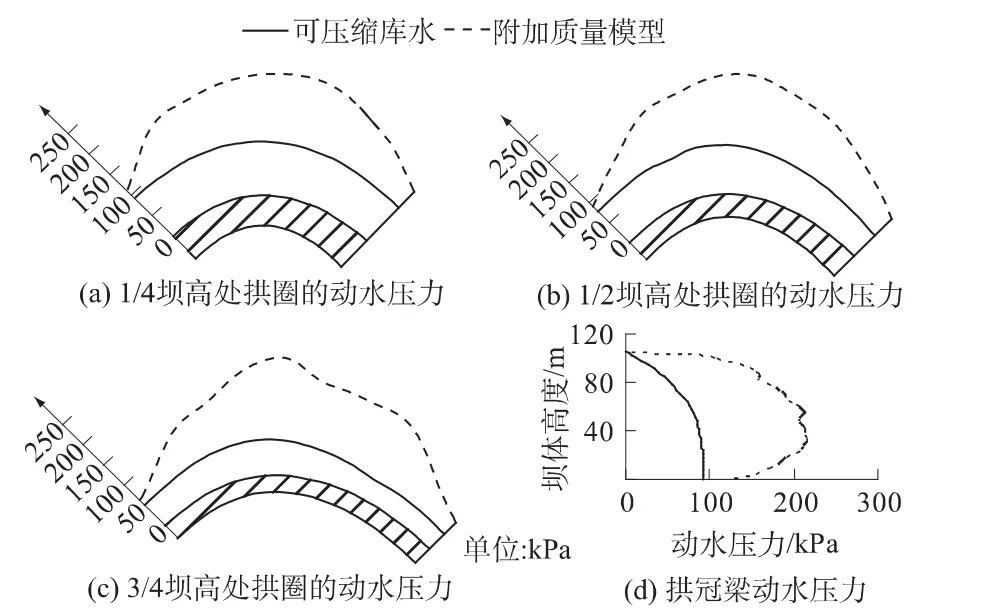
图5 各层拱圈及拱冠梁动水压力包络图Fig.5 Envelopes of hydrodynamic pressure in the arch and the crown cantilever

4.2 坝体位移变形分析

2种模型中坝体的位移变形规律基本一致，分别选取坝体拱顶、拱冠左右拱圈的特征点进行比较，各特征点的动位移比较如表3所示，可压缩库水模型和附加质量模型的动位移分布规律基本一致，横河向动位移最值出现在拱顶左1/4拱圈处，顺河向动位移和竖直向动位移最值出现在拱顶拱冠梁处。附加质量模型动位移结果几乎都比流固耦合模型动位移结果大。各方向位移时程曲线见图6。

表3 拱坝特征点动位移绝对值峰值Table 3 Maximum dynamic displacements of feature points

横河向位移时程(图6(a)):可压缩库水模型峰值发生在12.8 s处，为8.45 mm，附加质量模型峰值发生在9.9 s处，为8.27 mm，二者在整个时程中相差不大，改变周期相近。

顺河向位移时程(图6(b)):可压缩库水模型峰值发生在12.48 s处，为25.05 mm，附加质量模型峰值发生在9.5 s处，为29.34 mm，增大17.13%，库水可压缩性的考虑对顺河向位移影响较大。

竖直向位移时程(图6(c)):附加质量模型峰值发生在9.42 s处，为4.93 mm，可压缩库水模型峰值发生在10 s处，为4.90 mm，二者的位移均沿z轴负方向，发生时刻相近，峰值相差不大，但从整个时程图可看出，附加质量模型的竖直向位移比可压缩库水模型的竖直向位移大，在4～8 s中，二者相差不大，8～14 s中，附加质量模型的竖直向位移基本都比可压缩库水模型的结果大。

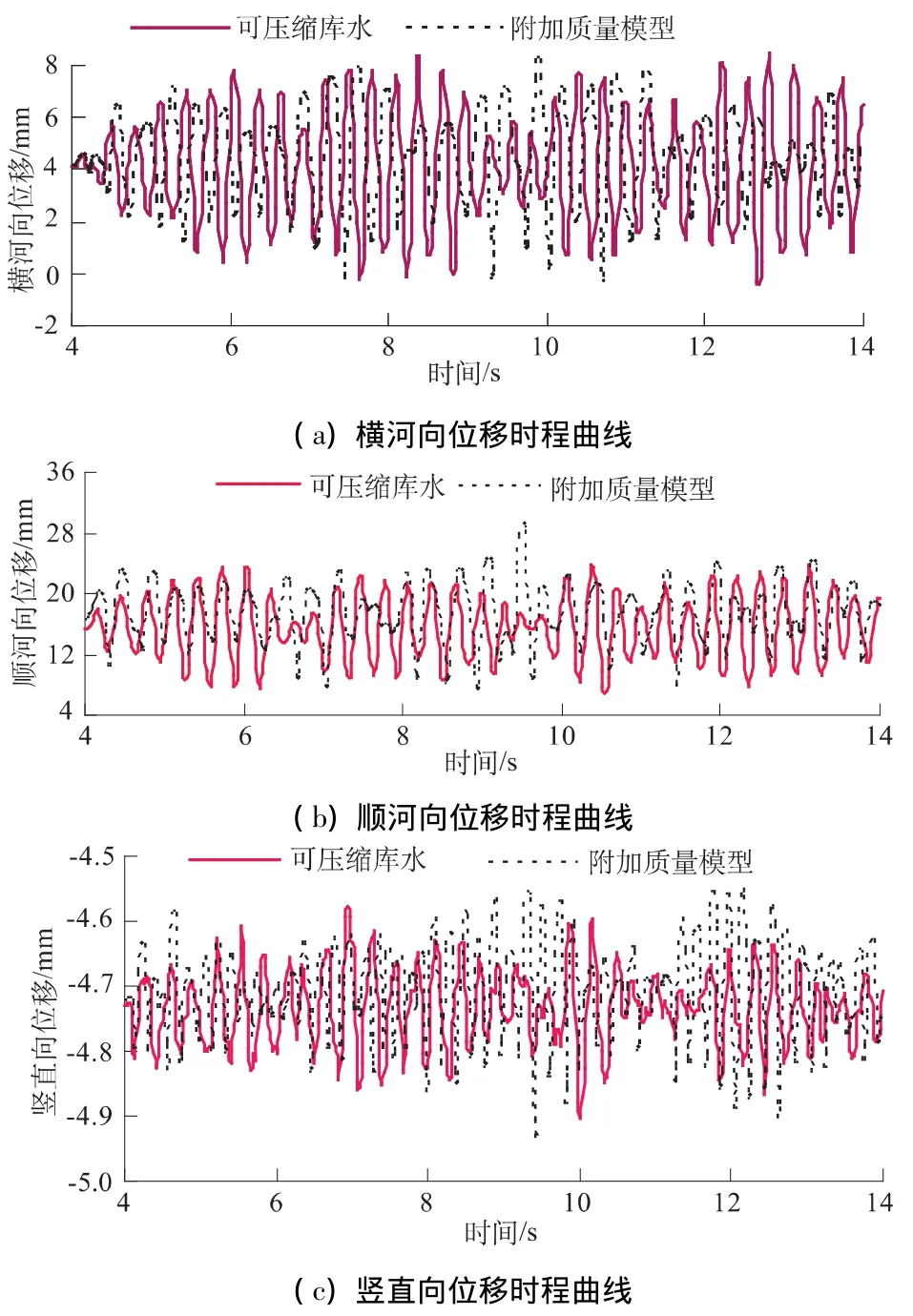
图6 各方向位移时程曲线Fig.6 Time-history curves of transverse，longitudinal and vertical displacements

由图7可得2种模型的顺河向绝对加速度时程规律基本一致且附加质量模型的顺河向加速度大于可压缩库水模型的结果，可压缩库水模型的峰值发生在12.50 s，为7.03 m/s2附加质量模型的顺河向加速度峰值发生在9.48 s，为7.88 m/s2，增大12.09%。

图7 顺河向加速度时程曲线比较Fig.7 Comparison of time-history curves of longitudinal acceleration

4.3 坝体拱向应力分析

可压缩库水模型和附加质量模型的拱向应力分布规律基本相同，上游面拱向拉应力最大值出现在坝肩处，可压缩库水模型的最大压应力出现在坝体上部拱冠梁处，附加质量模型的最大压应力出现位置接近坝顶，但分布趋势基本一致，2种模型的拱向应力相差不大(图8，图9)。

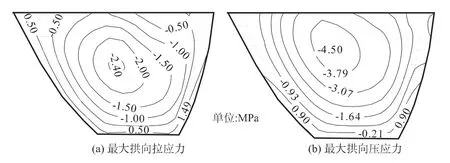
图8 可压缩库水的拱向应力的上游面动静叠加包络图Fig.8 Arch stress contours of upstream face of compressible fluid model after superposing the dynamic response

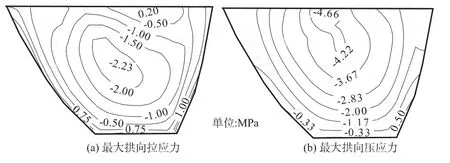
图9 附加质量模型的拱向应力的上游面动静叠加包络图Fig.9 Arch stress contours of upstream face of the additional mass model after superposing the dynamic response

4.4 坝体竖直向应力分析

图10 可压缩库水的竖直向应力的上游面动静叠加包络图Fig.10 Vertical stress contours of the compressible fluid model after superposing the dynamic response

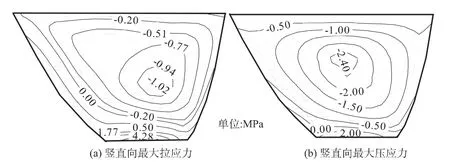
图11 附加质量模型的竖直向应力的上游面动静叠加包络图Fig.11 Vertical stress contours of the additional mass model after superposing the dynamic response

计算中压应力为负、拉应力为正。在图10和图11中(a)为静力计算的应力结果与拉应力的包络值叠加结果，(b)为静力计算的应力结果与压应力的包络值叠加结果。可压缩库水模型和附加质量模型竖直向拉应力的分布规律相同，拉应力出现在左岸坝肩及1/5坝高处以下，在坝体下部拉应力随坝高的降低而增大，最大值均出现在上游面坝踵处，可压缩库水模型的最大压应力为4.0 MPa，附加质量模型的最大压应力为4.3 MPa，增大7.5%。2种模型的压应力分布规律相同，压应力最大值出现在1/2坝高的拱冠梁处，可压缩库水模型的最大压应力为1.76 MPa，附加质量模型的最大压应力为2.40 MPa，增大36.36%。

5 结论

(1)从库水的物理特性来看，可压缩库水模型最能真实地反映库水的特性，也最能反映库水对坝体动力特性的影响。附加质量模型与可压缩库水模型相比降低了坝体的自振频率。

(2)2种模型的结果对比分析表明，附加质量模型的动水压力约为可压缩库水模型动水压力的2.5倍，当坝体受到顺河向地震激励时，由附加质量产生的动水压力会大大增大坝体的动力反应，与可压缩库水模型的计算结果相比，对顺河向位移反应影响较大，对竖直向位移影响较小，对横河向位移基本没有影响。对竖直向应力反应有较大影响，而对坝体拱向应力反应影响较小。

(3)地震激励作用下，附加质量模型计算的坝体的应力、位移反应比可压缩库水模型偏大，并且其误差在坝体上部更为明显，差别更大。附加质量模型夸大了地震时坝体的应力反应。

［1］WESTERGAARD H M.Water Pressure on Dams during Earthquakes［J］.Transactions of ASCE，1933，98:418 －472.

［2］KOTSUBO S.External Forces on Arch Dams during Earthquakes［J］.Memoirs Faculty of Engineering，1961，20(4):327－360.

［3］CHOPRA A K.Earthquake Analysis of Concrete Gravity Dams Including Dam-water-foundation Rock Interaction［J］.Earthquake Engineering ＆ Structural Dynamics，1981，9(4):363－383.

［4］畑野正.冢原重力ダムの振动实验とその考察［C］∥土木学会论文集.东京:日本土木学会，1958:8－16.(TIAN Ye-zheng.Analysis of Vibration of Zhongyuan Gravity Dam［C］∥Proceedings of Japan Society of Civil Engineers.Tokyo:Japan Society of Civil Engineers，1958:8－16.(in Japanese))

［5］CLOUGH R W，CHANG K T，CHEN He-qun，et al.Dynamic Interaction Effects in Arch Dams:Earthquake Engineering Research Center Report，No.UCB/EERC － 85/11［R］.Berkeley:University of California，1985.

［6］黄耀英，孙大伟，田 斌.两种库水附加质量模型的重力坝动力响应研究［J］.人民长江，2009，40(7):64－66.(HUANG Yao-ying，SUN Da-wei，TIAN Bin.Research on Dynamic Response of Concrete Gravity Dam in Two Types of Hydrodynamic Added Mass Dam Models［J］.Yangtze River，2009，40(7):64 －66.(in Chinese))

［7］李 瓒，陈兴华，郑建波，等.混凝土拱坝设计［M］.北京:中国电力出版社，2000.(LI Zan，CHEN Xing-hua，ZHENG Jian-bo，et al.Concrete Arch Dam Design［M］.Beijing:China Electric Power Press，2000.(in Chinese))

［8］王 忠，柴贺军，刘浩吾.重力坝动水压力与地震干扰频率的关系［J］.成都理工学院学报，2002，29(1):101 －104.(WANG Zhong，CHAI He-jun，LIU Hao-wu.The Relationship of Hydrodynamic Pressures on Structures with the Excitation Frequency［J］.Journal of Chengdu U-niversity of Technology，2002，29(1):101 －104.(in Chinese ))