微裂隙对工程岩体变形参数的影响分析

范 雷，姜 黎，胡启芳

（1．长江科学院水利部岩土力学与工程重点实验室，武汉 430010；2．中南电力设计院，武汉 430071）

微裂隙对工程岩体变形参数的影响分析

范 雷1，姜 黎2，胡启芳1

（1．长江科学院水利部岩土力学与工程重点实验室，武汉 430010；2．中南电力设计院，武汉 430071）

裂隙的大量存在使岩体的变形特性变得非常复杂，而在采用数值分析方法时，常常忽略微裂隙对岩体力学特性的影响。为了明确微裂隙对岩体变形参数的影响，通过变形等效原理，对含单一微裂隙的岩体的变形参数进行估算。计算结果表明：岩体的变形特性与微裂隙倾角、长度和荷载方向有关。微裂隙越长，岩体的变形模量越小，泊松比越大；微裂隙倾角与荷载方向的夹角越小，岩体的各向异性越明显，但是，随着夹角的增大，岩体不同方向上的变形模量逐渐减小，泊松比逐渐增大，岩体的各向异性逐渐减弱，当微裂隙与荷载方向的夹角为45°时，岩体则表现为各向同性。

岩石力学；微裂隙；柔度矩阵；变形参数

1 研究背景

岩体在各种各样的构造作用下产生了多种性质的裂隙，并且由于各种裂隙的大量存在，使得岩体的变形特性变得非常复杂。

随着数值模拟技术的日益强大，其在探讨分析裂隙岩体力学特性、破坏机理及合理准确确定裂隙岩体的宏观力学参数等方面的应用越来越广泛。例如，Kawamoto等基于有限单元法对节理岩体进行了等效连续研究［1－2］。何满潮根据室内完整岩块试验参数，结合野外工程岩体结构特点进行计算机数值模拟试验，给出了正交节理化岩体的试验结果［3］。盛谦、周火明等运用弹塑性有限元的数值方法研究了三峡船闸区典型地段的节理裂隙岩体宏观力学参数的结构效应［4－6］。唐辉明、张宜虎等采用有限单元法模拟了三维裂隙岩体等效变形参数［7］。Ki－Bok Min与Lanru Jing采用离散单元法对节理岩体进行数值试验研究后，提出了确定不连续岩体的等效弹性特性的方法［8－9］。李世海采用三维离散元模拟了含节理岩块的单轴压缩试验［10－11］。

对于贯通裂隙分布的岩体，采用上述有限元、离散元等数值方法已可较好地反映岩体的力学特性。但是对于存在未贯通微裂隙的岩体，由于微裂隙尖端应力场的奇异性，数值方法大多无法较好地模拟微裂隙尖端应力场。目前，在采用数值分析方法时，常常忽略微裂隙对岩体力学特性的影响。但是，这一做法是否合适，则有待商榷。针对这一问题，本文将对微裂隙对岩体变形参数的影响进行简单的探讨。

2 含单一非贯通裂隙岩体本构关系

裂隙岩体的变形主要是岩块、不连续面及充填物的总和，而后两者的变形起着控制作用。衡量岩体的变形特性常采用弹性模量、剪切模量、泊松比等指标。对于含无充填单一裂隙岩体，其变形将会呈现明显的各向异性。

如图1所示，岩块包含一条倾斜的非贯通裂隙，裂隙长度为2a，倾角为β。岩石材料的弹性模量为E0，泊松比为ν0，剪切模量为G0，则岩石的柔度矩阵为

根据胡克定律，所含裂隙单元体的本构关系为：

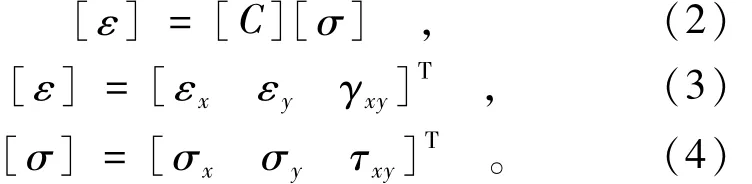
图1 含裂隙单元体Fig．1 Rock mass element containing one crack

对于任意方向的裂隙，根据坐标变换和叠加原理，可求得其对柔度矩阵的影响，即：

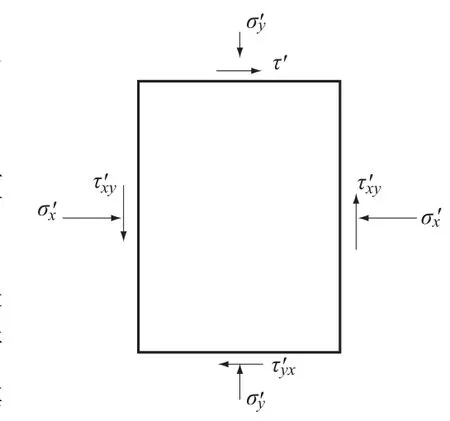
图2 等效无裂隙构元Fig．2 Equivalent rock mass element containing no crack

式中：［A］为几何矩阵Kn，Ks为裂隙面法向刚度与剪切刚度；Cn，C为裂隙面的传压系数和传剪系数［12］。

对于图1所示裂隙岩体等效为图2所示的无裂隙岩体时，等效后的岩体柔度比岩石柔度有所增加，根据各材料常数之间的关系，可对含非贯通裂隙岩体的变形参数进行估算。

对于传压系数，其确定可参考文献［13］，其表达式为

其中，对于平面应变状态，k＝3－4v；对于平面应力状态，k＝（3－v）／（1－v）。

对于传剪系数，当裂隙面剪应力τ小于其临界剪应力τm时，裂隙面不会产生相对位移，该裂隙面传递全部剪应力，则传剪系数Cs＝1；当裂隙面剪应力τ大于其临界剪应力τm时，此时裂隙面传递的剪应力为τm，传剪系数为

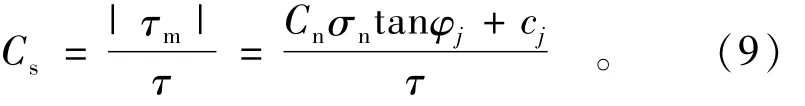
式中：φ为裂隙面内摩擦角；c为裂隙面内聚力。

3 算例分析

根据室内砂岩岩块和结构面力学试验，完整砂岩岩块变形模量为7．4 GPa，泊松比为0．25，结构面法向刚度为25．8 GPa／m，剪切刚度为12．9 GPa／m。选取模型高度（2d）为0．3 m，保持模型高宽比为2∶1，因而宽度（2b）为0．15 m。

当a∶b＝1／4，2／4，3／4，4／4不同值时，分别计算当裂隙倾角β＝0°，15°，30°，45°，60°，75°，90°时，含单一非贯通裂隙砂岩柔度矩阵，如表1所示。

根据材料常数之间的关系，单裂隙砂岩岩块水平方向和竖直方向的变形模量及泊松比见表2，其随裂隙倾角β的变化如图3所示。

图3 含单裂隙砂岩变形参数随β的变化曲线Fig．3 Variations of deformation parameters of sandstone containing one crack w ith dip angleβof crack

根据表2及图3分析结果可得：

（1）随着裂隙倾角β的增大，砂岩的变形模量先减小后增大，并在β为45°时达到最小值，泊松比的则先增大后减小，并在β为45°时达到最大值。

（2）随着a／b值的增大，砂岩的变形模量和剪切模量逐渐减小，泊松比逐渐增大。

（3）当裂隙倾角β为0时，含单一微裂隙砂岩在水平方向的变形模量和泊松比与完整岩块相同，但在竖直方向其变形模量和泊松比均有所降低。

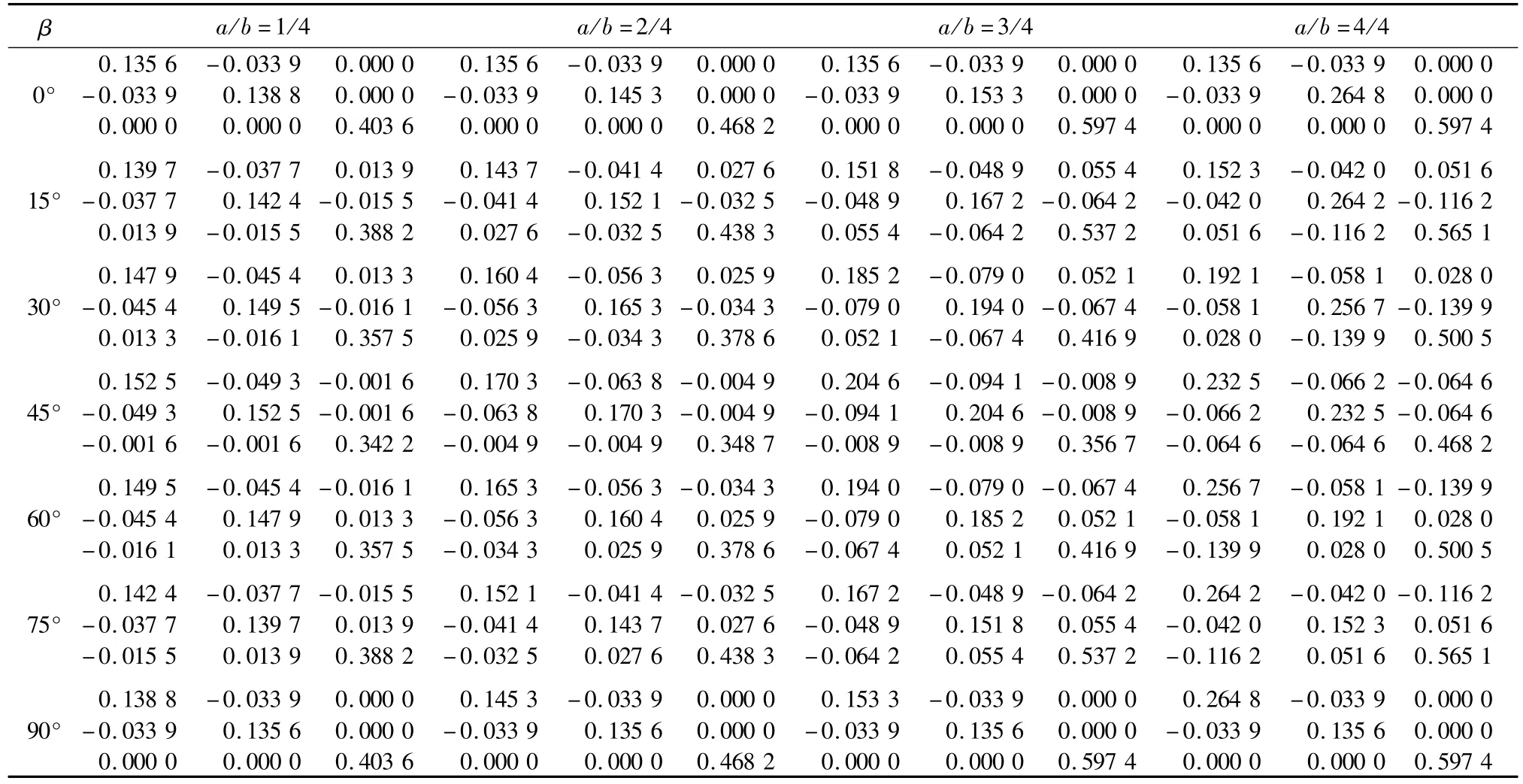
表1 含单裂隙砂岩柔度矩阵Table 1 Flexibility matrix of sandstone containing one crack

表2 含单裂隙砂岩变形参数Table 2 Deformation parameters of sandstone containing one crack

（4）当裂隙倾角为45°时，砂岩水平向和竖直向的变形参数相同，含单一微裂隙砂岩表现为各向同性。

（5）含单一微裂隙砂岩的剪切模量关于β＝45°对称，并且当β＝45°时达到最大值。

综上所述，可以发现含单一微裂隙的砂岩的变形特性与微裂隙倾角、微裂隙的长度和荷载方向有关。微裂隙越长，岩体的变形模量越小，泊松比越大。微裂隙倾角与荷载方向的夹角越小，岩体的各向异性越明显，随着夹角的增大，岩体不同方向上的变形模量逐渐减小，泊松比逐渐增大，但岩体的各向异性逐渐减弱，当微裂隙与荷载方向的夹角为45°时，岩体则表现为各向同性。

4 结 论

（1）含单一微裂隙岩体的变形特性与微裂隙倾角、微裂隙的长度和荷载方向有关。

（2）微裂隙越长，含单一微裂隙岩体的变形模量越小，泊松比越大。

（3）微裂隙倾角与荷载方向的夹角越小，岩体的各向异性越明显，当微裂隙与荷载方向的夹角为45°时，岩体表现为各向同性。

参考文献：

［1］ KAWAMOTO T，ICHIKAWA Y，KYOYA T．Deformation and Fracture Behavior of Discontinuous Rock Mass and Damage Mechanics Theory［J］．International Journal for Numerical and Analytical Methods in Geomechanics，1988，12（1）：1－30．

［2］ KAWAMOTO T A．Modeling of Jointed Rock Mass［C］∥Proceedings of the6th International Conference on Numerical Methods in Geomechanics．Innsbruck，Aprill 11－15，1988：24－32．

［3］ 何满潮，薛延河，彭延飞．工程岩体力学参数确定方法的研究［J］．岩石力学与工程学报，2001，20（2）：225－229．（HE Man-chao，XUE Yan-he，PENG Yanfei．A New Way of Determining Mechanical Parameters of Engineering Rock Masses［J］．Chinese Journal of Rock Mechanics and Engineering，2001，20（2）：225－229．（in Chinese））

［4］ 周火明，盛 谦．三峡工程永久船闸边坡岩体宏观力学参数的尺寸效应研究［J］．岩石力学与工程学报，2001，20（5）：661－664．（ZHOU Huo-ming，SHENG Qian．Size Effect Analysis on Macro-mechanical Parameters for the Rock Masses of Shiplock Slope of TGP［J］．Chinese Journal of Rock Mechanics and Engineering，2001，20（5）：661－664．（in Chinese））

［5］ 盛 谦，杨启贵，陈胜宏，等．节理岩体宏观力学参数的计算机模拟试验［J］．地下空间，1999，19（5）：482－487．（SHENG Qian，YANG Qi-gui，CHEN Shenghong，etal．Computer Simulation TestofMacro-mechanical Parameters of Jointed Rock Masses［J］．Underground Space，1999，19（5）：482－487．（in Chinese））

［6］ 盛 谦，黄正加，邬爱清．三峡节理岩体力学性质的数值模拟试验［J］．长江科学院院报，2001，18（1）：35－37．（SHENG Qian，HUANG Zheng-jia，WU Aiqing．Numerical Simulating Test on Joint Rock Mass Properties in Three Gorges Project［J］．Journal of Yangtze River Scientific Research Institute，2001，18（1）：35－37．（in Chinese））

［7］ 唐辉明，张宜虎，孙云志．岩体等效变形参数研究［J］．地球科学——中国地质大学学报，2007，32（3）：389－396．（TANG Hui-ming，ZHANG Yi-hu，SUN Yunzhi．A Study of Equivalent Deformability Parameters in Rock Masses［J］．Earth Science：Journal of China University of Geosciences，2007，32（3）：389－396．（in Chinese））

［8］ MIN K B，JING L．Numerical Determination of the E-quivalent Elastic Compliance Tensor for Fractured Rock Masses Using the Distinct Element Method［J］．International Journal of Rock Mechanics and Mining Sciences，2003，40（6）：795－816．

［9］ MIN K B，JING L，STEPHANSSON O．Determining the Equivalent Permeability Tensor for Fractured Rock Mass Using a Stochastic REV Approach：Method and Application to the Field Data from Sellafield，UK［J］．Hydrogeology Journal，2004，12（5）：497－510．

［10］李世海，董大鹏，燕 琳．含节理岩块单轴受压试验三维离散元数值模拟［J］．岩土力学，2003，24（4）：648－652．（LIShi-hai，DONG Da-peng，YAN Lin．3DDEM Numerical Simulation for Jointed Rock under Uniaxial Press Loading［J］．Rock and Soil Mechanics，2003，24（4）：648－652．（in Chinese））

［11］李世海，汪远年．三维离散元计算参数选取方法研究［J］．岩石力学与工程学报，2004，23（21）：3642－3651．（LIShi-hai，WANG Yuan-nian．Selection Study of Computational Parameters for DEM in Geomechanics［J］．Chinese Journal of Rock Mechanics and Engineering，2004，23（21）：3642－3651．（in Chinese））

［12］易顺民，朱珍德．裂隙岩体损伤力学导论［M］．北京：科学出版社，2005．（YI Shun-min，ZHU Zhen-de．Introduction to Fractured Rock Mass Damage Mechanics［M］．Beijing：Science Press，2005．（in Chinese））

［13］徐靖南，朱维申，白世伟．压剪应力作用下多裂隙岩体的力学特性——本构模型［J］．岩土力学，1993，14（4）：1－15．（XU Jing-nan，ZHU Wei-shen，BAI Shiwei．Multi-crack Rock Mass Mechanical Character under the State of Compression-Shearing-Constitutive Model［J］．Rock and Soil Mechanics，1993，14（4）：1－15．（in Chinese） ）

（编辑：赵卫兵）

Influence of M icrocracks on Deformation Parameters of Engineering Rock M ass

FAN Lei1，JIANG Li2，HU Qi-fang1
（1．Key Laboratory of Geotechnical Mechanics and Engineering of the MWR，Yangtze River Scientific Research Institute，Wuhan 430010，China；2．Central Southern China Electric Power Design Institute，Wuhan 430071，China）

A large number of cracks havemade the deformation properties of rockmass become very complex．However，the effect of thesemicrocracks is often neglected in the research of rockmass deformation properties using numerical simulation method．In order tomake clear the effect of thesesmicrocracks on the deformation parameters of rock mass，the deformation parameters of rock mass that contains one single microcrack are estimated based on

equivalent deformation principle．Results show that the deformation characteristics of rockmass are related with the dip angle，the length and also the load orientation of themicrocrack．When the length of themicrocrack is longer，the deformation module of the rock mass is smaller and the Poisson ratio is bigger．When the intersection angle between themicrocrack dip angle and the load orientation is smaller，the anisotropy of rock mass ismore evident．Whereas with the increase of this intersection angle，the deformationmoduli in different orientations are decreased，the Poisson ratios are increased and the anisotropy of the rock mass is weakened．When the intersection angle between themicrocrack dip angle and the load orientation is 45°，the rock masswill be isotropic．

rock mechanics；microcrack；flexibilitymatrix；deformation parameters

P642

A

1001－5485（2013）02－0027－04

10．3969／j．issn．1001－5485．2013．02．006

2011－09－14；

2012－02－01

国家重点基础研究发展计划（973计划）项目（2011CB710603）；中央级公益性科研院所基本科研业务费项目（CKSF2011022／YT）；水利部公益性行业科研专项经费项目（201001008）

范 雷（1982－），男，河北保定人，高级工程师，博士，主要从事岩石力学试验方面的研究工作，（电话）027－82829013（电子信箱）fanchon1982＠126．com。