反演梯形渠道砼衬砌体表面温度的太阳辐射模型

孙杲辰，王正中，2，李 爽，杨晓松，肖 旻，安 元

(1.西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100;2.中国科学院寒区旱区环境与工程研究所冻土国家重点实验室，兰州 730000)

1 研究背景

水是生命的源泉，更是控制国家经济的命脉，而我国是一个农业大国，不管是在农业种植还是生长过程中都离不开水，自从改革开放以来，我国开始了全国的基础性大建设，灌区建设更是重中之重，但是众所周知我国是世界上第三大冻土国，不仅冻土范围分布广泛，而且影响极为严重，特别是在广大的北方季节性冻土区，渠道基土冻胀是引起衬砌渠道破坏的主要原因。为了更好更充分地利用水资源，近年来，国内外很多专家都对冻土区衬砌渠道进行了深入的研究，并得到了一系列的研究成果。如王正中教授经过理论推导和试验研究得出了冻土属于各向同性材料，并推导出了适用于各种断面形式的衬砌渠道冻胀力学模型;李安国进行了大U形渠道试验研究;李学军依据温度梯度理论，论述了大型U形混凝土衬砌渠道冻胀机理，运用原型观测结果，建立了大型U形混凝土衬砌渠道季节性冻融水热耦合的二维模型，建立了冻深、冻胀预测模型。王正中［1］等还利用线性回归的方法将昼夜变化的温度简化成静边荷载并进行了数值模拟，而且还进行了太阳辐射作用下渠道水、热耦合数值模拟分析。虽然以前的专家已经做了很多的研究，但是对于具体渠道表面的温度在太阳辐射作用下如何变化并没有做出详细的理论研究［2－3］。

太阳辐射作为地球外部的全球性能源，对地球表面及近地面处的温度场有着重要影响［4］。特别是对于处于季节性冻土区的渠道而言，在太阳辐射的作用下外界温度升高，渠道一些部位冻结土壤中的冰开始融化，而随着其日照方向和日照强度的降低其又凝结成冰，这种反复的冻融破坏致使渠道混凝土衬砌体脱落，衬砌板底部土体掏空，造成渠道输水效率降低。如此看来，研究太阳辐射对渠道衬砌体的作用及随着日照部位的不同、渠道各个高程不同部位衬砌体表面温度是如何变化有着重要的意义。

在以前的研究中，只是将太阳辐射作为一种稳态的荷载加入到渠道表面进行研究，而这与实际中存在很大差别［5］;而且已有的太阳辐射模型需要大量的统计数据和实测辐射量来计算，相对比较麻烦［6－9］。本文根据渠道不同部位衬砌体表面接受太阳辐射量不同、温度不同的基本规律，利用太阳辐射量之间相互平衡的关系，建立了通过太阳净辐射反演渠道衬砌体表面温度的一种简单实用的太阳辐射模型，并通过MATLAB编程方法，反演了渠道砼衬砌体表面几个特征部位表面的温度，为以后的渠道衬砌体表面温度的变化规律研究提供参考。

2 理论模型的建立

渠道混凝土衬砌体表明太阳辐射的能量有以下几部分组成，其辐射如图1所示。对于衬砌体表面的温度来说，只有在求出地面的净辐射R净才能反演出其温度。本文主要通过2种方法来求解地面净辐射R净。方法1，通过辐射量平衡计算地面净辐射R净;方法2，通过经验公式计算地面净辐射R净。

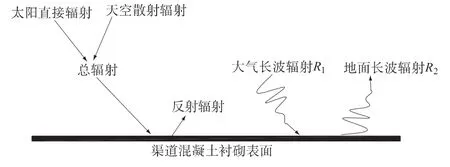
图1 梯形渠道衬砌体表面辐射计算简图Fig.1 Simplified diagram of calculating radiation on the lining surface of trapezoid canal

2.1 辐射量平衡地面净辐射计算

根据大气物理学的相关知识，地面净辐射R净由两部分组成，一部分为大气长波辐射，另一部分为地面长波辐射，其计算公式为

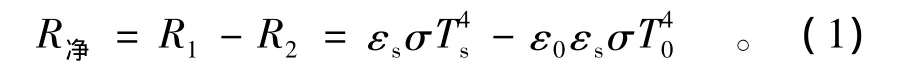
式中:R1为大气长波辐射;R2为地表长波辐射;εs为地表比辐射率，材料为混凝土时取0.88，沥青路面时取0.90;

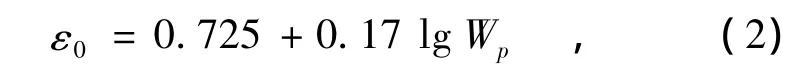
WP为可降水量;T0为大气温度;σ为Stefan－Boltman常数，σ =5.67 ×10－8W/(m2·K4);Ts为渠道混凝土衬砌板表面温度。

2.2 大气温度T0计算

因为在一天中大气温度会随着太阳的位置变化而改变，日照量是影响大气温度的主要因素，在本文大气日气温变化计算利用线性回归的方法，用公式(3)进行计算［10］，

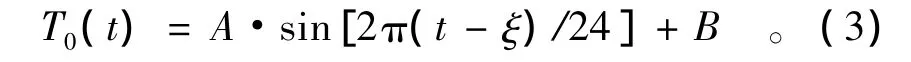
式中:A为日温度变化幅度;t为每日的小时数;B为日平均温度;ξ为太阳辐射日回归函数初相。

2.3 经验公式计算地面净辐射

地面净辐射除了利用(1)式中辐射量平衡的方法进行计算外;还可以依据很多经验公式，利用日照百分率s进行计算，此类公式主要有:Penman法、邓根云法、童宏良法等［11－14］。在这里主要介绍在1990年FAO的Penman-Monteith公式中，计算地表净长波辐射的公式:

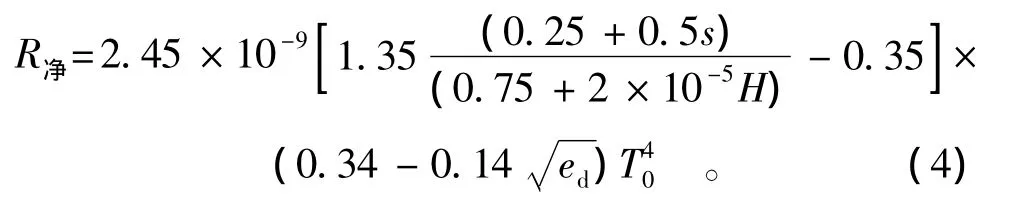
式中:H为海拔高度;ed为水气压;s为日照百分率。当(1)式和(4)式相等时便可得到反演混凝土衬砌板的温度公式为

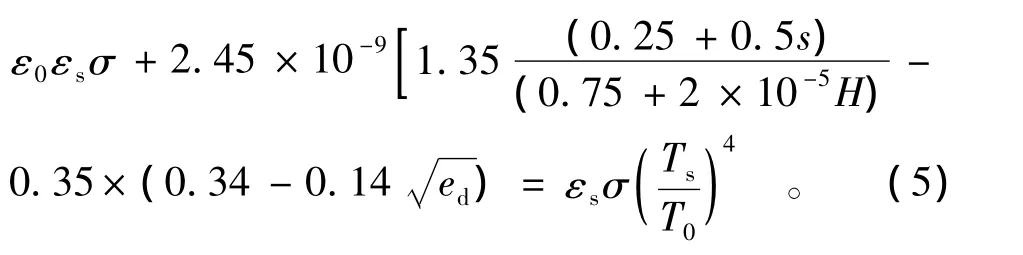
3 MATLAB程序流程

运用MATLAB编写太阳辐射下反演渠道混凝土表面温度程序，程序流程如图2所示。

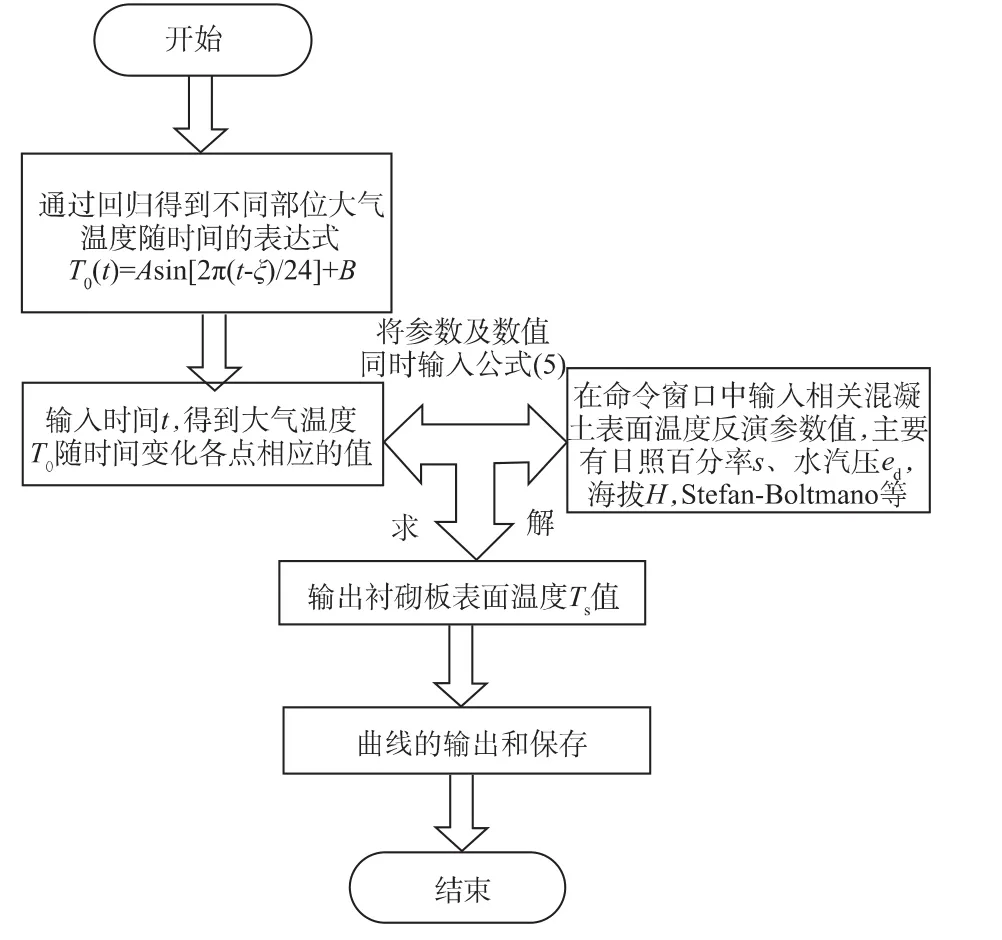
图2 MATLAB程序流程图Fig.2 Flow chart of MATLAB program

由以上程序图2可知，在计算时只要输入渠道混凝土表面相应的参数就可以得出渠道混凝土表面在每天24 h内任意一点温度随时间的变化值。

4 算例

如图3梯形渠道，其渠底高程H=520 m，一天内其温度的变换范围为－4～4℃，其中空气干燥没有降水，且阳坡、渠底、阴坡的日照百分率s分别为:s阳=30% ，s渠底=17% ，s阴=5% 。

(1)利用以上已知数据回归阳坡、渠底及阴坡的大气变化曲线。

图3 梯形渠道衬砌体图Fig.3 Section of the concrete lining oftrapezoidal canal

由公式(3)可知一天的大气温度变化，可以近似回归为一个正弦函数，由已知条件可知，渠道所在地其当天的温度变化范围为－4～4℃，由此可知其日温度的变化幅度A=8℃，日平均温度B=0℃，反算出其初相ξ=10，从而回归出阳坡的大气温度变化曲线，即

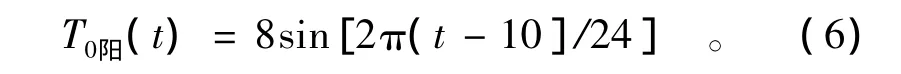
考虑到阴坡、渠底遮蔽的影响，渠底和阴坡的日照时间显然要比阳坡少，可以用阳坡的温度乘以地形系数。其中地形系数k为实际暴晒时间与理论暴晒时间的比值(朱伯芳1999)，由此可得阴坡的地形系数 k阴=0.113 6，k渠底=0.396。则阴坡的大气温度变化曲线为

渠底的大气温度变化曲线为

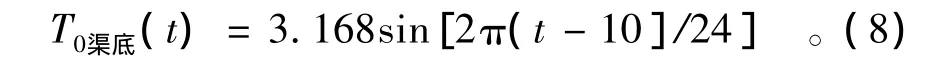
(2)利用MATLAB编程求解阳坡混凝土温度TS、大气温度T0与时间t变化曲线。

因为阳坡、渠底及阴坡的日照时间不同，其大气温度的分布也不同，近似的将阳坡看作在日出到日落时都接受阳光照射，则利用编程输出其阳坡衬砌板表面温度TS、阳坡大气温度T0随时间变化t的曲线，见图4。从图4中可以看出，阳坡的温度变幅较大，其相关数据如表1所示。

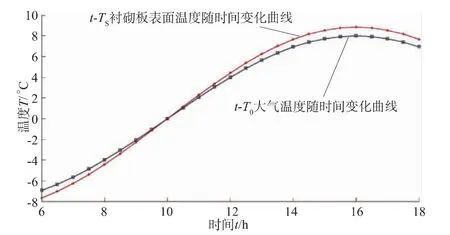
图4 阳坡温度T随时间t变化曲线Fig.4 Curves of sunny slope temperature T vs.time t

由表1中数据可知，阳坡混凝土衬砌板在日出时温度要比大气温度低0.731 4℃，但是随着日出后阳坡板接受太阳辐射量的增加，混凝土的温升速率明显要比大气的温升速率快，而且在下午16点左右达到其最高温度8.564 3℃，然后随着太阳辐射量的减少，其温度开始慢慢降低。

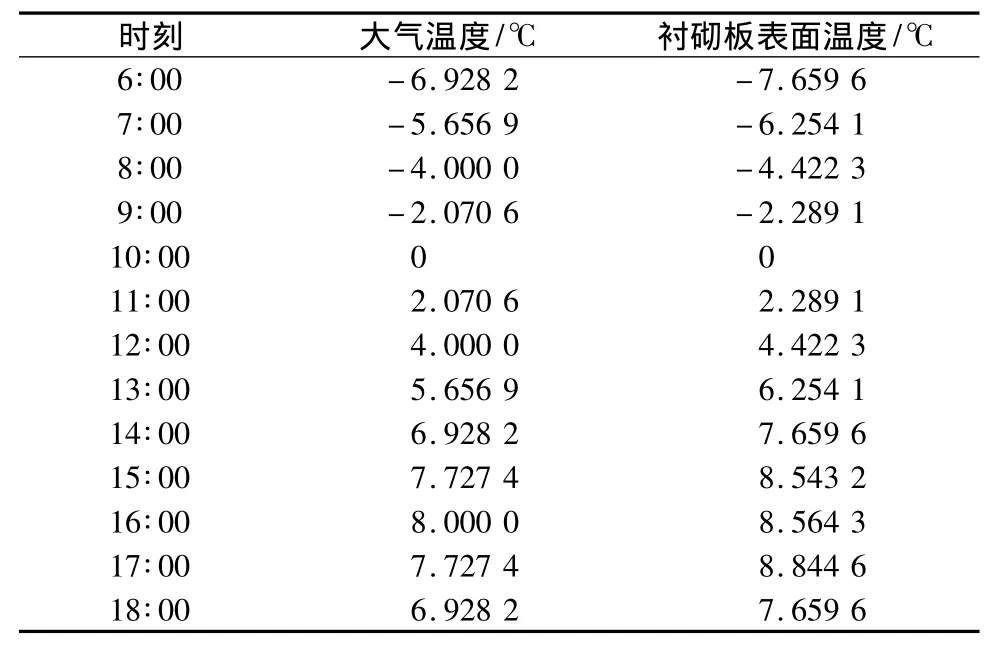
表1 阳坡各时刻大气温度与渠道衬砌板表面温度分布Table 1 Atmospheric temperature and temperature distribution on sunny slope of the lining surface at different times

(3)利用MATLAB编程求解渠底混凝土温度TS、大气温度T0与时间t变化曲线。

图5为渠底衬砌板表面温度TS、阳坡大气温度T0随时间t变化的曲线，其相关数据如表2所示。

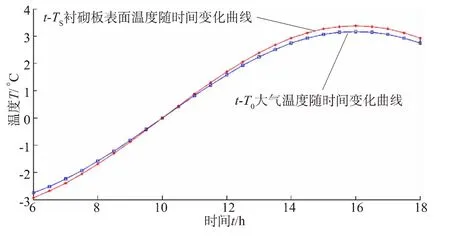
图5 渠底温度T随时间t变化曲线Fig.5 Curves of canal bottom temperature T vs.time t

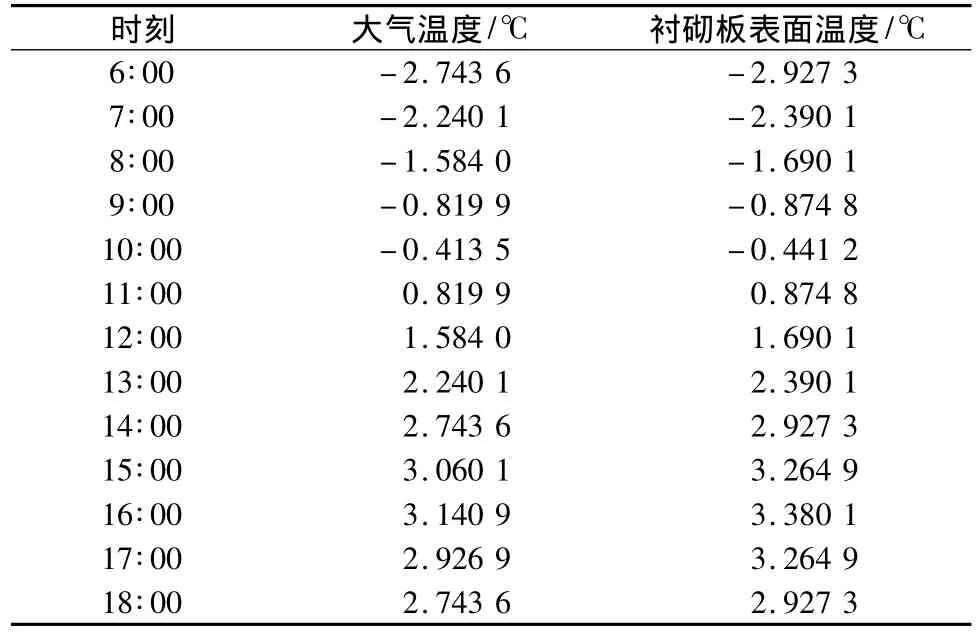
表2 渠底各时刻大气温度与渠道衬砌板表面温度分布Table 2 Atmospheric temperature on bottom of the canal and temperature distribution on the lining surface at different times

由以上的数据和图标可以看出，渠底与阳坡板接触点的砌板表面温度TS与阳坡大气温度T0随时间t变化的曲线的走势基本相同，但是由于其接受太阳辐射量的减小，其温度变化范围明显减小。与阳坡的温度变化范围相比，渠底的温度变化范围在－3～3℃之间，相比阳坡变化范围减少了25%，其大气温度最大值为3.140 9℃，衬砌板表面的温度最大值为3.380 1℃。

(4)利用MATLAB编程求解阴坡混凝土温度TS、大气温度T0与时间t变化曲线。

图6为阴坡衬砌板表面温度TS、阴坡大气温度T0随时间t变化的曲线，其相关数据如表3所示。

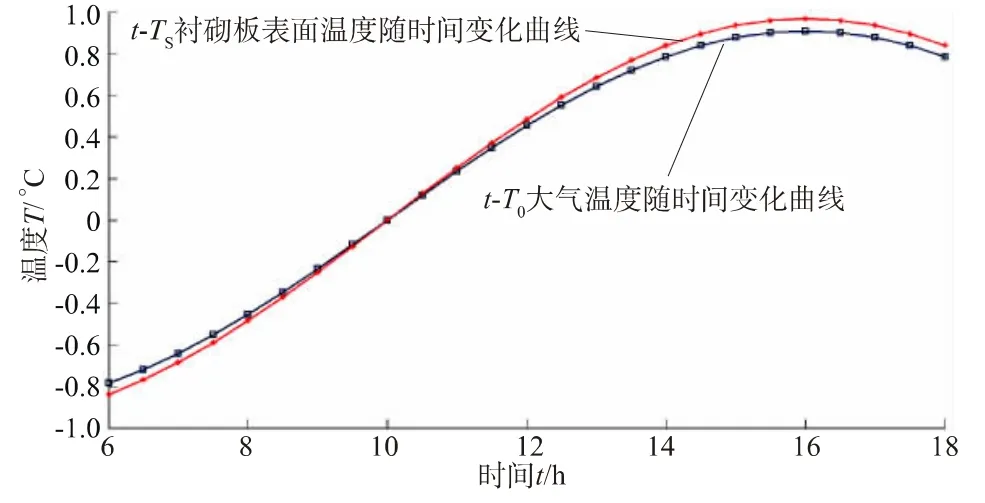
图6 阴坡温度T随时间t变化曲线Fig.6 Curves of shaded slope temperature T vs.time t

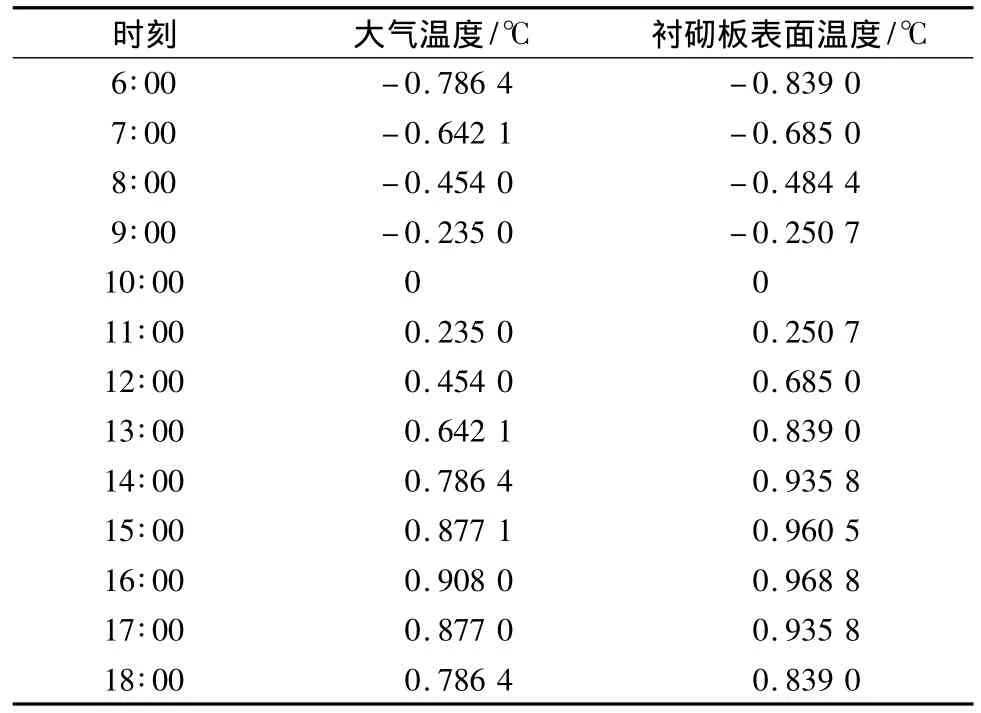
表3 阴坡各时刻大气温度与渠道衬砌板表面温度分布Table 3 Atmospheric temperature and temperature distribution on shaded slope of the lining surface at different times

由数据及图表可以看出，阴坡由于受到遮蔽等因素的影响其接受到太阳辐射总量减少，直接导致其温度变化范围急剧减小，与渠底和阳坡相比其温度变化范围基本上在－1～1℃之间，而且衬砌板表面的混凝土温升明显减小，其混凝土最高温度为0.968 8℃，大气温度为0.908 0℃，相比之下温升较慢。

5 结论

(1)本文通过分析太阳辐射对渠道衬砌板表面温度影响，利用地面净辐射多种公式之间的关系，建立了直接反演渠道混凝土衬砌板温度的太阳辐射模型，为以后的渠道混凝土衬砌板温度场数值模拟计算提供了一种更加精确的边界条件确定方法。

(2)计算结果表明，渠底、阴坡、阳坡的大气温度T0，以及衬砌板温度Ts随时间t变化的趋势一致，都是刚开始时衬砌板的温度相对于大气温度较低，随着大气温度的升高混凝土衬砌板表面的升温速率开始增加，并超过大气温度达到其最大值。

(3)虽然渠底、阴坡、阳坡的大气温度T0，以及衬砌板温度Ts随时间t变化的趋势一致，但其温度的变化范围存在很大的差异，阳坡由于接受太阳辐射较多较充足，其温度变化范围较大，渠底次之，阴坡最小。

(4)通过衬砌板温度与大气温度的比较可以看出，衬砌板温升相对于大气温升有一个滞后效应，在大气温度达到最大值时，混凝土衬砌板并没有达到最大值。

［1］王正中，芦 琴，郭利霞，等.基于昼夜温度变化的混凝土衬砌渠道冻胀有限元分析［J］.农业工程学报，2009，25(7):1 － 5.(WANG Zheng-zhong，LU Qin，GUO Li-xia，et al.Finite Element Analysis of the Concrete Lining Channel Frost Heaving Based on the Changing Temperature of the Whole Day［J］.Transactions of the CSAE，2009，25(7):1 －5.(in Chinese))

［2］王正中，芦 琴，郭利霞.考虑太阳热辐射的混凝土衬砌渠道冻胀数值模拟［J］.排灌机械工程学报，2010，28(5):455 －460.(WANG Zheng-zhong，LU Qin，GUO Li-xia.Numerical Simulation of Heave of Concrete Lining Channel by Taking Consideration of Radiation［J］.Journal of Drainage and Irrigation Machinery Engineering，2010，28(5):455 －460.(in Chinese))

［3］王大鹏，傅 智，房建宏，等.太阳辐射对青藏高原不同路面类型表面热状况及其下伏多年冻土的影响［J］.公路交通科技，2008，25(3):39 －43.(WANG Dapeng，FU Zhi，FANG Jian-hong，et al.Influence of Solar Radiation on Surface Thermal Regime of Different Pavement Types and Its Permafrost Underlying Embankment on the Qinghai-Tibetan Plateau［J］.Journal of Highway and Transportation Research and Development，2008，25(3):39 －43.(in Chinese))

［4］丑亚玲，盛 煜，韦振明.多年冻土区公路路基阴阳坡温度及变形差异分析［J］.岩土力学与工程学报，2009，28(9):1896 － 1903.(CHOU Ya-ling，SHENG Yu， WEI Zhen-ming.Temperature andDeformation Differences Between Southern and Northern of Highway Embankment on Permafrost［J］.Chinese Journal of Rock Mechanics and Engineering，2009，28(9):1896 －1903.(in Chinese))

［5］FEILIZADEH M，SOLTANIEH M，JAFARPUR K，et al.A New Radiation Model for a Single-Slope Solar Still［J］.Desalination，2010，262(1/3):166－173.

［6］EVEEV E G，KUDISH A I.The Assessment of Different Models to Predict the Global Solar Radiation on a Surface Tilted to the South［J］.Solar Energy，2009，83(3):377－388.

［7］HOCAOGLU F O.Stochastic Approach for Daily Solar Radiation Modeling［J］.Solar Energy，2011，85(2):278－287.

［8］VIJAYAKUMAR G，KUMMERT M，CLEIN S A，et al.Analysis of Short-Term Solar Radiation Date［J］.Solar Energy，2005，79(5):495 －504.

［9］GUEYMARD C A.The Sun’s Total and Spectral Irradiance for Solar Energy Applications and Solar Radiation Models［J］.Solar Energy，2004，76(4):423 －453.

［10］杨 婧，刘志璋，孟 斌，等.基于MATLAB的太阳辐射资源计算［J］.能源工程，2011，(1):35 －38.(YANG Jing，LIU Zhi-zhang，MENG Bin，et al.Resources Calculation of Solar Radiation Based on MATLAB［J］.Energy Engineering，2011，(1):35 －38.(in Chinese))

［11］FORTIN J G，ANCTLI F，PARENT L E，et al.Comparison of Empirical Daily Surface Incoming Solar Radiation Models［J］.Agricultural and Forest Meteorology，2008，148(8/9):1332－1340.

［12］杨金焕，毛家俊，陈中华.不同方位太阳辐射量及最佳倾角的计算［J］.上海交通大学学报，2002，36(7):1032 － 1036.(YANG Jin-huan，MAO Jia-jun，CHEN Zhong-hua.Calculation of Solar Radiation on Variously Oriented Tilted Surface and Optimum Tilt Angle［J］.Journal of Shanghai Jiaotong University，2002，36(7):1032 －1036.(in Chinese))

［13］NIJMEH S，MAMLOOK R.Testing of Two Models for Computing Global Solar Radiation on Tilted Surfaces［J］.Renewable Energy，2000，20(1):75－81.

［14］乔艳丽，古松，唐艳鸿，等.青藏高原的散射辐射特征［J］.南开大学学报(自然科学版)，2008，41(3):69 －76.(QIAO Yan-li，GU Song，TANG Yang-hong，et al.Characteristics of Diffuse Radiation on the Qinghai-Tibetan Plateau［J］.Acta Scientiarum Naturalium Universitis Nankaiensis，2008，41(3):69 －76.(in Chinese))