裂纹尖端解析解与周边数值解联合求解应力强度因子

苏海东，祁勇峰，龚亚琦

(长江科学院材料与结构研究所，武汉 430010)

线弹性断裂力学(Linear Elastic Fracture Mechanics，简称 LEFM)［1］是断裂力学中最早、也是发展最完善的一个分支。它以线弹性力学为基础，将结构视为带有裂纹的弹性体来研究裂纹的扩展问题，其中，裂纹按受力和断裂特征分为3类:张开型(I型)、滑开型(II型)和撕开型(III型)。根据经典的弹性理论，在裂纹尖端附近的应力具有奇异性。Irwin在1957年提出了新的物理量——应力强度因子(Stress Intensity Factor，简称SIF)来表征裂纹特性，相应的有3类应力强度因子KⅠ，KⅡ和KⅢ。

计算应力强度因子的方法有解析法和数值方法，前者只适用于简单形状。目前基于网格的数值计算方法主要以有限元法为主，由于奇异性仅存在于裂纹尖端附近很小的局部区域，往往存在网格划分困难、收敛慢等问题。近年来出现的数值流形方法［2］和扩展有限元法［3］提出了裂纹在网格内穿过的技术，从而大大降低了网格划分的难度，后者还引入了裂纹尖端位移场的特殊函数以加快收敛性，但这些方法仍需进一步改进。本文基于数值流形方法，提出裂纹尖端的解析解与其周边数值解联合应用以求解应力强度因子的新方法。以下限于平面问题，仅讨论Ⅰ型和Ⅱ型裂纹。

1 应力强度因子的数值计算方法及其研究现状

建立如图1所示的裂纹尖端处的(r，θ)极坐标。以Ⅰ型(张开型)裂纹为例，根据经典的弹性理论，裂纹尖端的位移、应力渐近场为:

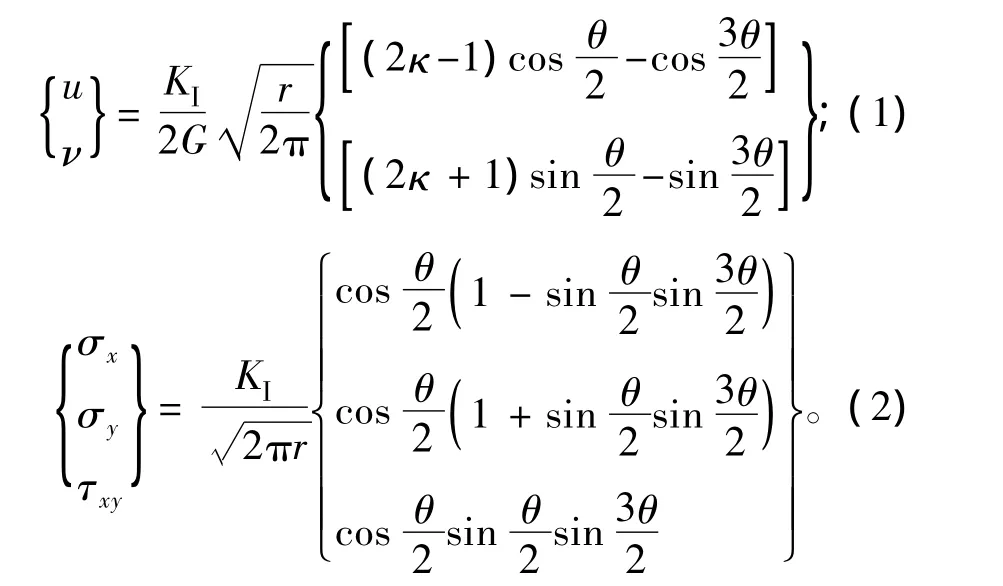
式中:

计算应力强度因子的方法主要有解析法和数值方法。复变函数、积分变换等解析方法一般只能求解简单形状的问题，而数值计算方法适用于复杂结构，包括目前应用最多的有限元法以及新兴的数值流形方法、扩展有限元法等。

图1 裂纹尖端附近应力分布Fig.1 Stress distribution near the crack tip

常规的有限元法要求在网格内使用连续函数作为插值函数，且材料性能一致，因此在处理裂纹这样的强不连续性问题时，一般要将裂纹尖点设置为单元结点，裂纹面设置为单元的边，为模拟裂纹尖端的奇异性需要布置非常细密的网格，而一旦裂纹发生扩展，需沿着裂纹扩展方向不断地修改单元网格和增加新结点，使用起来很不方便。

数值流形方法［2］(简称流形法)是石根华博士提出的一种新的计算方法，它引入两套覆盖(网格)体系:一是用于构造物理场近似解的数学网格;另一套是表示材料边界、用于定义积分区域的物理网格。两套覆盖体系相互独立，只要求前者在空间上完全包容后者。这样，材料的物理边界可以与数学网格不匹配，换言之，数学网格内可以有任意形状的材料体(称为流形元)。目前所见的流形法多采用有限元网格作为数学网格，在结点上采用级数表达式的覆盖函数(一般为多项式级数，也可以是其他类型级数甚至是解析解级数，未知量为级数的系数)，通过有限元网格的形函数(流形法中称为权函数)相连形成网格内的插值函数。当采用多项式覆盖函数时，一般应用单纯形精确积分法以保证数学网格内任意形状流形元的积分精度。为避免歧义，以下所述的“网格”均指数学网格。

对于不连续分析问题，流形法引入不连续覆盖来模拟裂纹［2］，如图2所示的具有1条裂纹的材料体，裂纹将网格分割成不连续的区域，每个区域称为一个物理覆盖，在裂纹的两边采用不同的覆盖编号，比如，结点覆盖7被裂纹分割成71和72，在网格7-8-13-12中，材料体被裂纹分割成两个流形元，裂纹下边的流形元覆盖为71-81-131-121，裂纹上边为72-82-132-122。这样，裂纹可以在网格内部穿过，巧妙地解决了常规有限元法裂纹面必须与单元边一致、裂纹扩展后需要重新划分网格的问题。但目前，流形法还难以处理裂纹尖端停留在网格中间的情况，如图2中的网格8-9-14-13。

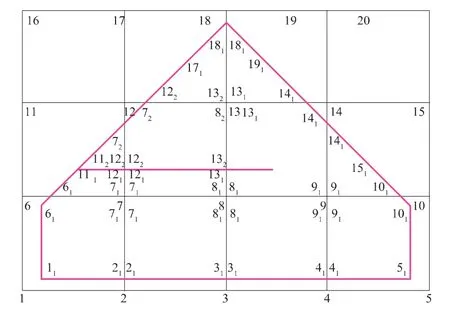
图2 有一条裂纹的材料体的矩形网格覆盖Fig.2 Rectangular meshes covering material domain with one crack

扩展有限元法［3］借鉴了流形法思想，裂纹同样可以在有限单元中穿过，对于裂纹尖端停留在网格中间的情况，在网格内引入附加基函数来扩展自由度，基函数一般取为裂纹尖端渐近位移场(见式(1))中的等以反映裂纹尖端的奇异性。反过来，也有流形法的相关文献［4］借鉴扩展有限元的这种方式处理裂纹尖端停留在网格中间的情况。

以上方法求解应力强度因子时，都需要通过计算裂纹尖端附近的位移或应力来推求应力强度因子，对位移或应力的精度要求高。实际上，有一种更直接的方法，利用裂纹尖端附近的Williams位移解析级数［5］直接求得应力强度因子。由于引入了与位移自由度不同的级数系数作为未知数，因此裂纹尖端附近的这种单元被称为杂交裂缝单元(Hybrid Crack Element，简称HCE)。该单元与周边以位移为自由度的常规单元的连接问题是该方法的研究重点，在常规有限元法的框架下，这种连接过渡是比较困难的，一般要采用特殊的网格划分［6］，或者如文献［7］提出的广义参数单元。

流形法具有解析解和数值解联合应用的方便性，作者曾在文献［8］中应用这种特性很好地求解了带有特殊无限域流场的流固耦合问题。本文沿用这种思路，运用裂纹尖端附近的Williams解析解与周边数值解联合求解应力强度因子。

2 裂纹尖端位移场的Williams级数解析解及其覆盖函数

如图1所示的裂纹尖端区域，Williams位移级数解为(裂纹边界满足无应力条件)

式中:

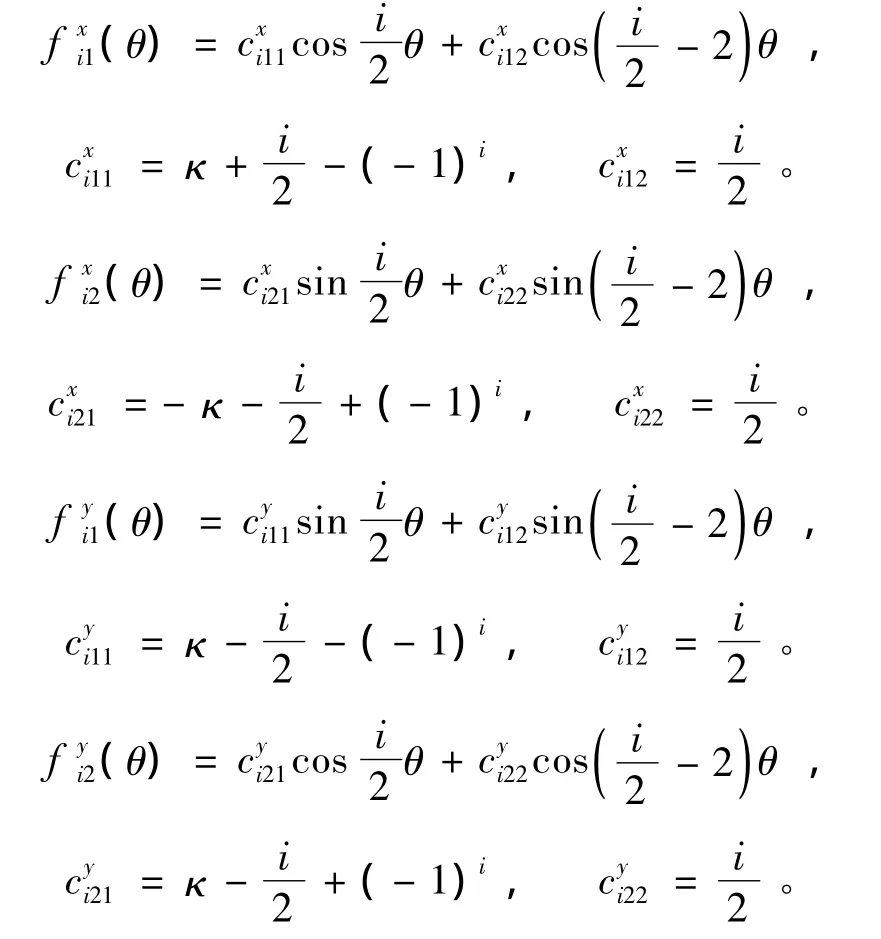
ai，bi为待求系数，其中a0，b0代表刚体位移项。应力强度因子与ai，bi的关系是

显而易见，Ⅰ型裂纹表达式(1)就是式(3)中取i=1，m=1及 bi=0的特殊情况。

如图3所示，在裂纹尖端所在的矩形网格6-7-11-10内，每个结点均采用式(3)的覆盖函数形式，并用矩形网格的形函数wj连接，形成网格内的插值函数，写成矩阵形式:

本文提出了采用结点自由度之间的强制约束方法，将该网格的结点7，11，10约束到结点6，即令，则根据形函数的关系，从而在该网格内形成独立的解析解覆盖

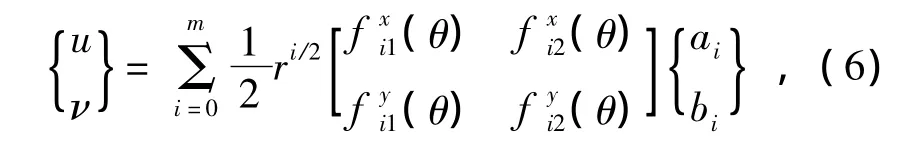
正好就是式(3)的矩阵形式。

以下推导应变矩阵和刚度矩阵。根据式(5)，应变子矩阵的第i项为

其中:

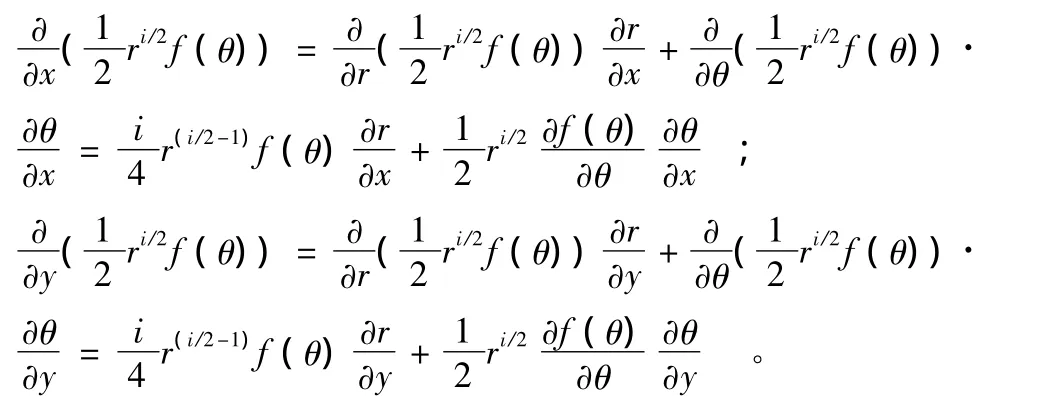
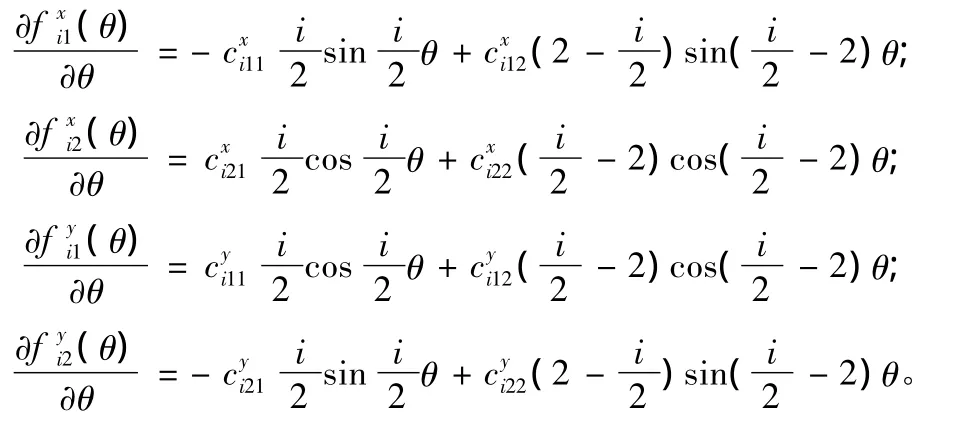
图3 裂纹尖端附近的矩形网格Fig.3 Rectangular meshes around the crack tip

另外:(x0，y0)为裂纹尖端坐标。

刚度子矩阵

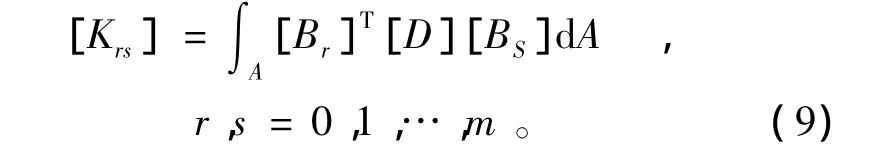
式中:［D］为弹性矩阵，A为流形元面积。

3 裂纹周边网格内的解析解与数值解的覆盖联系

除了裂纹尖端所在的网格外，在裂纹周边与该网格相连的其他网格内，位移统一表示为

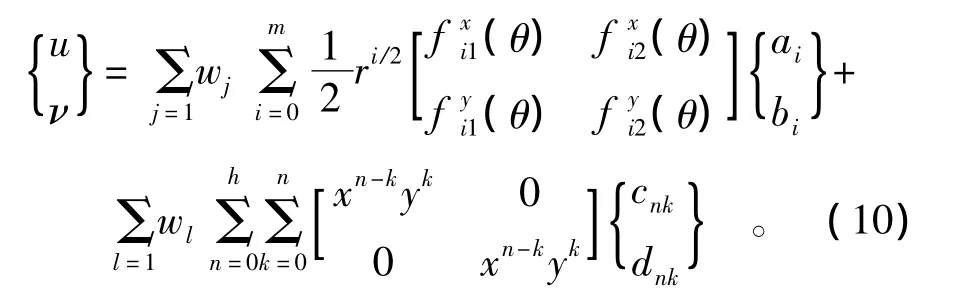
其中:cnk，dnk为待求的多项式系数;n，k为多项式阶次(h为多项式的最高阶次);wj，wl为相应于各结点的形函数;j和l的个数根据网格而定，但保持j+l=4。显然，取l=0则退化到解析解覆盖式(6)。

如图3所示裂纹周边网格，比如:网格3-4-8-7中的结点7为解析解覆盖，其它3个结点为数值解覆盖;网格7-8-12-11中的结点7和结点11为解析解覆盖(强制约束为同一覆盖函数)，结点8和结点12为数值解覆盖;网格5-6-10-9采用不连续的覆盖，实现裂纹两边的独立运动。

对于解析解覆盖结点j处的第i项，其应变矩阵为

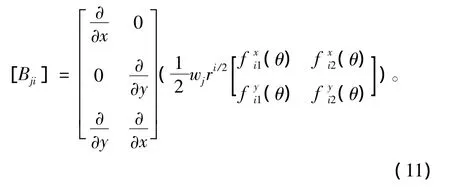
而对于数值解覆盖结点l处，第q项的应变矩阵为

解析覆盖与数值覆盖相关的刚度子矩阵为

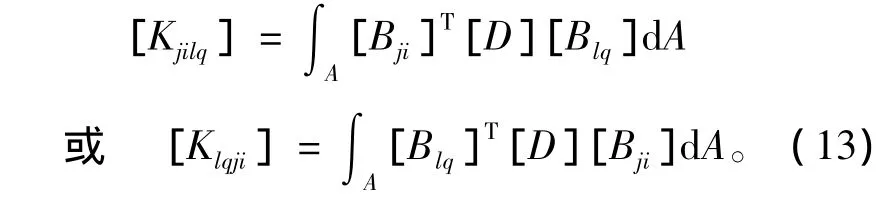
由式(7)至式(13)可见，刚度矩阵积分中具有非多项式的函数，因此基于多形式函数的单纯形积分公式无法应用。本文采用三角形区域的Hammer积分［9］，为保障数值积分的精度，考虑一种逐步的积分区域加密方式，如图2中的网格8-9-14-13中形成的流形元(见图4)，取其中心与流形元各边相连形成三角形积分区域即可进行Hammer数值积分，若积分精度不够，则在各三角形中，将边中点相连分解成4个小三角形，以此类推。一般而言，只需加密1次、最多2次就可以满足积分精度要求。

图4 积分区域加密Fig.4 Subdivided integration domains

4 算例

以无限长条为例，考虑以下几种典型裂纹。

4.1 两端受均布拉力的内部裂纹

如图5(a)所示，在宽度为B的无限长条中央有一条长度为2a的内部裂纹，长条两端受均布拉力p的作用。当4a＜B时，应力强度因子理论值［10］为取 a=0.05 m，B=0.8 m，p=0.3 kN/cm，则 KⅠ理论值为1.20。

4.2 两端受均布拉力的边界裂纹

见图5(b)，长条的宽度为w=0.4 m，其他同图5(a)，应力强度因子理论值［10］为其中，f(a/w)=1.12-0.23(a/w)+10.6(a/w)2-21.7(a/w)3+30.4(a/w)4，该算例中 KⅠ数值为1.45。

4.3 在裂纹嘴处受一对集中切向力作用的边界裂纹

如图5(c)所示，无限长条在其裂纹嘴处有一对集中切向力F=3 kN，其应力强度因子理论值［10］为，其中

该算例中KⅡ理论值为1.98。

流形元网格见图6，图6(a)为整体网格，图6(b)为裂纹附近的网格，网格尺寸为0.012 5～0.02 m，其中对于本文4.1节裂纹，考虑对称性取一半计算，对称面施加法向约束，图中横向粗线表示裂纹，竖向粗线为对称面，可见流形网格与物理边界不一致。而对于本文4.2节和4.3节的裂纹，在侧向不加法向约束。

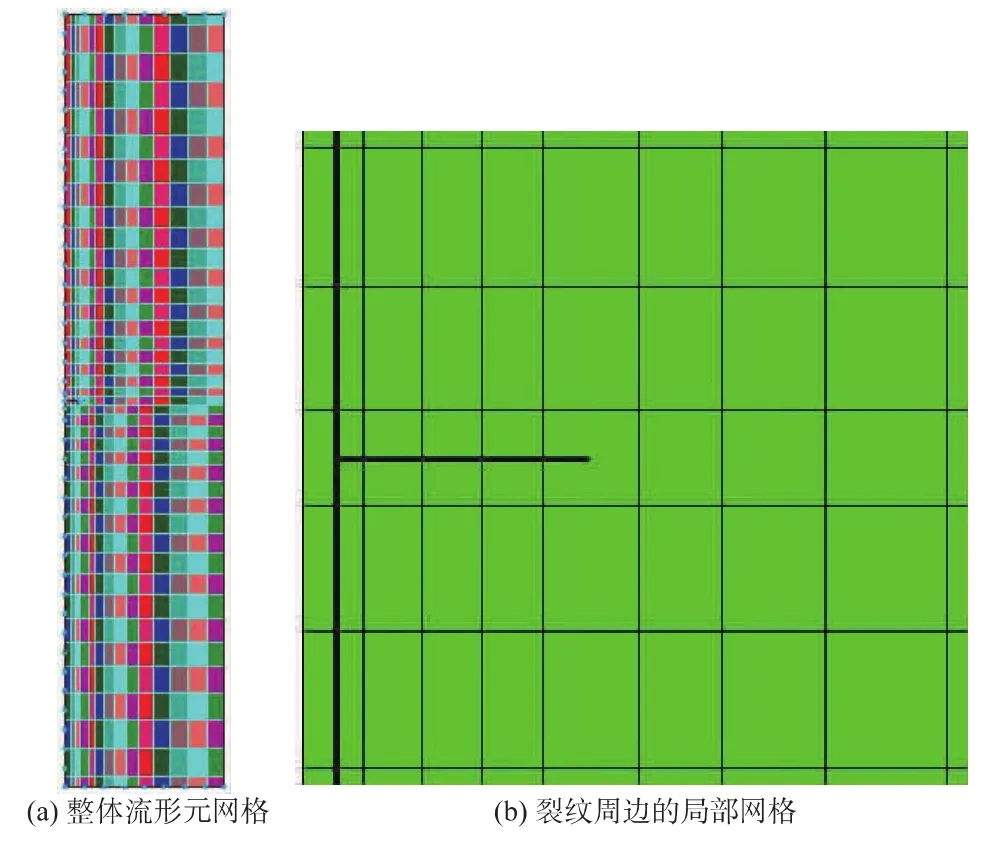
图6 流形元网格Fig.6 NMM meshes

对于两端受均布拉力的内部裂纹(本文4.1节)，应力强度因子KⅠ的计算结果见表1，随着Williams级数的阶数m以及周边数值解多项式函数最高阶数 n的增加，KⅠ的渐近值为1.23，与理论值1.20很接近。

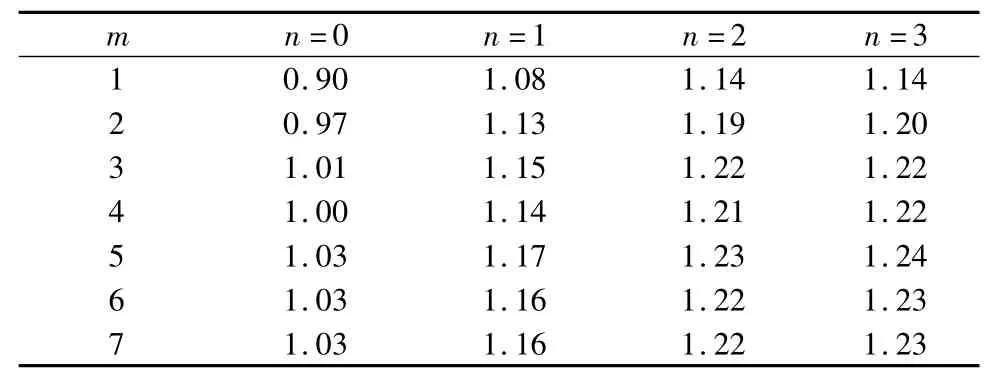
表1 应力强度因子KⅠ(两端受均布拉力的内部裂纹情况)Table 1 Stress Intensity Factor KⅠ(Two ends subjected to uniform tension，internal crack)

计算两端受均布拉力的边界裂纹(本文4.2节)，理论值为1.45，计算得到的 KⅠ渐近值也为1.45。

再计算边界裂纹受一对集中切向力的裂纹(本文4.3节)，理论值为1.98，计算得到的 KⅡ渐近值为2.00。

从以上计算结果可见，本文方法可以得到精度很高的应力强度因子计算值。以下对裂纹尖端附近的网格密度问题进行讨论。

如图7所示，将数学网格的尺寸加大，裂纹尖端附近的网格尺寸为0.03 ～0.05 m。对于两端受均布拉力的内部裂纹，应力强度因子KⅠ的计算结果见表2，可见计算精度明显降低，m至少取到7阶以上，KⅠ才能达到1左右。随着阶数的升高，计算也表现出一定的不稳定性，这表明本文方法对裂纹附近的网格密度仍有一定的要求，当网格密度不够时，计算结果不理想。至于如何判断是否达到理想的网格密度，这涉及到流形法的精度分析问题，需要更深入的研究。

图7 裂纹周边的局部流形元网格(粗网格)Fig.7 Coarse NMM meshes around the crack tip

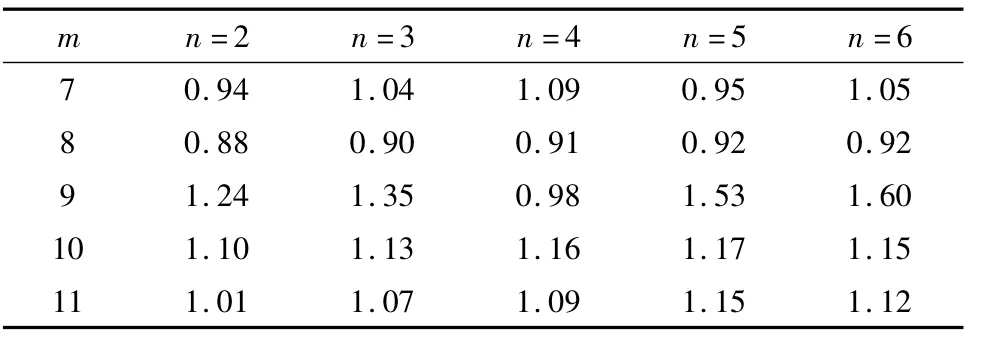
表2 应力强度因子KⅠ(两端受均布拉力的内部裂纹，粗网格)Table 2 Stress intensity factor KⅠ(Two ends subjected to uniform tension，internal crack，coarse meshes)

5 结语

由于裂纹尖端位移和应力分布的复杂性，用常规有限元网格的插值函数去逼近裂纹尖端的位移和应力是不易做到的，必须在裂纹尖端附近布置非常细密的网格。近年来发展起来的扩展有限元采用了裂纹尖端渐近位移场中的特征函数，能够比常规有限元插值函数更好地反映出裂纹尖端的奇异性，因而收敛较快。但扩展有限元只是使用了裂纹尖端渐近位移场的部分特征函数，而本文方法采用的Williams解析级数是对裂纹尖端位移场的最佳逼近，同时，周边数值解采用的高阶多项式插值函数相对于常规有限元和一般扩展有限元的普通插值多项式而言逼近的精度更高，因此本文方法收敛最快。

常规有限元和扩展有限元计算应力强度因子通常采用的“直接”法，需要通过裂纹尖端附近的位移或应力去拟合裂纹尖端的表达式进而推求应力强度因子;而所谓J积分的“间接”法，也需要在裂纹上、下表面定义的一个回线上进行积分，不同的回线得到的结果也会有差异。这些操作会引入额外误差。本文方法将应力强度因子作为方程组的未知数，不需要其他操作，是最“直接”最便利的方法，不会引入额外误差。

对于杂交裂缝单元(HCE)方法，虽然也是利用裂纹尖端附近的Williams解析解级数直接求应力强度因子，但这种单元与周边以位移为自由度的常规单元的连接过渡是比较困难的。在这一点上，本文方法具有较大的优势，流形法的不连续覆盖技术可以使裂纹在网格内穿过，这是常规有限元法以及在其框架下的HCE方法很难做到的。

综上所述，本文方法相比现有方法具有更快速的收敛性和更大的方便性。另外，对于流形法的研究而言，本文方法的意义在于:

(1)虽然流形法自诞生之时就以不连续覆盖的非连续变形分析方法而闻名于世，但如何处理裂纹尖端停留在网格内部的情况一直是其难以解决的问题，甚至落后于较晚出现的扩展有限元法，而本文方法成功解决了此问题。

(2)本文方法是继文献［8］之后的数值解和解析解联合运用的又一典型实例，再一次验证了梁国平教授在文献［2］的序中所述的“采用数值流形方法很容易就解决了人们多年来研究的至今尚未有好的解决办法的局部区域解析法以及有限元与解析法相结合的方法”，充分体现出流形法的优势。

本文方法虽然有更快的收敛性，但对裂纹尖端附近的网格密度仍有一定的要求，必要时需要加密网格。采用常规的网格加密方法，从普通大小的网格过渡到裂纹尖端处小一至两个数量级尺寸的网格是比较困难的。我们最近研究的部分重叠覆盖的流形法，可以方便地做到大小网格之间的协调过渡，非常适合于裂纹尖端的网格加密，将在另文介绍。

致谢:感谢数值流形方法的发明者石根华博士的指导。

［1］范天佑.断裂理论基础［M］.北京:科学出版社，2003.(FAN Tian-you.Basic Principle of Fracture［M］.Beijing:Science Press，2003.(in Chinese))

［2］石根华.数值流形方法与非连续变形分析［M］.裴觉民译.北京:清华大学出版社，1997.(SHI Gen-hua.Numerical Manifold Method(NMM)and Discontinuous Deformation Analysis(DDA)［M］.Translated by PEI Jue-min.Beijing:Tsinghua University Press，1997.(in Chinese))

［3］李录贤，王铁军.扩展有限元法(XFEM)及其应用［J］.力学进展，2005，35(1):5-20.(LI Lu-xian，WANG Tie-jun.The Extended Finite Element Method and Its Applications-A Review［J］.Advances in Mechanics，2005，35(1):5-20.(in Chinese))

［4］李树忱，程玉民.考虑裂纹尖端场的数值流形方法［J］.土木工程学报，2005，38(7):96-101.(LI Shuchen，CHENG Yu-min.Numerical Manifold Method for Crack Tip Fields［J］.China Civil Engineering Journal，2005，38(7):96-101.(in Chinese))

［5］WILLIAMS M L.On the Stress Distribution at the Base of a Stationary Crack［J］.Journal of Applied Mechanics，1957，24:109-114.

［6］KARIHALOO B L，XIAO Q Z.Implementation of HCE on a General FE Mesh for Interacting Multiple Cracks［C］∥Proceedings of the European Congress on Computational Methods in Applied Sciences and Engineering，ECCOMAS，Jyväskylä:July 24-28，2004.

［7］彭 俚.结构断裂分析的Williams广义参数单元［D］.南宁:广西大学，2008.(PENG Li.Williams Element with Generalized DOF for Structural Fracture Analysis［D］.Nanning:Guangxi University，2008.(in Chinese))

［8］苏海东，黄玉盈.数值流形方法在流固耦合谐振分析中的应用［J］.计算力学学报，2007，24(6):823-828.(SU Hai-dong，HUANG Yu-ying.Application of Numerical Manifold Method in Fluid-Solid Interaction Harmonic Analysis［J］.Chinese Journal of Computational Mechanics，2007，24(6):823-828.(in Chinese))

［9］王勖成，邵 敏.有限单元法的基本概念和数值方法［M］.北京:清华大学出版社，1988.(WANG Xu-cheng，SHAO Min.Basic Principle of the FEM and Numerical Method［M］.Beijing:Tsinghua University Press，1988.(in Chinese))

［10］中国航空研究院.应力强度因子手册［M］.北京:科学出版社，1993.(Chinese Institute of Aviation Research.Manual of Stress Intensity Factors［M］.Beijing:Science Press，1993.(in Chinese))