中心点法在岸坡稳定性分析中的应用

吴 锐，苏爱军，张 申，万 飞

(中国地质大学工程学院，武汉 430074)

1 研究背景

岸坡是指受水库蓄水影响的库岸斜坡岩土体［1］。由于水库对入库流量的调蓄作用，使水库岸坡的水环境发生了显著的变化:运行过程中库水位上下变动，改变了原来岸坡的地下水渗流场，加大了动、静水压力;水面的加宽、水深的加大、浪蚀作用的加强、岸坡再造的发生，改变了原有的库岸形态。水环境的改变使水库岸坡的水文地质条件、地应力和岩土体强度的变化均朝着不利于岸坡稳定的方向发展。因此，岸坡产生的新的变形，地质条件差的地带甚至发生崩塌、滑坡等地质灾害。水库蓄水后导致岸坡的变形和破坏常给人类工程活动及生命财产带来巨大的损失。

水库岸坡变形破坏与岸坡结构、岩土性状、岸坡的几何形态、水动力条件及水库运行过程中水位的波动等因素密切相关。岸坡变形破坏研究的目的，就是要作出科学的稳定性评价。这包括2方面的任务:一方面要对与工程活动有关的天然斜坡、已发生的滑坡、已建成的人工边坡的稳定性作出评价;另一方面要为设计合理的人工边坡和治理滑坡的措施提供设计依据。

通过我国的大量工程实践，总结出以工程地质分析为主的综合分析法，对岸坡均可以采用多种方法进行判断，并相互验证，达到科学分析的目的［2］。概况地讲，岸坡稳定性的评价方法可分为2大类，即定性评价和定量评价。定性评价方法包括成因历史分析法、工程地质类比法、赤平投影作图法等;定量评价方法包括极限平衡计算法、有限元分析法、破坏概率计算法等［3－4］。

在滑坡灾害的危险性分析和稳定性计算方法中，传统的确定性模型(条分法、推力传递法等)一直是将与稳定性有关的参数视为确定的参数。但是，大量的土工试验结果表明，即便是同一成因的岩土体，其物理力学参数也不是唯一确定的，而往往是服从某种概率分布［5］。

本文基于可靠度的分析，采用中心点法对核桃树沟滑坡进行稳定性分析计算，并与其它评价方法结果对比。

2 中心点法基本原理

中心点法的基本思想是:根据概率论中心极限定理，在状态函数为非线性的情况时，假定随机变量服从正态分布或对数正态分布，利用泰勒级数将状态函数在平均值处展开，并取一次项，在中心点附近取线性近似，对状态函数进行线性化处理，导出可靠度的解析表达式。

中心点法只适用于基本变量为正态分布，状态函数为线性的情况，而验算点法能考虑非正态基本变量，非线性状态方程，常用于基本变量为非正态分布时线性化处理时的验算。

本文基于可靠度的分析，采用中心点法推导出其理论计算公式，求得其可靠度指标、破坏概率及中值稳定安全系数，进行稳定性分析。

3 工程实例分析

3.1 滑坡概况

核桃树沟滑坡前缘宽度约90 m，平均宽度约100 m，滑体面积约8 500 m2，总体平面上滑坡为上窄下宽。主滑动方向为49°。滑带处于基岩强风化带顶部，深14 m，厚0.3 m，滑带组成物质为泥质粉砂岩;滑体中有挤压现象及滑带痕迹，滑体的成分为碎石土;花床为泥质粉砂岩。滑坡区位于扬子准地台扬子台褶带后缘，秭归向斜北东翼转折端，总体为向南西倾斜局部倒转的单斜构造;区内斜坡结构类型多而复杂，多为土岸和顺向坡及滑坡岸。岩层走向变化不大，倾向变化较大，断层不十分发育。

区内的地下水主要是基岩裂隙水和第四系孔隙水，水文地质条件受地层岩性和地质构造控制，香溪河对区内地下水的补给、径流、排泄条件产生主要的影响。

为简单起见，选择确定的计算模型。根据核桃树沟滑坡的具体工程地质条件，选择主滑方向剖面作为分析剖面，对滑坡进行垂直条分。

3.2 计算参数

根据滑坡的岩土试验结果、参数反演及其与本地区的参数经验值的类比，综合确定该滑坡的稳定性计算参数，如表1。

表1 岩土体抗剪强度指标实验值Table 1 Parameters of rockmass for the stability calculation

在计算中，当条块滑动面位于地下水位以下时，采用饱和状态的强度参数，否则，采用天然状态的强度参数。

考虑参数的变异性，根据Schneider建议的土工参数的变异系数的典型取值范围，取内摩擦角的变异系数为0.1，内聚力的变异系数为0.4，重度的变异系数为0。把抗剪强度参数作为随机变量，重度作为确定变量。根据变异系数、均值和方差的关系，确定基本变量的统计参数，见表2。

3.3 分析计算

稳定性分析选用三峡工程相应规范建议的滑动面为折线形的堆积层滑坡稳定性分析方法。直接选取稳定性系数F作为状态函数，F除是一般变量外，还是随机变量 X1=Cd，X2=Cs，X3=φd及 X4=φs的函数［6］。

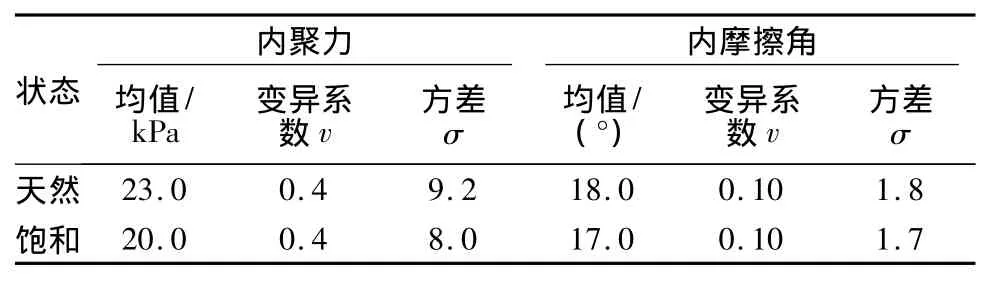
表2 滑坡稳定性计算统计参数值Table 2 Statistical values of basic variables for the stability calculation

考虑随机变量的相关性，并假设内聚力Cd和Cs、内摩擦角φd和φs之间完全相关，且内聚力和内摩擦角之间完全不相关。在分析过程中直接将Cd和Cs，φd和φs捆绑在一起，按相同的规律共同取值，即状态函数只有2个随机变量，即

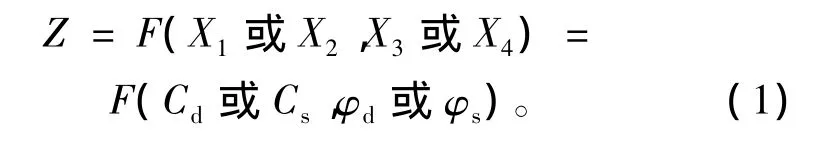
采用函数连分式渐近法，直接变量选择Cd和φd，Cs和 φs作为间接随机变量，则状态函数［7］方程为

变量处理

故

采用函数连分式渐近法求得:

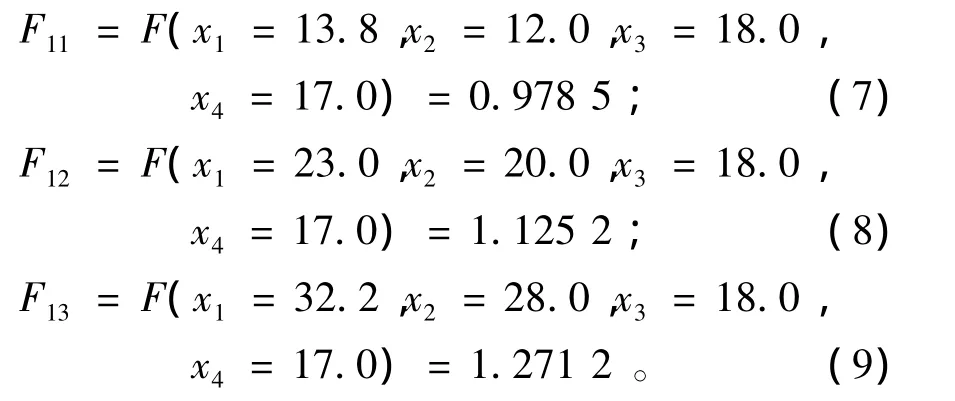
继而求得:

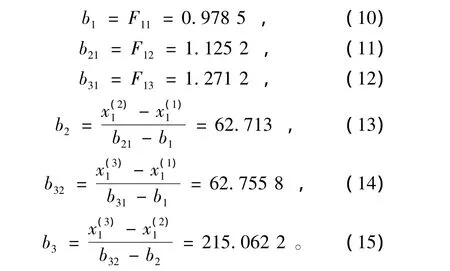
故

求导得

同理对第2个变量求导得

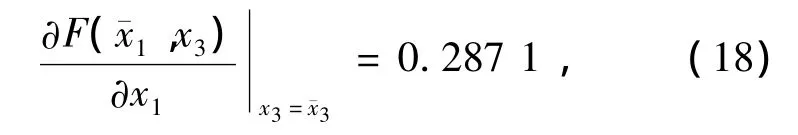
状态函数偏导数为

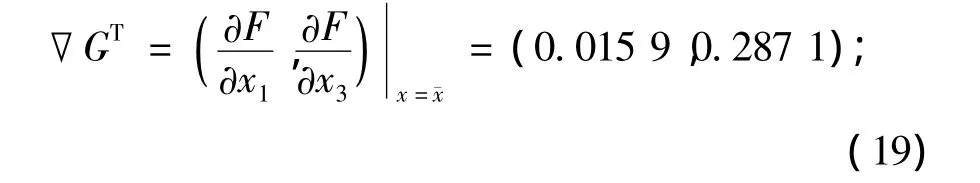
协方差矩阵为

得

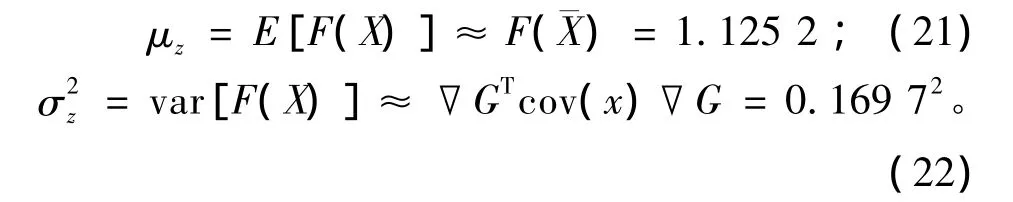
可靠度指标为

破坏概率为

状态函数的变异系数为

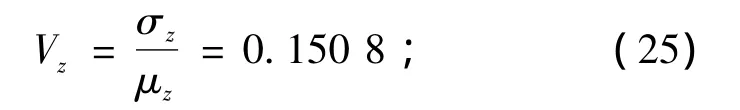
中值稳定安全系数为

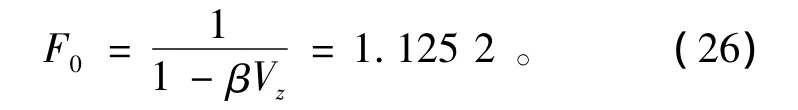
计算结果表明:该滑坡基于中心点法计算的稳定性系数为1.125 2，破坏概率为22.03%;与传统的传递系数定值法计算结果Fs=1.124对比，比较接近。可靠度计算结果为73.77%，符合客观实际。

4 结语

中心点法，利用泰勒级数将非线性状态函数在平均值(亦即中心点 )处展开，并取一次项，在中心点附近取线性近似，使之线性化，计算比较简单。导出解析表达式，考虑了岩土体物理力学参数不确定性的影响，直接给出可靠指标与随机变量统计参数之间的关系。

本文基于中心点法对该滑坡进行可靠度稳定性分析，计算得出的稳定性安全系数大于1，但此滑坡在该计算工况下仍有22.03%的失稳破坏的可能性。结果和传统的定值法结果对比十分接近，能够较好地拟合客观实际工程。

特别适用于状态函数为 F(X1，X2，…，Xn)=R－S的斜坡稳定性分析，这种形式对R，S呈线性状态，这样的状态函数对随机变量的偏导易于计算，从而容易得出状态函数的均值和方差，由此计算出的可靠度指标、破坏概率及中值稳定安全系数，能够较好地拟合工程实际，是未来岸坡稳定性研究发展的主要前沿方向之一，具有重要的研究意义。

［1］唐辉明.工程地质学基础［M］.北京:化学工业出版社，2008.(TANG Hui-ming.Fundamentals of Engineering Geology［M］.Beijing:Chemical Industry Press，2008.(in Chinese))

［2］张倬元.工程地质分析原理［M］.北京:地质出版社，1981.(ZHANG Zhuo-yuan.Principle of Engineering Geology Analysis［M］.Beijing:Geological Press，1981.(in Chinese))

［3］张永兴，胡居义，文海家.滑坡预测预报研究现状述评［J］.地下空间，2003，23(2):200－202.(ZHANG Yong-xing，HU Ju-yi，WEN Hai-jia.Review of the Study on Prediction and Forecast of Landslide［J］.Underground Space，2003，23(2):200 －202.(in Chinese))

［4］晏同珍，杨顺安，方 云.滑坡学［M］.武汉:中国地质大学出版社，2000.(YAN Tong-zhen，YANG Shunan，FANG Yun.Landslide［M］.Wuhan:Press of China University of Geosciences，2000.(in Chinese))

［5］殷坤龙，柳 源.滑坡灾害区划系统研究［J］.中国地质灾害与防治学报，2000，12(4):28－32.(YIN Kun-long，LIU Yuan.Systematic Studies on Landslide Hazard Zonation［J］.The Chinese Journal of Geological Hazard and Control，2000，12(4):28 － 32.(in Chinese))

［6］CHOWDHURY R N.Analysis Methods for Assessing Landslide Risk:Recent Developments［C］∥Proceedings of the 5th International Symposium of Landslide.Rotterdam:Balkema，1988:515－524.

［7］李胡生，熊文林.岩石力学参数概率分布的随机模糊估计方法［J］.固体力学学报，1993，14(4):347－350.(LI Hu-sheng，XIONG Wen-lin.Random Fuzzy Estimation Method for the Probability Distribution of Rock Mechanical Parameters［J］.Acta Mechanica Solida Sinica，1993，14(4):347 －350.(in Chinese))