岩石单轴压缩端部效应的数值仿真分析

麦 戈，唐照平，唐欣薇

(1.仲恺农业工程学院城市建设学院，广州 510225;2.中交第三航务工程勘察设计院有限公司，上海 200032;3.华南理工大学亚热带建筑科学国家重点实验室，广州 510640)

1 研究背景

单轴压缩强度是衡量岩石力学特性的重要指标，通过试验所确定的各种岩石强度要受到试件的尺寸、形状、加载速率、湿度等的影响，例如，由于端部效应的存在，岩石试件在靠近端部会存在复杂的应力分布，引起变形破坏的局部化，从而影响岩石的强度［1］。文献［2］对2种极端垫板情况进行了力学分析，得出端部效应的影响与垫板的刚度性质有关的结论。文献［3］通过大理岩的单轴试验发现，端部加有聚四氟乙烯垫片试验的单轴抗压强度要低于端部未加垫片的。文献［4］利用FLAC3D模拟了因端部摩擦效应而产生的应变局部化。文献［5］通过试验分析指出，若采用特殊的装置减小岩样端部摩擦后，岩石材料强度的尺寸效应就消失了。

虽然许多学者采取许多措施来减少加载端部和岩石试件之间的摩擦力来消除或者减小端部效应，如在试件的两端加特殊垫板(片)，如聚四氟乙烯(PC)垫片、气垫等垫板，仍然不能很好地解决此问题［6－9］。

随着现代数值分析技术和计算机技术的进步，人们开始立足于材料的细观结构，发展数值试验测试技术。区别于实验室力学试验，数值试验不但可以实现各种复杂边界条件，而且可以满足各种理想的边界条件。这为研究材料破损行为的机理，提供了有力支持。

本文基于连续介质力学的方法，采用非线性损伤本构关系描述材料的力学行为，在此基础上，引入岩石力学性能的Weibull随机概率分布，以表征岩石力学参数的非均质特性与损伤局部化现象，建立了岩石细观力学模型。对岩石试件单轴压缩试件进行了数值试验，对不同摩擦系数下，端部效应对岩石试件单轴压缩强度及破坏模式的影响进行了分析。

2 岩石细观本构模型

2.1 单轴应力－应变关系

本文模型基于连续介质损伤力学框架以描述岩石材料在细观尺度下各离散单元的力学特性。按照Lemaitre应变等价原理，受损材料的本构关系可通过无损材料的名义应力与应变关系表示，即

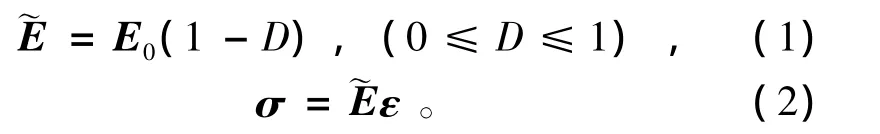
式中:E0为初始弹性模量;为损伤后的弹性模量;D为损伤变量。

2.2 损伤演化定义和强度准则

岩石试件在单轴拉伸时，试件的破裂缝与加载方向垂直且只有一条，即沿最大拉伸变形方向拉断破坏;单向压缩时，试件的破裂呈现平行的多条裂缝，即沿加载方向开裂，这主要由于受压时自由面向外膨胀产生拉伸变形，由此可以认为岩石的受力变形与损伤破裂主要是拉伸变形起控制作用。为简化计算，采用图1所示双折线应力－应变软化本构关系。其中，ft，fm分别为单元材料的初始抗拉强度和拐点M处的残余抗拉强度;εt，εm分别为单元应力达到ft，fm时的主拉应变;εf为材料完全丧失抗拉强度时的极限拉应变。引入fm=λft，(εf－εt)=η(εm－εt)，λ 和 η 分别为单元的残余强度系数和极限应变系数(通常取λ=0.1，η=10)。引入软化段折线模量Et1与Et2以表征上述关系。相应地，式(1)中刚度退化变量D的定义可由式(3)确定。

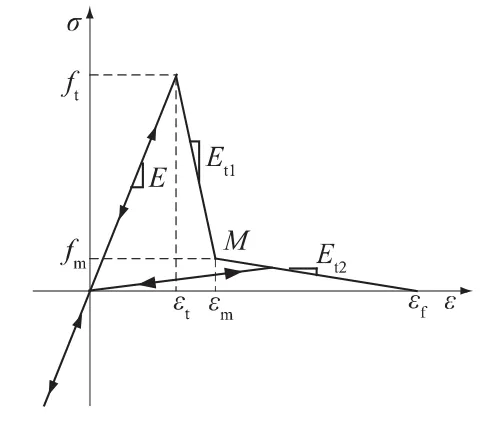
图1 应力－应变本构关系Fig.1 Stress-strain constitutive relation

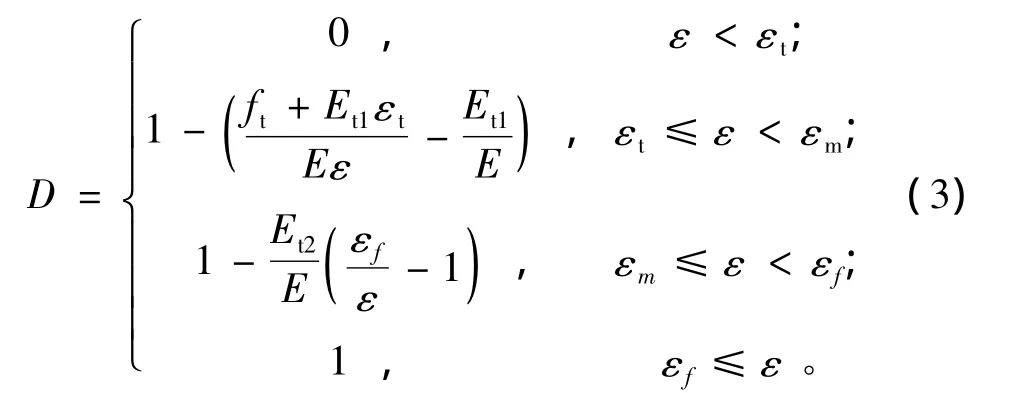
计算模型中采用最大拉应力准则。为满足断裂能守恒准则，定义裂缝扩展单位面积所吸收的能量是唯一的，根据Bazãnt的断裂能守恒原理，基于细观单元的离散尺度以及材料断裂能参数对图1采用的应力应变关系进行调整，以避免计算结果对网格的敏感性。为推广至二维及三维应力状态，本文参考Fenves模型中关于损伤定义由一维扩展至多维的方法，将上述本构模型推广至平面及三维应力状态［10］。

3 单轴压缩的数值试验

3.1 数值模型

数值模型采用二维平面应变有限元模型(如图2)，岩石试样尺寸100 mm×100 mm，划分为100×100个单元，采用位移控制的加载方式。

图2 有限元模型Fig.2 Finite element meshes

考虑到岩石本身存在各种缺陷，如微裂纹、孔洞等，材料力学参数的分布具有一定的随机性。为了更加合理地描述岩石的非均质性，可假定岩石材料细观单元的力学性质(弹性模量、强度)满足Weibull分布，该分布可依照如下分布函数来定义:

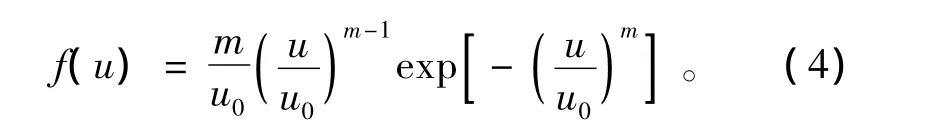
式中:u代表满足该分布参数(如强度、弹性模量等)的数值;m为材料均质度，反映了统计模型中材料结构的均匀程度，当其由小到大变化时，材料细观单元强度分布函数由扁而宽向高而窄变化，细观单元强度趋于均匀;u0是一个与均值E(u)有关的参数。

为了研究端部效应对岩石力学性能的影响，保证结果的可靠性，本文选取6组加载钢板与岩石间的摩擦系数，即 f=0.01，0.2，0.3，0.4，0.5和0.6，基于Monte Carlo法每组产生5个样本，用以反映宏观力学性质相同的岩石的细观结构随机性。随机分布的数值样本如图3所示。颜色灰度反映了单元力学参数的高低。根据衡阳产砂岩的相关试验结果［11］，可选取如下力学性质参数(见表1)。

图3 岩石试件的随机样本Fig.3 Random samples for rock specimens

表1 岩石主要力学参数表Table 1 Mechanical parameters of rock

3.2 结果与分析

图4为不同摩擦系数下岩石试件开裂形态，可见，当加载板与岩石试件摩擦力较小时(f=0.01)，岩石试件的宏观压缩破裂形式主要表现出与加载方向平行的纵向破裂。随着加载板与岩石试件间摩擦系数的增加，岩石试件端部受加载板的侧向约束越强，使得试件的宏观压缩破裂形式表现出X型劈裂或近似斜面剪切破裂。

图4 岩石试件开裂形态Fig.4 Failure patterns of rock specimens

岩石试件的破裂大致分为线性变形—裂纹发展—裂纹贯穿3个阶段。在加载初期，岩石试件受到侧向的约束，在试件两端开始出现局部破坏，并在靠近加载板的一侧形成局部的纵向劈裂裂纹。随着荷载的不断增加，局部裂纹逐渐向试件中间快速发展，直至贯穿整个试样。

图5展示了不同摩擦系数下岩石试件的抗压强度－应变包络曲线。随着端部摩擦系数的增加，岩石试件表现出来的单轴抗压强度趋于增大。这表明试验机压头作用于压垫板压缩试样时，试样的侧向膨胀受到抑制，存在指向试样中心的剪切摩擦力，这有助于提高试样的测试强度。在试样长度较小时尤其显著。

此外，在各组端部摩擦包络曲线下，岩石试件弹性段差别较小，进入非线性软化后，则出现较大的差异。随着端部摩擦系数的增加，岩石试件的应力－应变曲线的峰值逐渐提高，软化段也变得平缓一些。

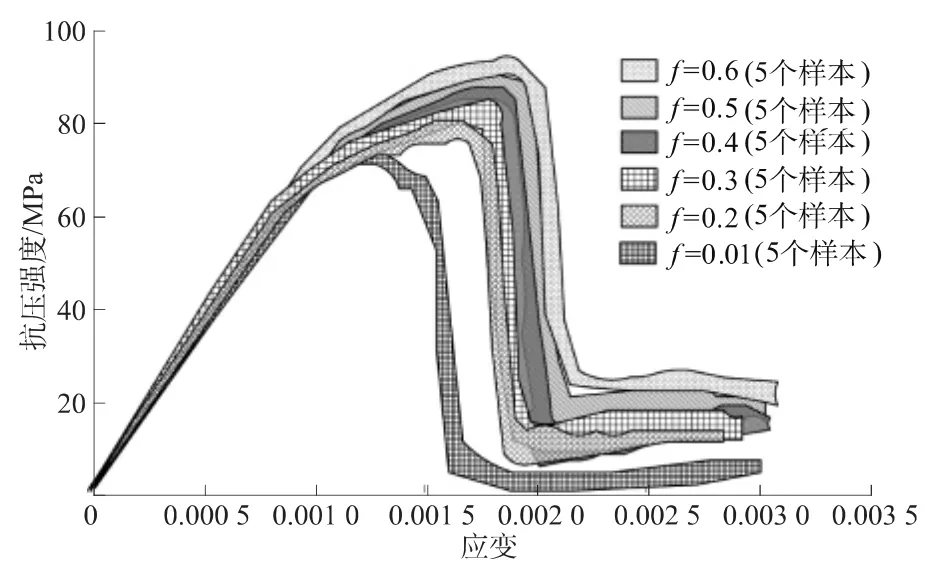
图5 不同摩擦系数的上下包络曲线比较Fig.5 Comparison of upper and lower envelope curves of uniaxial compression of specimens in the presence of different friction indexes

图6给出了不同摩擦系数下，岩石试件抗压强度的变化。可见，随着端部摩擦系数的增加，试件的单轴抗压强度逐渐增加。当摩擦系数达到0.4后，抗压强度增加幅度变小。

图6 不同摩擦系数的抗压强度比较Fig.6 Comparison of compressive strength in the presence of different friction indexes

4 结语

本文基于细观力学，考虑岩石材料的非均质特性，假定岩石材料力学性质符合Weibull概率统计分布，在连续介质损伤力学框架上建立了有限元概率损伤数值模型。基于该模型对岩石单轴压缩强度的端部效应进行了数值仿真试验。结果表明:受端部效应的影响，岩石试件(特别是长度较小)的破裂形态、强度－应变曲线出现显著的影响。为获取真实的岩石力学特性，需有效地控制实验室试验条件，降低端部效应对测量结果的影响。

［1］TANG C A.THAM L G，LEE PK K，et al.Numerical Studies of the Influence of Microstructure on Rock Failure in Uniaxial Compression PartⅡ:Constraint，Slenderness and Size Effect［J］.International Journal of Rock Mechanics and Mining Sciences，2000，37(4):571 －583.

［2］TANG C A，LIU H，LEE P K K，et al.Numerical Studies of the Influence of Microstructure on Rock Failure in Uniaxial Compression Part I:Effect of Heterogeneity［J］.International Journal of Rock Mechanics and Mining Sciences，2000，37(4):555 －569.

［3］尤庆明，苏承东.大理岩试样的长度对单轴压缩试验的影响［J］.岩石力学与工程学报，2004，23(22):2754－2760.(YOU Qing-ming，SU Cheng-dong.Effect of Length of Fine and Coarse Crystal Marble Specimens on Uniaxial Compression Tests［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(22):2754 －2760.(in Chinese))

［4］刘继国.端部摩擦对应变局部化影响的数值模拟［J］.土工基础，2006，20(5):47－60.(LIU Ji-guo.The Simulation to the Effects on Strain Localization Due to End Friction［J］.Soil Engineering and Foundation，2006，20(5):47－60.(in Chinese))

［5］杨圣奇，苏承东，徐卫亚.岩石材料尺寸效应的试验和理论研究［J］.工程力学，2005，22(4):112－118.(YANG Sheng-qi，SU Cheng-dong，XU Wei-ya.Experimental and Theoretical Study of Size Effect of Rock Material［J］.Engineering Mechanics，2005，22(4):112 －118.(in Chinese))

［6］梁正召，唐春安，张娟霞，等.岩石三维破坏数值模型及形状效应的模拟研究［J］.岩土力学，2007，28(4):699 －704.(LIANG Zheng-zhao，TANG Chun-an，ZHANG Juan-xia， et al.Three-dimensional Damage Model for Failure Process of Rocks and Associated Numerical Simulation of Geometry Effect［J］.Rock and Soil Mechanics，2007，28(4):699 －704.(in Chinese))

［7］MOGI K.Dilatancy of Rocks under General Triaxial Stress States with Special Reference to Earthquakes Precursors［J］.Journal of Physics of the Earth，1977，(25):203－217.

［8］MOGI K.Experimental Rock Mechanics［M］.London:Taylor＆ Francis/Balkema，2007.

［9］许东俊.茂木岩石真三轴压缩仪的结果及特点［J］.岩土力学，1980，2(3):77－84.(XU Dong-jun.The Structural and Features of Mogi’s True Triaxial Compression Apparatus for Rock［J］.Rock and Soil Mechanics，1980，2(3):77 －84.(in Chinese))

［10］TANG Xin-wei，ZHOU Yuan-de，ZHANG Chu-han，et al.Study on the Heterogeneity Character of Concrete Failure Based on the Equivalent Probabilistic Model［J］.Journal of Materials in Civil Engineering，ASCE，2011，23(4):402－413.

［11］TANG Xin-wei，ZHANG Chu-han，SHI Jian-jun.A Multiphase Mesostructure Mechanics Approach to the Study of the Fracture-damage Behavior for Concrete［J］.Science China in Series E，2008，51(Sup.2):8－24.