层状非均质各向异性地层中多分量感应测井数值模拟与响应特征

汪建勋

（吉林大学电子科学与技术学院，吉林 长春130012）

0 引 言

多分量感应测井仪器是一种能够同时提供地层纵横向电阻率信息的新一代测井技术［1－3］，该仪器包含有3个相互正交的发射线圈（Tx、Ty和Tz）和接收线圈（Rx、Ry和Rz），利用不同方向发射源在地层中产生出的感应电磁场，同时测量9个不同分量的感应磁场，提取出地层纵横向电阻率、井眼相对倾角等参数。

由于共面线圈系电磁场不再具有轴对称性，需要借助电磁三维数值模拟技术［4－8］进行多分量感应测井响应的研究，其运算效率较低且计算机内存占用量较大。所以，三维数值模拟往往采用较为简单的地层模型，且对电阻率反差较大及层数较多的复杂模型，三维测井响应的准确模拟仍然面临诸多问题。针对感应测井三维数值模拟中存在的问题，研究效率更高和精度更好的其他算法一直受到广泛关注，例如，水平层状和柱状各向异性地层中测井响应的解析算法［9－12］、层状非均质地层中的数值模式匹配算法等均具有精确高效的特点［13－14］，特别是数值模式匹配算法在侧向、感应等常规电测井数值模拟和反演方面已发挥了重要作用［15－19］。此外，数值模式匹配算法同时解决了不含井眼的水平层状地层中多分量感应响应的快速模拟与反演问题，最近已经被成功推广应用与含有井眼和侵入带的水平层状非均质地层中多分量感应测井的数值模拟与反演［20－22］。用数值模式匹配算法进行含有井眼和侵入带的层状非均质地层中多分量感应测井数值模拟的主要困难是柱状电导率界面上的积累面电荷。

本文利用文献［20］至文献［21］中的相关方法，针对柱状分界面上的积累面电荷对电磁场的影响问题，通过傅氏级数展开与分离变量法以及电阻率径向导数的奇异性，建立电磁场水平分量的2个奇异算子方程，用于描述柱状分界面上积累面电荷的效应。并利用模式匹配技术给出层状非均质各向异性地层中磁场并矢Green函数的半解析解以及多分量感应测井响应的计算方法，最后通过数值模拟结果考察不同井眼泥浆电阻率和侵入深度上多分量感应测井响应。

1 理 论

图1是水平层状各向异性非均质地层模型的示意图。模型中的地层总层数假定为N；σHT，n、σVT，n（σHx，n和σVx，n）、（n＝1，2，…，N）分别表示地层n中的原状地层（侵入带）横向和纵向电导率；rxo，n（n＝1，2，…，N）、dn（n＝2，3，…，N）分别是侵入半径和水平界面位置；井眼半径和井眼泥浆电导率分别为a、σmd。图1中还建立了相应坐标系xyz，其中z轴与井轴重合且垂直于地层层面，正交发射和接收线圈分别用（êx，êy，êz）、（Rx，Ry和Rz）表示，它们构成一个简单的多分量感应测井仪器。此外，从图1可以看出地层中的纵横向电导率的空间分布是分片常数的且具有轴对称性，同时电导率函数在柱状界面上出现间断。

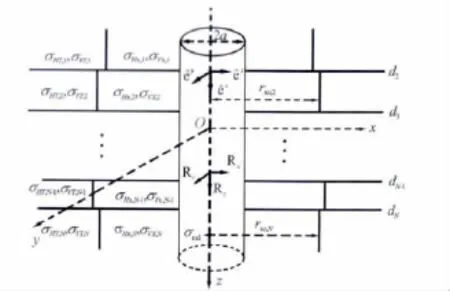
图1 地层模型与阵列多分量感应仪器结构示意图

1.1 Fourier级数展开与奇异算子方程

多分量感应测井响应的数值模拟实质上是求解Maxwell方程［13－14］

式中，Ep、Hp是发射线圈（p＝x，y，z）产生的电磁场＝dian（σH，σH，σV）是电导率张量；磁导率μ为常数；ρs假定为发射线圈的半径；ω为发射信号的角频率，且忽略位移电流影响。利用直角坐标与柱坐标间的转化关系ρ＝和θ＝arctan（x／y），柱坐标系（ρ，θ，z）下，式（1）中的3个正交发射线圈可分别展开为如下形式傅氏级数

其中，l＝0。

由于电导率空间分布的轴对称性的，式（1）中的电磁场水平分量＝（σH，）T和＝（，）T也具有类似的傅氏级数展开形式［20－21］

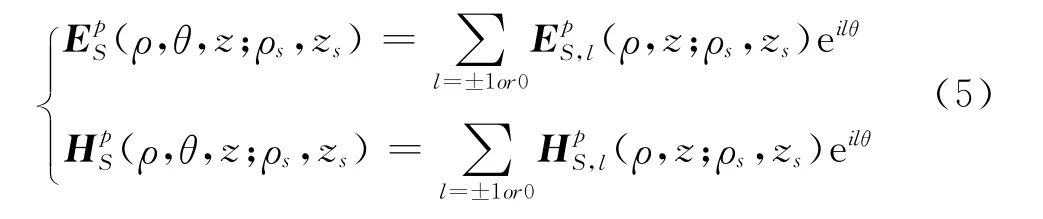
式中，

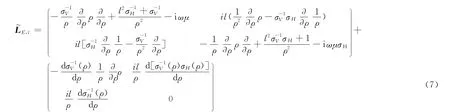
，l是2×2阶微分算子。由于导电率的导数在径向边界上是奇异的，右端项中的第2算子是奇异算子，用于描述柱状分层界面上积累面电荷影响。

磁场水平分量与电场水平分量间的关系方程为

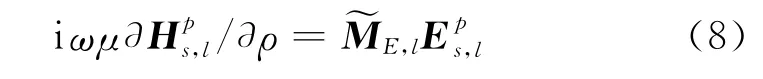
式中，

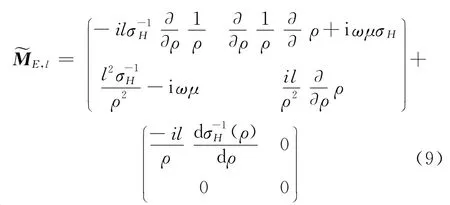
是2×2阶的微分算子且右端的第2算子也是奇异算子。

此外，磁场垂直分量与间的关系方程为

式（6）至式（10）中的各个变量均与极角θ无关，因此，式（1）中电磁场的三维数值模拟问题通过傅氏展开被转化为3个轴对称问题，简化了数值模拟过程，有效提高了模拟效率，特别是式（7）和式（9）中奇异算子的引入，有效描述了积累面电荷对电磁场的影响。

1.2 水平层状非均质地层中的电磁场

利用数值模式匹配算法并经过一系列复杂推导，第n个非均质地层中的电场水平分量可表示为半解析形式［20－21］

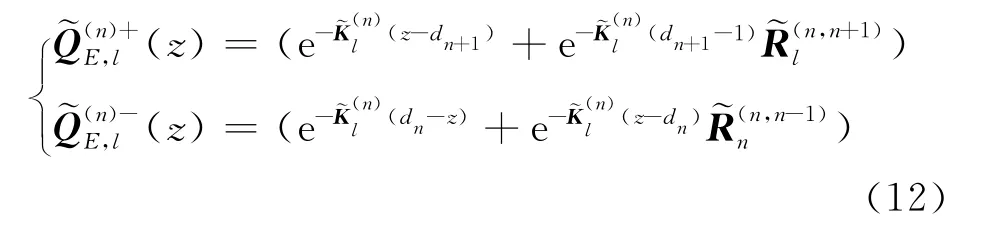
式（12）中的是模式匹配算法中第n个地层上的本征值组成的对角矩阵。进一步将式（11）代入式（8）和（10）中，经整理，得第n个地层中的磁场强度水平分量和垂直分量为

最后，利用柱坐标到直角坐标系的转化关系，将式（15）得到的3个正交磁偶极子磁场转换到直角坐标系中，得磁场张量为

对于给定的测量位置，利用磁场张量的3个主分量Hxx、Hyy和Hzz，可计算出多分量感应测井仪器的3个主响应［1，7］，为

式中，L是发射线圈和接收线圈间的距离。

2 数值模拟结果

首先利用完全柱状各向异性地层中解析法（AM）［10］与本文中的数值模式匹配算法（NMM）得到的数值结果的对比，检验数值模式匹配算法（NMM）的有效性；然后，进一步考察泥浆电阻率和侵入半径变化对多分量感应测井响应的影响。数值模拟中，多分量感应测井仪器的源距假定为0.8m，发射线圈的工作频率为20kHz，井眼半径假定为a＝0.1m。由于垂直井眼中的2个共面线圈系主分量相等即＝，且所有交叉分量等于0，所以这里仅给出2个主分量和的数值结果。

图2是完全柱状各向异性地层中，分别由数值模式匹配（NMM）和解析法（AM）得到的主分量和的对比结果，模型中原状地层纵横向电阻率RV和RH分别是90Ω·m和20Ω·m。图2（a）和图2（b）分别对应于泥浆电阻率为Rmud＝1Ω·m和Rmud＝1 000Ω·m情况下的结果，其中，实线和虚线是由解析法得到的，分散的三角形和五角星是数值模式匹配法的计算结果。结果清楚显示，在收发距为0.1～20m的变化范围内NMM算法和AM所得的数值结果吻合得非常好，说明在大反差电阻率地层以及在大收发距变化范围内，NMM仍然能够得到满意的计算效果。此外，结果也清楚反映出在收发距较小的情况下，泥浆电阻率变化对多分量感应响应的影响往往很大。

为考察层状非均质地层中泥浆电阻率和侵入深度不同时多分量感应测井的响应特征，本文设计出一个9层非均质模型。该模型包含4个高电阻率层和3个低电阻率层以及上下围岩，且所有地层具有各向异性。高电阻率层和低电阻率层厚度均是3m，4个高电阻率层的侵入带和原状地层电阻率相同且分别是（Rhx，Rvx）＝（8，26）Ω·m 和（Rht，Rvt）＝（15，65）Ω·m，从上到下4个高电阻率地层的侵入半径分别是0.1、0.3、0.5m和0.7m。低电阻率层与上下围岩电阻率相等，其值为（Rht，Rvt）＝（2，5）Ω·m且没有侵入。图3是该模型在低电阻率泥浆和高电阻率泥浆2种不同情况下的由NNM算法得到的模拟结果，其中，粗实线和粗虚线分别代表Rmud＝1Ω·m和Rmud＝1 000Ω·m情况下的测井响应。结果显示，泥浆电阻率对视电导率的影响非常明显，且高电阻率泥浆情况下的视电导率与地层电导率更接近。仔细对比不同侵入深度地层上的视电导率的大小，可以看出最上面的无侵高电阻率地层上的视电导率与下面各个有侵高电阻率层上的视电导率存在明显差异，说明侵入对视电导率有明显影响，但其他不同侵入深度的高电阻率地层上视电导率的值相差较小，说明共面线圈系视电导率的探测深度不大。此外，共轴线圈系的响应与常规测井响应相同，高电阻率泥浆上的视电导率小于低电阻率泥浆上的视电导率值，且在不同侵入深度的地层上，视电导率均存在一定差异，说明共轴线圈系比共面线圈系具有更大的探测深度。

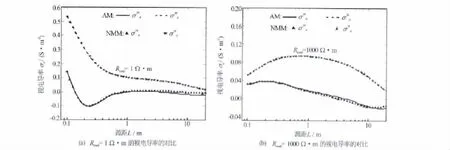
图2 完全柱状各向异性地层中NMM与AM所得数值结果的对比

图3 9层水平层状非均质各向异性地层上不同井眼泥浆和侵入深度情况下多分量感应测井响应

3 结 论

（1）针对柱状分界面上积累面电荷对共轴线圈系电磁响应的影响问题，通过傅氏级数展开与分离变量法以及电阻率径向导数的奇异性，给出关于电磁场水平分量的2个奇异算子方程。

（2）利用模式匹配技术得到了层状非均质各向异性地层中磁场并矢Green函数的半解析表达式，能够进行层状非均质各向异性地层中多分量感应测井响应的数值模拟。

（3）数值计算结果显示，共面线圈系与共轴线圈系的测井响应和存在着较大差异，高电阻率泥浆上视电导率大于低电阻率泥浆上的值，且高电阻率泥浆情况下的视电导率与地层电导率更接近，因此，高电阻率泥浆更有利于共面线圈系资料的解释。

（4）多分量感应响应中另一个现象是视电导率在水平界面附近出现明显犄角以及负的响应，这是由于水平界面上的积累面电荷产生的。此外，多分量感应测井的响应的复杂性给电测井资料处理和解释带来了一个全新的研究课题。

［1］ Zhdanov S，Kennedy D，Peksen E.Foundations of Tensor Induction Well－logging ［J］.Petrophysics，2001，42（6）：588－610.

［2］ 张国艳，肖加奇，郝永杰.三维感应测井数值计算与理论分析 ［J］.测井技术，2012，36（1）：15－19.

［3］ 陈章龙，陈涛，白彦，等.三维感应视电导率推导与地层参数分析 ［J］.测井技术，2011，35（6）：523－527.

［4］ 孙向阳，聂在平，赵延文，等.用矢量有限元方法模拟随钻测井仪在倾斜各向异性地层中的电磁响应［J］.地球物理学报，2008，51（5）：1600－1607.

［5］ 陈桂波，汪宏年，姚敬金，等.用积分方程法模拟各向异性地层中三维电性异常体的电磁响应 ［J］.地球物理学报，2009，52（8）：2174－2181

［6］ 杨守文，汪宏年，陈桂波，等.倾斜各向异性地层中多分量高频电磁波测井响应的三维时域有限差分（FDTD）算法 ［J］.地球物理学报，2009，52（3）：833－841.

［7］ 张烨，汪宏年，陶宏根，等.用电场矢势和标势三维有限体积法算法研究层状各向异性非均质地层中三分量感应测井响应 ［J］.地球物理学报，2012，55（6）：2141－2152.

［8］ 高杰，刘传奇，万金彬.裂缝性储层双侧向测井响应临界角影响因素分析 ［J］.测井技术，2012，36（5）：456－459.

［9］ 姚东华，汪宏年，杨守文，等.用传播矩阵法研究层状正交各向异性地层中三分量感应测井响应 ［J］.地球物理学报，2010，53（12）：3026－3037.

［10］ Wang Hongnian，So P，Yang S W，et al.Numerical Modeling of Multicomponent Induction Well Logging Tools in the Cylindrically Stratified Anisotropic Media［J］.IEEE Trans.On Geosci.and Remote Sensings，2008，46（4）：1134－1146.

［11］ 杨震，刘庆成，岳步江，等.随钻电磁波电阻率测井仪器响应影响因素数值模拟 ［J］.测井技术，2011，35（4）：325－330.

［12］ 张甜甜，唐章宏，李安宗，等.随钻感应电阻率测井响应影响因素分析 ［J］.测井技术，2013，37（3）：239－243.

［13］ 汪宏年，陶宏根，姚敬金，等.用模式匹配算法研究层状各向异性倾斜地层中多分量感应测井响应 ［J］.地球物理学报，2008，51（5）：1591－1599.

［14］ Wang H N，Tao H G，Yao J J，et al.Fast Multiparameter Reconstruction of Multicomponent Induction Well－Logging Datum in a Deviated Well in a Horizontally Stratified Anisotropic Formation ［J］.IEEE Trans.On Geosci.and Remote Sensing，2008，46（5）：1525－1534.

［15］ 汪宏年，杨善德，王艳.各向异性地层中电阻率测井的响应特征 ［J］.石油地球物理勘探，1999，34（6）：649－656.

［16］ Wang H N，Yang S D.Fast Modeling of Micro－spherically Focused Log in a Horizontally Layered Formation［J］.IEEE Trans on Geosci and Remote Sensing，2001，39（10）：2275－2282.

［17］ 姚东华，汪宏年，陶宏根，等.水平层状介质中双侧向测井资料的迭代Tikhonov正则化反演 ［J］.地球物理学报，2012，53（10）：2227－2236.

［18］ Wang H N，Yang S D.A Multiparameter Iterative Inversion of Dual－laterolog in Horizontally Layered Media and Its Error Analysis［J］.IEEE Trans.Geosci.Remote Sens.，2002，40（2）：482－493.

［19］ Wang H N.Simultaneous Reconstruction of Geometric Parameter and Resistivity Around Borehole in Horizontally Stratified Formations from Multiarray Induction Logging Data［J］.IEEE Trans.on Geosci.and Remote Sensing，2003，41（1）：81－89.

［20］ 汪宏年，胡平，陶宏根，等.水平层状非均质横向同性地层中阵列多分量感应测井响应的快速计算 ［J］.地球物理学报，2012，55（2）：717－726.

［21］ Wang H N，Tao H G，Yao J J，et al.An Efficient and Reliable Simulation of Multicomponent Induction Logging Response in Horizontally Stratified Inhomogeneous TI Formations by Numerical Mode－matching Method［J］.IEEE Trans.Geosci.Remote Sen.，2012，50（9）：3383－3395.

［22］ Wang H N.Adaptive Regularization Iterative Inversion of Array Multicomponent Induction Well Logging Datum in a Horizontally Stratified Inhomogeneous TI Formation［J］.IEEE Trans.Geosci.Remote Sen.，2011，49（11）：4483－4492.