分流式电导含水率计测量区域流场分布与实验比较

杨志刚

（大庆油田有限责任公司测试技术服务分公司，黑龙江 大庆163000）

0 引 言

大庆油田已进入高含水后期，产出井的动态监测电导含水率计已在大庆油田推广和应用。原有仪器应用范围有局限性，仪器在特高含水的情况下测量精度不够。为了提高仪器测量精度，开发了分流法电导含水率计［1］。本文采用FLUENT 6.3对分流法电导含水率计进行模拟，并对分流法含水率计进液口附近流体速度矢量方向、油水分布和测量段内持水率进行分析研究。

1 分流法电导含水率计仪器结构及测量原理

电导含水率计的测量原理是通过测得混相（油水两相）电导率并对连续相（水相）电导率进行校正，最终确定离散相体积分数即持水率［2］。分流法电导含水率计是在原电导含水率计的测量通道内加入一非导电的分流管，通过分流部分水实现提高分辨率的目的。仪器结构见图1。分流管居中位于测量通道内部，在集流伞上、下进液口中间通过分隔器隔开，相互之间不连通。由于水密度大于油密度，导致一部分水从下进液口进入，经分流管流出，剩余油水混合流体经上进液口进入测量段内，从而降低测量段内流体的含水率，拉大了高含水情况下仪器响应之间的距离，增加了高含水的曲线插值计算空间。

图1 分流法电导含水率计示意图

2 模型建立与网格划分

2.1 模型简化与建立

为方便仿真计算，建模时作如下假设：①模型中所涉及的壁面都为光滑壁面；②集流过程为全集流，即集流伞与管壁之间完全封闭；③在建模时省略支持集流伞的伞筋。在这些假设条件基础上，把实体三维简化成二维旋转轴对称数值模拟模型，即把三维的模型简化为旋转轴对称面进行二维仿真。这样不但简化了建模，更重要的是提高了计算效率。

利用FLUENT前处理软件GAMBIT进行网格划分，得到简化模型（见图2），网格划分仪器外部流动空间主要采用边长为1mm的三角网格，仪器内部流动通道主要采用边长为0.5mm的三角网格，此次模拟的网格总数为78 182，下入口为速度入口（半径62mm），油水以不同比例相同速度混合从入口处进入管内流动，上出口为自由流动出口（半径9mm），右边界为对称轴，其余边界设置成为光滑壁面。

2.2 多相流模型选择

分流法电导含水率计的测量环境是油水两相（油水物理属性见表1），因此，要在软件中设置多相流模型。鉴于分流法含水率计是在高含水率情况下应用（主相占比重很大），油在管内以油泡的形式存在，即存在明显的油水交界面，而FLUENT提供的多相流模型中只有VOF模型可以得到明显的交界面，而Mixture模型和Eulerian模型对于流体各相是被处理为互相贯通的混合体进行求解的，无明显的相与相之间的交界面，因此，决定选择VOF模型。VOF模型的动量方程［3］为

式中，ρ＝α2ρ2＋（1－α2）ρ1；μ＝α2μ2＋（1－α2）μ1；α2为第二相容积比。

通过求解整个区域内的单一动量方程，作为结果的速度场是由各相共享的。如式（1）所示，动量方程取决于通过容积比率平均密度ρ和容积比率平均黏度μ的所有相的容积比率。

表1 流动材料属性

2.3 湍流模型

FLUENT提供的可选湍流k－ε模型又分为标准k－ε模型、RNG k－ε模型和带旋流修正的（Realizable）k－ε模型。标准k－ε模型对轴向速度剖面的预测结果较好，但对切向速度的预测则较差；Realizable k－ε模型和RNG k－ε模型都表现出比标准的k－ε模型在强流线弯曲、漩涡和旋转方面有更好的表现，具有更高的可信度和精度。由于流体进入含水率计时出现急流、流线弯曲和径向速度突变等现象，Realizable k－ε模型是1个新模型，在有急流或者流线弯曲的模型中相对于RNG k－ε模型没有明显的优势，因此，选择经典的RNG k－ε模型作为此次模拟的湍流模型，求解算法和求解控制参数等参数都保持默认值，RNG k－ε模型的输运方程［3］为

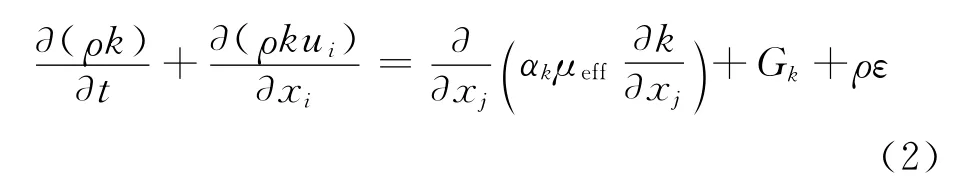
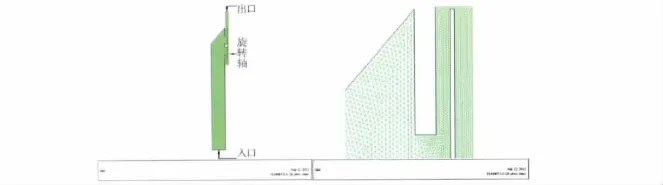
图2 含水率计网格划分模型

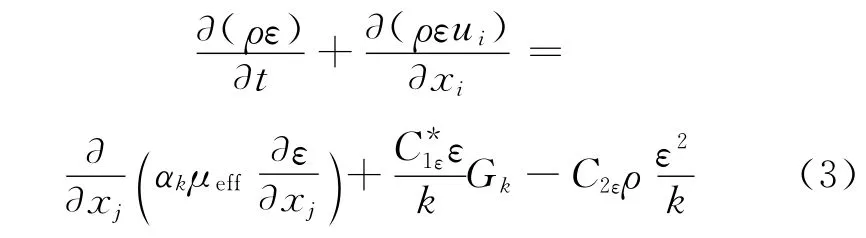
式中，k为湍动能；ε为湍动耗散率；Gk是由层流速度梯度而产生的湍流动能μeff为有效黏度为时均应变率引起的项为时均应变率和αε是湍流Prandtl数，αk＝αε＝1.39；经验常数C1ε＝1.42，C2ε＝1.68，Cμ＝0.0845，η0＝4.377，β＝0.012。

3 仿真结果分析

根据所选择的模型，对分流法电导含水率计进液口附近湍流流体进行数值计算，得到了进液口附近流体速度矢量图和油水分布图，计算了各流量高含水情况下的持水率，并与室内实验结果进行比较。

图3为不同流量含水率90%含水率计进液口附近流体速度矢量图。从图3可以看出，大部分流体速度矢量方向是指向上进液口，但距下进液口较近的流体速度矢量方向是指向下进液口的，说明下进液口具有分流效果。随着流量的增加，流体轴向速度增大，速度矢量中轴向速度分量比重增加，速度矢量方向会向轴向方向偏移，油相由于受到滑脱速度的影响，速度矢量方向偏移会更明显，导致部分油相不会直接进入进液口，反而会沿着集流伞壁聚集到集流器顶端处堆积，最终沿着进液口壁面进入测量区域（见图4）。

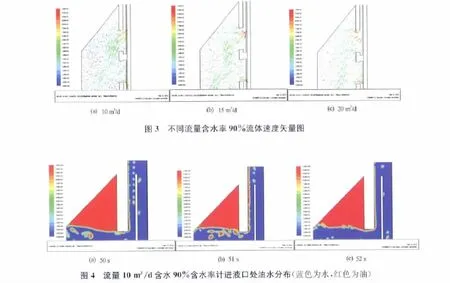
从图4中可以看出，仪器管壁内侧有一层油膜，仪器中心部分主要为水，偶尔含有小油泡。随着时间的变化，油膜会出现间断，油膜厚度也有变化。出现这一现象是由于毛细管压力的存在，聚集在集流器顶端的油必须克服毛细管力才能进入仪器内部流动通道，进而导致聚集在顶端的油会以一股一股的形式沿仪器壁面进入内部流动通道。为避免这种现象影响测量数据的可靠性，必须测量一段时间内的平均值作为测量数据。

由以上分析可知，仪器内部油水两相的流型符合环状流动结构，该流动结构符合由Begovich和Watson在1978年给出的混相（油水两相）电导率σm和主相（水相）电导率σw与连续相体积分数（持水率）Yw的关系前提条件，其关系式［4］为

分流法电导含水率计测量区域输出为电压值，经过放大、滤波、压频转换输出到地面上的为频率值，且全水时的频率值fw、混相时的频率值fm、水相电导率σw和混相电导率值σm，四者存在关系为

联立式（4）、式（5），整理得到频率比与持水率的关系

图5为利用式（6）和室内实验得到的频率比计算出的持水率与利用FLUENT软件模拟相同测量区域内持水率的对比图。图5中，利用FLUENT模拟算出的持水率曲线与室内实验得到的持水率曲线基本一样，都是在流量为10m3／d左右处出现最低值，从10m3／d开始随着流量的增加，持水率也逐渐变大。但对于低流量情况下，与实验值相比模拟值偏低，主要原因在室内实验得到的低流量持水率主要受滑脱效应影响，流量越低滑脱效果越明显，持水率越高，滑脱效应又与界面张力密切相关，VOF模型对于两相界面采用几何重构的思想进行处理，没有准确确定两相界面的物理和几何特性，因此VOF模型对界面张力的处理与真实情况有出入，导致模拟低流量情况下滑脱效应没有充分体现出来，最终导致计算出的持水率偏低。

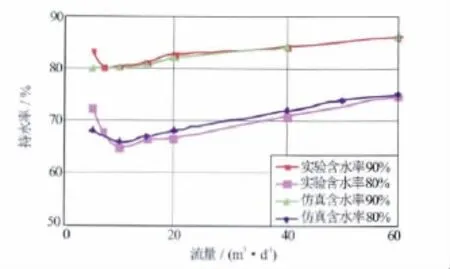
图5 持水率的实验值与仿真结果对比

4 结 论

（1）利用流体力学软件FLUENT成功模拟分流法电导含水率计进液口油水两相流动规律，发现油相通过含水率计上进液口主要是沿进液口壁面流入，并在测量段形成环状流。

（2）通过Begovich和Watson提出的公式得到频率比与持水率之间的关系，利用该关系得到持水率的室内实验值。与仿真结果对比表明，在流量大于10m3／d时仿真结果与室内实验值基本吻合。

（3）在低流量情况下FLUENT软件提供的VOF多相流模型不能准确反映出滑脱现象对油水运动规律的影响。

［1］ 冉磊.基于分流法的高分辨率含水率计现场应用分析［J］.石油仪器，2012，26（1）：51－54.

［2］ 史华蕾，胡金海.一种改进后的阻抗式含水率计现场应用分析与评价 ［J］.国外测井技术，2010（1）：57－59.

［3］ 王福军.计算流体力学分析－CFD软件原理与应用［M］.北京：清华大学出版社，2004：45－47.

［4］ John M Begovich，Watson J S.An Electroconductivity Technique for the Measurement of Axial Variation of Holdups in Three－phase Fluidized Beds ［J］.AIChE Journal，1978，24（2）：351－354.