低维Hom-Leibniz代数分类
2013-12-03徐丽媛王春月张若兰张庆成白城师范学院数学系吉林白城7000吉林工程技术师范学院应用理学院长春005
徐丽媛, 王春月, 张若兰, 张庆成(. 白城师范学院 数学系, 吉林 白城 7000; . 吉林工程技术师范学院 应用理学院, 长春 005;
3. 东北师范大学 数学与统计学院, 长春 130024)
代数形变理论最早由Gerstenhaber[1]提出. Hom-代数是代数形变理论中的一类, 文献[2-4]引入了Hom-代数的概念并进行了系统研究. Makhlouf等[5]把Leibniz代数推广为Hom-Leibniz代数. 文献[6]进一步研究了Hom-Leibniz代数的结构理论. 文献[7-9]研究了Hom-Lie代数、 Hom-Lie超代数和Hom-Lie color代数. 本文利用文献[10]中低维Leibniz代数的分类, 通过待定系数法, 确定了低维Leibniz代数自同态的种类, 从而实现了二维、 三维非李代数的Hom-Leibniz代数分类.
1 二维Hom-Leibniz代数的分类
定义1[2]设L是复数域上的向量空间, [-,-]是L上的二元双线性运算, 线性映射α:L→L满足α([x,y])=[α(x),α(y)], ∀x,y∈L, 则称(L,[-,-],α)是一个Hom-代数.
定义2[10]Leibniz代数L是一个向量空间, 其上定义了一个括积运算: [-,-]:L×L→L, 满足等式: [x,[y,z]]=[[x,y],z]+[y,[x,z]], ∀x,y,z∈L.
由定义1知, 当Leibniz代数满足反交换时是Lie代数.
定义3[5]设(L,[-,-],α)是复数域上的Hom-代数, 如果L满足: [α(x),[y,z]]=[[x,y],α(z)]+[α(y),[x,z]], ∀x,y,z∈L, 则称L是Hom-Leibniz代数.
定理1设(L,[-,-])是一个Leibniz代数,α:L→L是L的自同态,α([x,y])=[α(x),α(y)], ∀x,y∈L. 令[-,-]α=α([x,y]), 则(L,[-,-]α,α)是Hom-Leibniz代数.
证明: 设(L,[-,-])是Leibniz代数,α:L→L的自同态,α([x,y])=[α(x),α(y)]. 令[-,-]α=α([x,y]), ∀x,y∈L, 则根据定义1, (L,[-,-]α)是Hom-代数.
因此, [α(x),[y,z]α]α=[[x,y]α,α(z)]α+[α(y),[x,z]α]α,L是Hom-Leibniz代数.
引理1[10]设(L,[-,-])是Leibniz代数,e1,e2是L的基, 则二维非李代数的Leibniz代数分类为:
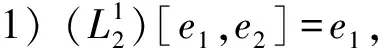


证明: 设L是二维非李代数的Leibniz代数,L的基向量为e1,e2,α:L→L的自同态, 有α(e1)=p1e1+p2e2,α(e2)=q1e1+q2e2. 由引理1和定理1知, 当L是非李代数时, 有:
1)α([e1,e1])=[α(e1),α(e1)]=0,α([e1,e2])=[αe1,αe1]=α(e1)=p1e1+p2e2,α([e2,e2])=[α(e2),α(e2)]=0, 得到方程组p1p2=0,p1q2=p1,p2=0,q1p2=0,q1q2=0. 于是有:
①q2=0,p1=0,p2=0,q1是任意的;
②q2≠0,q1=0,p2=0,p1是任意的.

2 三维Hom-Leibniz代数的分类
引理2[10]设(L,[-,-])是Leibniz代数, 则三维非李代数的Leibniz代数分类有如下13种:
1) [e2,e2]=e3;
2) [e2,e1]=e3;
3) [e1,e1]=e3, [e2,e2]=e3;
4) [e1,e1]=e3, [e2,e1]=ke3, [e2,e2]=e3;
5) [e3,e2]=e3;
6) [e1,e1]=e3, [e1,e2]=e2, [e2,e1]=-e2;
7) [e1,e2]=e2, [e2,e1]=-e2, [e3,e1]=ke3;
8) [e1,e2]=e2, [e2,e1]=-e2, [e2,e2]=e3, [e3,e1]=-2e3;
9) [e1,e2]=e1, [e3,e2]=e3;
10) [e1,e2]=e1, [e2,e2]=e3;
11) [e1,e2]=e1+e3, [e3,e2]=ke3;
12) [e1,e2]=e3, [e2,e2]=e1;
13) [e2,e3]=e1+e2, [e1,e3]=ke2.
其中基向量的其余括积均为0,k≠0.
定理3设(L,[-,-]α)是Hom-Leibniz代数, 则非李代数的三维Hom-Leibniz代数分类有如下19种:
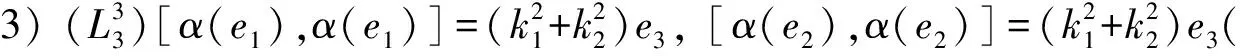

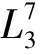

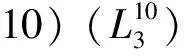




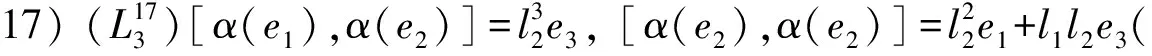
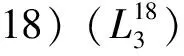

证明: 设L是Leibniz代数, 且dimL=3,α:L→L是L的自同态. 设L的基向量为e1,e2,e3,
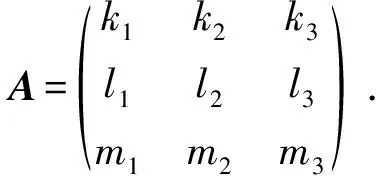
1) [e2,e2]=e3. 根据定理1, 有:α([e1,e1])=α(e3),α([e1,e2])=0,α([e1,e3])=0,α([e2,e1])=0,α([e2,e2])=0,α([e2,e3])=0,α([e3,e1])=0,α([e3,e2])=0,α([e3,e3])=0, 则有
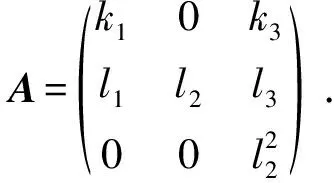
2) [e2,e1]=e3. 从而有:α([e1,e1])=0,α([e1,e2])=0,α([e1,e3])=0,α([e2,e1])=α(e3),α([e2,e2])=0,α([e2,e3])=0. 经过计算得
分析得:
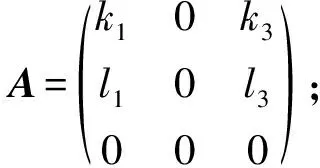
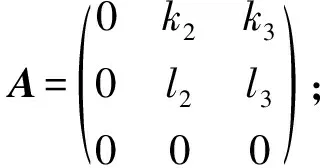

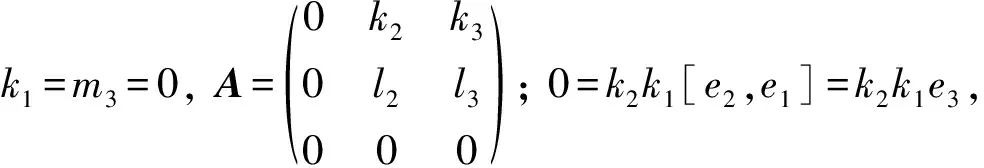
乘法表为[α(e2),α(e1)]=k1l2e3, 其中k1l2≠0.
3)α([e1,e1])=α(e3),α([e1,e2])=0,α([e1,e3])=0,α([e2,e1])=0,α([e2,e2])=α(e3),α([e2,e3])=0,α([e3,e1])=0,α([e3,e2])=0,α([e3,e3])=0. 化简得
分析得:

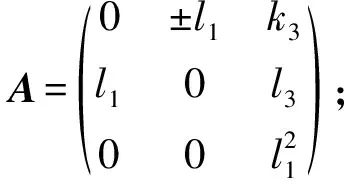

4) [e1,e1]=e3, [e2,e1]=ke3, [e2,e2]=e3. 根据定理1, 有:α([e1,e1])=α(e3),α([e1,e2])=0,α([e1,e3])=0,α([e2,e1])=kα(e3),α([e2,e2])=α(e3),α([e2,e3])=0,α([e3,e1])=0,α([e3,e2])=0,α([e3,e3])=0. 化简得
解得:
5) [e3,e2]=e3. 根据定理1, 有:α([e1,e1])=0,α([e1,e2])=0,α([e1,e3])=0,α([e2,e1])=0,α([e2,e2])=0,α([e2,e3])=0,α([e3,e1])=0,α([e3,e2])=α(e3),α([e3,e3])=0. 化简得
分析得:
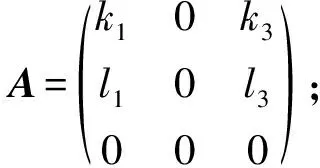

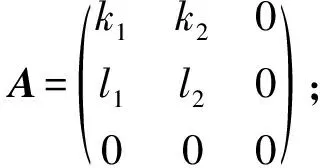
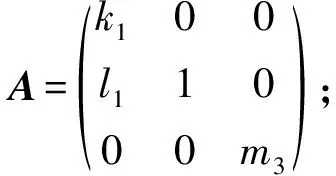

得一种乘法表: [α(e3),α(e2)]=m3e3, 其中m3≠0.
6) [e1,e1]=e3, [e1,e2]=e2, [e2,e1]=-e2. 根据定理1, 化简得
分析得:
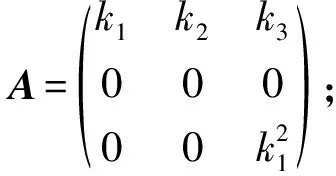

得两种乘法表:
(ii) [α(e1),α(e1)]=e3, [α(e1),α(e2)]=l2e2, [α(e2),α(e1)]=-l2e2, 其中k1l2≠0.
7) [e1,e2]=e2, [e2,e1]=-e2, [e3,e1]=ke3. 根据定理1, 化简得
所以有:
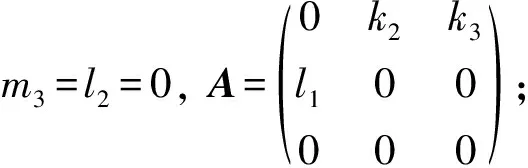
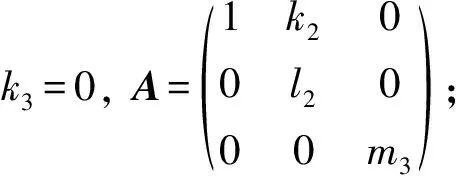

得一种乘法表: [α(e1),α(e2)]=l2e2, [α(e2),α(e1)]=-l2e2, 其中l2≠0.
8) [e1,e2]=e2, [e2,e1]=-e2, [e2,e2]=e3, [e3,e1]=-2e3. 根据定理1, 化简得
分析得:
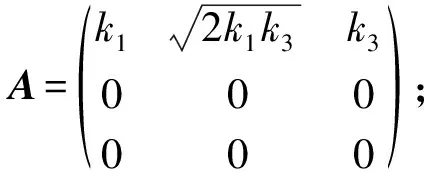
② 当m3=0,k1k3<0时,A不存在;
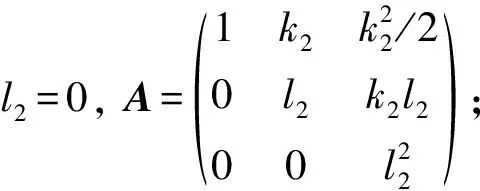
9) [e1,e2]=e1, [e3,e2]=e3. 根据定理1, 化简得
分析得:

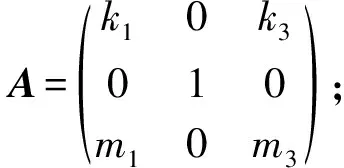

得一种乘法表: [α(e1),α(e2)]=k1e1+k3e3, [α(e3),α(e2)]=m1e1+m3e3, 其中k1+k3+m1+m3≠0.
10) [e1,e2]=e1, [e2,e2]=e3. 根据定理1, 化简得
分析得:

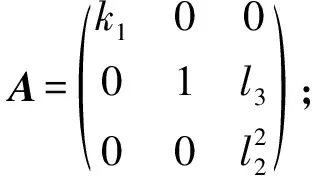

得两种乘法表:
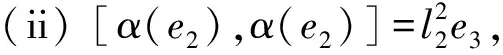
11) [e1,e2]=e1+e3, [e3,e2]=ke3. 根据定理1, 化简得
分析得:
①l2≠0,l1=l3=0,m1≠0,l2=k,m3=kk1+k2k3-k3,k≠1,m1=(1-k)(kk1+k2k3-k3),

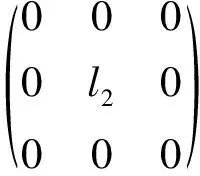


得4种乘法表:
(i) [α(e1),α(e2)]=k1e1+e2+k3e3, [α(e3),α(e2)]=k(1-l2)k1e1+k1e3;
(ii) [α(e1),α(e2)]=k1e1-e2+k3e3, [α(e3),α(e2)]=k(k-1)k1e1-kk1e3;
(iii) [α(e1),α(e2)]=(1-k)k3e1+ke2+k3e3, [α(e3),α(e2)]=-k(k-1)2k3e1+k(k-1)e3;
(iv) [α(e1),α(e2)]=k1e1+e2+k3e3, [α(e3),α(e2)]=k(k1-k3+kk3)e3.
12) [e1,e2]=e3, [e2,e2]=e1. 根据定理1, 化简得

13) [e2,e3]=e1+e2, [e1,e3]=ke2. 根据定理1, 化简得
分析得:
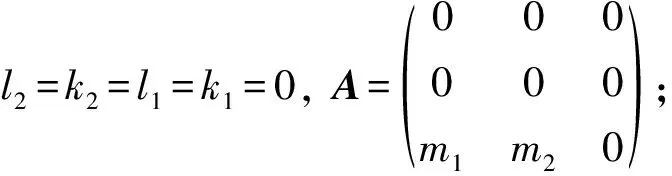
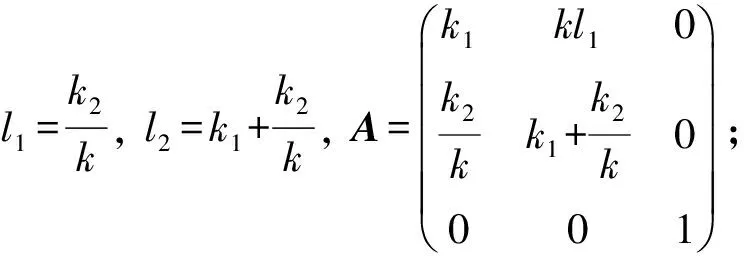

得两种乘法表:
(i) [α(e2),α(e3)]=(k1+l1)e1+(kl1+k1+l1)e2, [α(e1),α(e3)]=kl1e1+k(k1+l1)e2;
(ii) [α(e2),α(e3)]=(k1+l1)e1+k(kl1m3+k1+l1)e2, [α(e1),α(e3)]=kl1e1+k(k1m3+l1)e2.
证毕.
[1] Gerstenhaber M. On the Deformation of Rings and Algebres [J]. The Ann of Math, 1964, 79(1): 59-103.
[2] Larsson D, Silrestrov S D. Quasi-Hom-Lie Algebras, Central Extensions and 2-Cocycle-Like Indentities [J]. J of Algebra, 2005, 288(2): 321-344.
[3] Makhlouf A, Silvestrov S P. Hom-Lie Admissible Hom-Coalgebras and Hom-Hopf Algebras [J/OL]. 2007-11-01. http: //arxiv.org/pdf/0709.2413.pdf.
[4] Hartwig J T, Larsson D, Silvestrov S D. Derformations of Lie Algebras Usingσ-Derivations [J]. J of Algebra, 2006, 295(2): 314-361.
[5] Makhlouf A, Silvestrov S D. Notes on Formal Deformations of Hom-Associative and Hom-Lie Algebras [J/OL]. 2007-12-19. http://arxiv.org/abs/0712.3130.
[6] Ammar F, Ayadi I, Mabrouk S, et al. Quadratic Color Hom-Lie Algebras [J/OL]. 2012-04-23. http://arxiv.org/pdf.1204.5155.pdf.
[7] Ammar F, Makhlouf A. Hom-Lie Superalgebras and Hom-Lie Admissible Superalgebras [J]. J of Algebra, 2010, 324(7): 1513-1528.
[8] Ammar F, Makhlouf A, Saadoui N. Cohomology of Hom-Lie Superalgebras andq-Deformed Witt Superalgebra [J/OL]. 2012-04-27. http://arxiv.org/pdf/1204.6244.pdf.
[9] YUAN La-mei. Hom-Lie Color Algebra Structures [J]. Commu in Algebra, 2012, 40(2): 575-592.
[10] JIANG Qi-fen. Classification of 3-Dimensional Leibniz Algebras [J]. Journal of Mathematical Research and Exposition, 2007, 27(4): 677-686. (蒋启芬. 三维Leibniz代数的分类 [J]. 数学研究与评论, 2007, 27(4): 677-686.)
