硼化氮-石墨烯杂化单原子层电学性质的第一原理

安丽娟,庞志远

(天津科技大学 理学院,天津 300457)

自从在实验上发现石墨烯后,因其独特的性质已引起人们广泛关注[1],如无质量的Dirac费米子和奇异的量子Hall效应等[2-7].由于石墨烯具有正六边形蜂窝状结构,因此也激发了人们对与其具有相同晶体结构体系材料[8-9]的研究.与石墨烯的零带隙半导体不同,单层硼化氮片(h-BN)为宽带系的绝缘体,其带隙为5.9 eV[8].由于h-BN与石墨烯具有相似的晶格参数,因此可将h-BN与石墨烯杂化形成异质结构,通过控制嵌入体h-BN的尺寸调制其带隙.文献[10-11]在该体系中还观察到了金属到绝缘体的转变.石墨烯有2个相同的子格子,若子格子的数目不同(失配),则会产生带间态[12].

本文分别将三角形h-BN嵌入石墨烯中和三角形石墨烯片嵌入二维h-BN中,研究该杂化体系的电子结构随三角形嵌入体尺寸的变化规律.

1 计算方法

采用密度泛函理论进行自洽计算[13],应用广义梯度近似方法处理电子间的交换关联作用,具体形式为Perdew-Burke-Emzerhof格式[14],基函数为极化泛函的双数值基组.几何优化弛豫时的能量收敛标准为2.7×10-4eV,自洽场的电荷密度收敛标准为2.7×10-5eV,Brillouin区K点选为10×10×1.

2 结果与讨论

采用的模拟结构为六方超胞,如图1(A)所示,其中灰、蓝和粉色球分别代表C,N和B原子.超胞的晶格常数为OA=OB=8a,其中a=0.246 nm为纯石墨烯的晶格常数；为消除周期性影像的影响,OC为1 nm的真空层,在超胞内有128个原子,该杂化结构用BxNy/C128-x-y表示.由于石墨烯与h-BN具有相似的晶格常数,因此超胞空间不变,只允许原子坐标弛豫.

BxNy/C128-x-y中的石墨烯与h-BN在界面处有两种可能情况:

1) B与C相连,如图1(B)所示,此时石墨烯的子格子失配数为x-y；

2) N与C相连,如图1(C)所示,此时石墨烯的子格子失配数为y-x.

下面先讨论边界为C—B键的情形.h-BN片尺寸逐渐增大的BxNy/C128-x-y结构分别为B7N6/C115,B12N10/C106,B18N15/C95,B25N21/C82,B33N28/C67,B36N31/C61,B43N39/C46,B49N46/C33,B54N52/C22和B58N57/C13.可见石墨烯的子格子失配数先逐渐增大(1→5)后再逐渐减小(5→1),B33N28/C67和B36N31/C61为从纯石墨烯过渡到纯二维h-BN的临界点,其石墨烯的子格子失配数均为5,越过该临界结构即可认为三角形石墨烯已嵌入二维h-BN中.将BxNy/C128-x-y中的超胞扩大2×2倍后如图1(D)所示,其中“*”表示临界结构.由图1(D)可见,在临界结构前h-BN嵌入石墨烯中,在临界结构后石墨烯嵌入二维h-BN中.

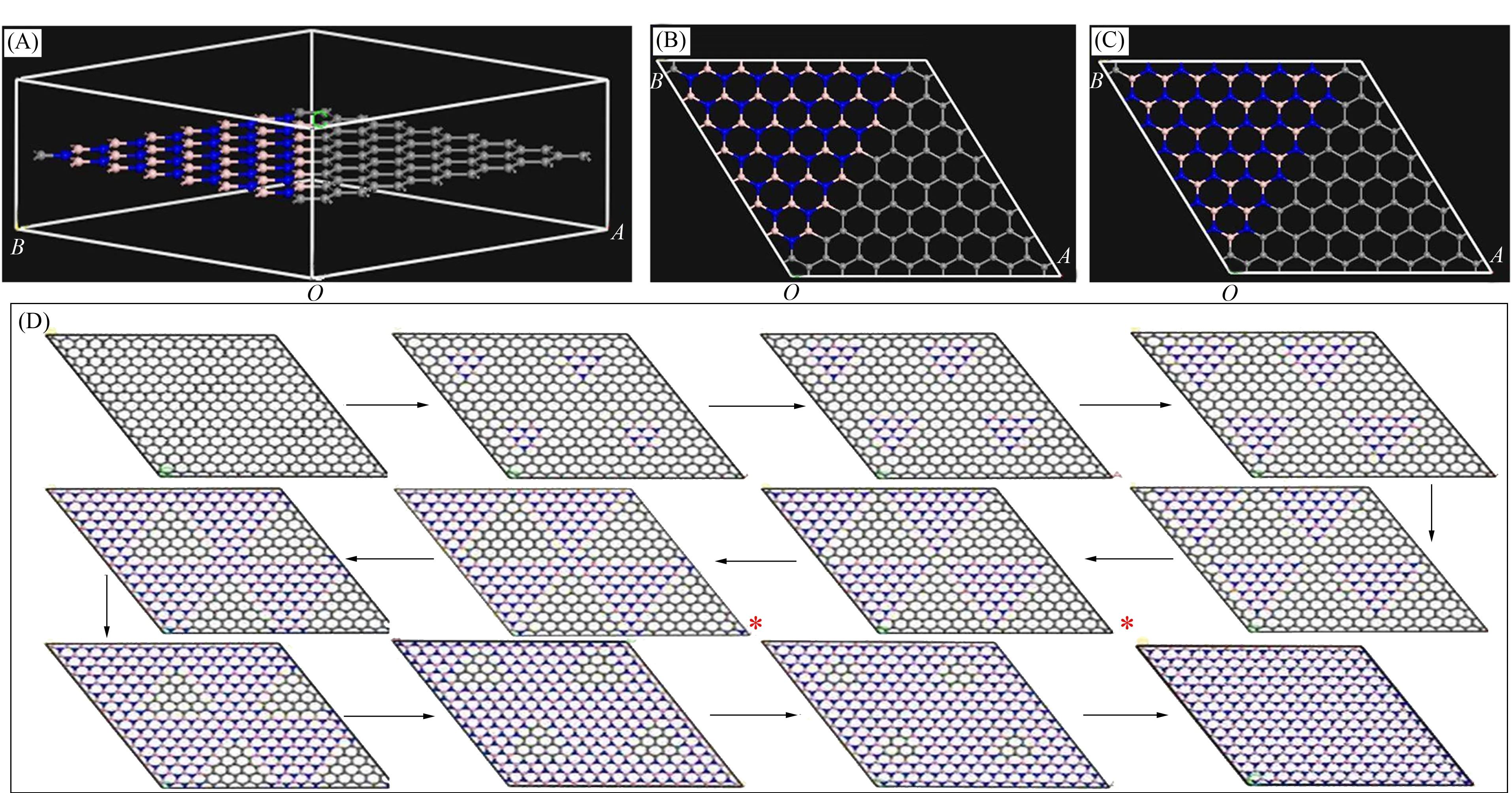
图1 BxNy/C128-x-y的结构模型Fig.1 Structural model of the BxNy/C128-x-y

BxNy/C128-x-y的电子能带结构如图2所示.由图2可见:纯净的石墨烯为零带隙半导体,在K点色散为线性关系,因此电荷载流子为Dirac费米子;纯净的二维h-BN带隙约为5 eV,由于密度泛函关于带隙的理论计算值小于实验值,因此h-BN为绝缘体；在所有杂化结构中均出现带间态,这是由于h-BN与石墨烯杂化使石墨烯子格子失配所致,带间态的个数与石墨烯子格子失配数一致；带间态的形态与结构杂化的方式有关.带间态在临界结构前相对色散,如图2(A)～(F)所示；带间态在临界结构后相对平直,如图2(G)～(L)所示,表明带间态的空间分布在临界结构前相对分散,在临界结构后则相对局域;在临界结构前,当失配数为偶数时(B12N10/C106,B25N21/C82),带间态在费米能处交汇为金属性,当失配数为奇数时(B7N6/C115,B18N15/C95,B33N28/C67),则为窄带隙间接半导体性,表明能带结构可根据杂化结构控制.

图2 BxNy/C128-x-y的能带结构Fig.2 Electronic band structures of the BxNy/C128-x-y

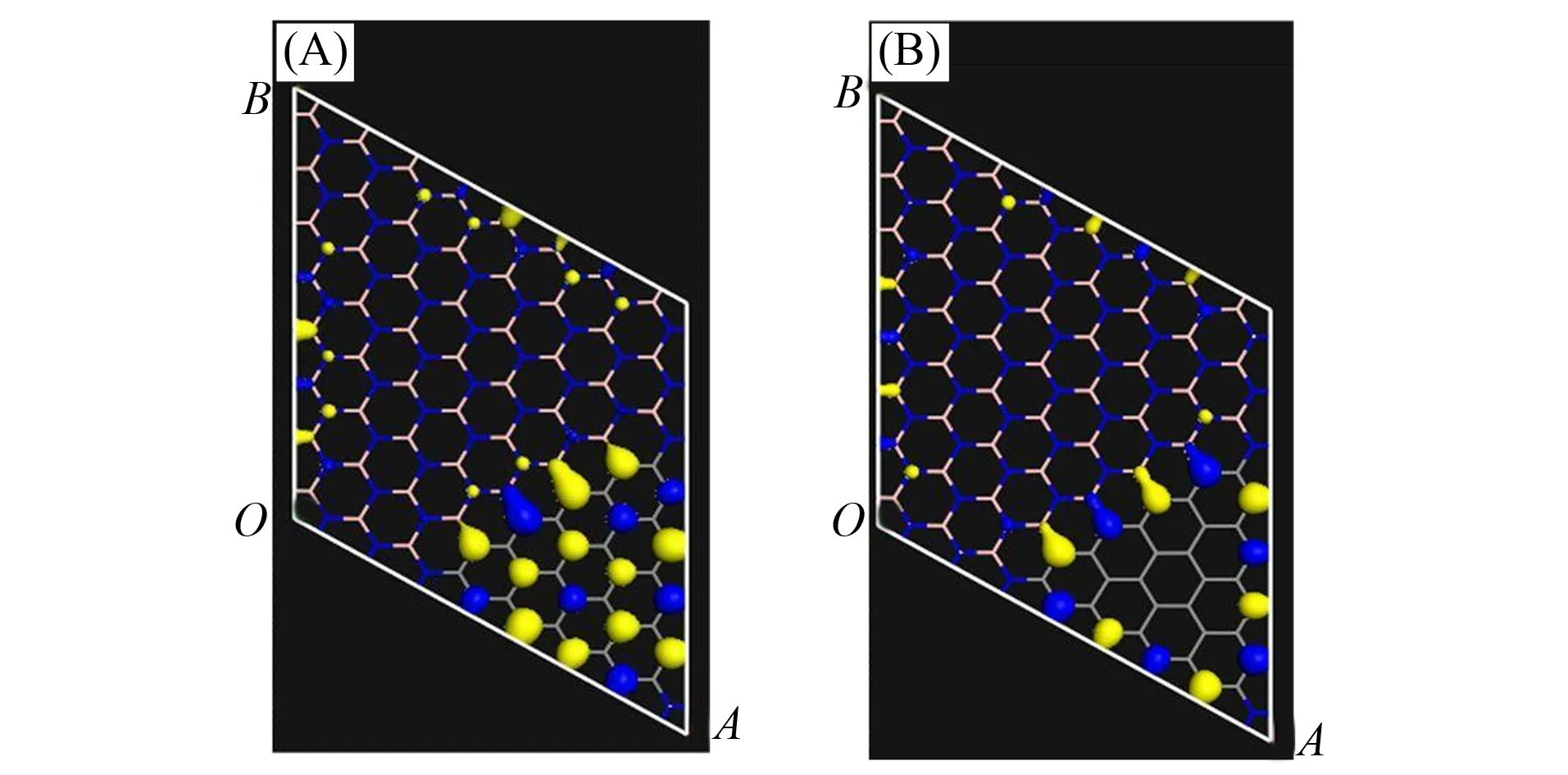
图3 杂化结构B49N46/C33带间态的空间分布Fig.3 Distribution of midgap states for B49N46/C33

在临界结构后,三角形石墨烯片被限域在绝缘的二维h-BN中,与三角形石墨烯片结构[12]类似.因此在该杂化结构中,带间态主要以非键态分布在三角形石墨烯的某个子格子上,如图3所示,其中(A)为扩展态,(B)为边界态.由图3可见,由于空间限制及成键电子的边界陷阱和π电子的极化效应[12,15],因此带间态均表现出较强的电子态,即这些态在能带结构中是平直的,且易于发生自旋劈裂而呈磁性,如图2(G)～(L)所示.

当BxNy/C128-x-y中石墨烯与h-BN的界面处为C—N键时,结果与C—B键的情况相似.当界面处为C—B键时,该体系类似p型掺杂,带间态位于带隙的偏下方；当界面处为C—N键时,体系类似n型掺杂,带间态位于带隙的偏上方.由于B为强Lewis酸原子,在杂化结构界面处的C和B间可驱使更多的电子转移,即C—B键比C—N键强,因此当两个不同的体系(石墨烯和h-BN杂化)用C—B键相连比C—N键相连更稳定[16].

综上所述,两个具有相似晶格参数的石墨烯和h-BN体系可互相嵌入形成杂化结构,利用控制嵌入体尺寸的方式可调制能带结构.

[1] Novoselov K S,Geim A K,Morozov S V,et al.Electric Field Effect in Atomically Thin Carbon Films [J].Science,2004,306：666-669.

[2] Novoselov K S,Geim A K,Morozov S V,et al.Two-Dimensional Gas of Massless Dirac Fermions in Graphene [J].Nature,2005,438:197-200.

[3] ZHANG Yuan-bo,TAN Yan-wen,Stormer H L,et al.Experimental Observation of the Quantum Hall Effect and Berry’s Phase in Graphene [J].Nature,2005,438:201-204.

[4] Meyer J C,Geim A K,Katsnelson M I,et al.The Structure of Suspended Graphene Sheets [J].Nature,2007,446:60-63.

[5] Geim A K,Novoselov K S.The Rise of Graphene [J].Nat Mater,2007,6:183-191.

[6] Katsnelson M I.Graphene:Carbon in Two Dimensions [J].Materstoday,2007,10(1/2):20-27.

[7] Novoselov K S,Jiang Z,Zhang Y,et al.Room-Temperature Quantum Hall Effect in Graphene [J].Science,2007,315:1379.

[8] Watanabe K,Taniguchi T,Kanda H.Direct-Bandgap Properties and Evidence for Ultraviolet Lasing of Hexagonal Boron Nitride Single Crystal [J].Nat Mater,2004,3：404-409.

[9] WU Meng-hao,ZHANG Zhu-hua,ZENG Xiao-cheng.Charge-Injection Induced Magnetism and Half Metallicity in Single-Layer Hexagonal Group Ⅲ/Ⅴ (BN,BP,AlN,AlP) Systems [J].Appl Phys Lett,2010,97(9):093109.

[10] CI Li-jie,SONG Li,JIN Chuan-hong,et al.Atomic Layers of Hybrided Boron Nitride and Graphene Domains [J].Nat Mater,2010,9：430-435.

[11] SONG Li,Balicas L,Mowbray D J,et al.Anomalous Insulator-Metal Transition in Boron Nitride-Graphene Hybrid Atomic Layers [J].Phys Rev B,2012,86(7)：075429.

[12] YU Shan-sheng,ZHENG Wei-tao,WANG Chun,et al.Nitrogen/Boron Doping Position Dependence of the Electronic Properties of a Triangular Graphene [J].Acs Nano,2010,4(12):7619-7629.

[13] Hohenberg P,Kohn W.Inhomogeneous Electron Gas [J].Phys Rev,1964,136(3B):864-871.

[14] Perdew J P,Burke K,Ernzerhof M.Generalized Gradient Approximation Made Simple [J].Phys Rev Lett,1996,77(18):3865-3868.

[15] SUN Chang-qing,FU Shao-yuan,NIE Yan-guang.Dominance of Broken Bonds and Unpaired Nonbondingπ-Electrons in the Band Gap Expansion and Edge States Generation in Graphene Nanoribbons [J].J Phys Chem C,2008,112(48):18927-18934.

[16] Manna A K,Pati S K.Tunable Electronic and Magnetic Properties in BxNyCzNanohybrids:Effect of Domian Segregation [J].J Phys Chem C,2011,115(21):10842-10850.