基于混合杂草算法的神经网络优化策略*

彭 斌，胡常安，赵荣珍

（1.兰州理工大学数字制造技术与应用省部共建教育部重点实验室 兰州，730050）（2.兰州理工大学机电工程学院 兰州，730050）

引 言

神经网络是一个具有高度非线性的超大规模连续时间自适应信息处理系统，用分布在网络内部的联结权值表达所学习的故障诊断知识，对故障具有联想记忆、模式匹配和相似归纳等能力，可实现故障与征兆之间的非线性映射关系，特别适用于多故障、多征兆复杂模式的识别，在转子系统的故障诊断中广泛应用。在智能算法对NN的训练应用中，BP算法为最常用的训练方法，但是这种基于梯度的学习算法易陷入局部最优解。GA在建立系统层次结构、全局寻优等方面具有优点，但容易导致早熟。PSO存在一定程度的早熟和收敛慢的现象。为了探索更好、更高效的算法，许多学者进行了大量研究工作。

A.R.Mehrabian等提出了一种从自然界杂草进化原理演化而来的随机搜索算法——入侵式杂草优化算法。该算法模仿了杂草入侵的种子空间扩散、生长、繁殖和竞争性消亡的基本过程，具有很强的鲁棒性和自适应性。采用多维基准函数进行大量数值模拟和比较实验，揭示了IWO算法的特性，得到更优的结果。与GA相比，IWO算法简单、易于实现，不需要遗传操作算子，能简单有效地收敛问题的最优解，是一种强有力的智能优化工具［1］。文献［2－3］将IWO算法应用在图像聚类和求解约束性问题中，取得了不错的效果。张氢等［4］通过马尔科夫链证明了IWO算法的全局收敛性并应用于减速器质量最轻数学模型的优化。

笔者在总结归纳以往学者研究的基础上，提出了将GA的交叉算子和PSO的矢量跟踪思想引入新的HIWO算法中。用HIWO算法实现对NN的权值、阈值及结构的优化，有效避免了算法陷入局部最优解。提出了一种主副分区编码方案，将网络的拓扑结构、连接权和阈值级联分区编码。在满足某一特定性能指标的前提下，采用HIWO算法寻找全局最优解，并给出了HIWO动态创建网络参数的整体算法。通过对故障信号分类的仿真，并与GA，PSO和IWO的结果进行对比，验证了新方法的优越性和有效性。

1 神经网络

NN是由多个非常简单的处理单元彼此按某种方式互相连接而成的一种非线性动力学网络系统。系统靠其状态对外部输入信息的动态响应来处理信息，具有高度并行处理能力。该系统模拟人的大脑神经元结构特征建立，可看成为从输入到输出的高度非线性映射。目前，NN的优化研究主要集中在前馈NN－BP上，标准BPNN由3层神经元组成（输入层、隐含层和输出层）。网络中相邻层采用全互连方式连接，同层各神经元没有连接，输出层和输入层之间没有直接的联系，结构如图1所示。

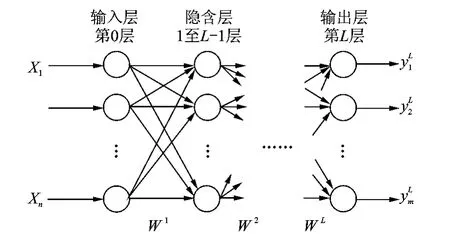
图1 标准BPNN结构

假设网络有n个输入和m个输出，则其作用可看作是由n维欧氏空间到m维欧氏空间的一个非线性映射。许多研究表明，只要隐层的神经元个数足够多，则这种映射可以逼近任何连续函数。

人工神经网络的数学模型为

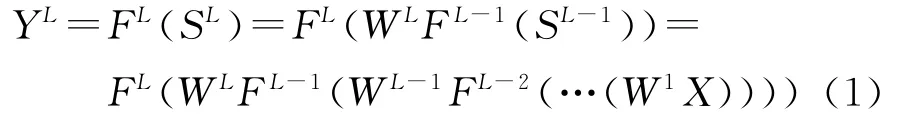
其中：X＝［x1，x2，…，xn］T为输入；Y＝［y1，y2，…，ym］T为输出；F（·）为激活函数；S为神经元的激活水平；W 为权重，表示输入层神经元与隐层神经元以及隐层神经元与输出层神经元之间的联接强度。

网络输出仅与输入及网络权重有关，输出为输入的显式表达。

BP网络模型处理信息的基本原理是：输入信号xi通过中间节点（隐层点）作用于输出节点，经过非线形变换，产生输出信号ym。通过调整输入节点与隐层节点的联接强度取值Wij和隐层节点与输出节点之间的联接强度以及阈值，使误差沿梯度方向下降。经过反复学习训练，确定与最小误差（网络输出值y与期望输出值t之间的偏差）相对应的网络参数（权值和阈值），训练即告停止。

BP算法本质上为梯度下降法，它要优化的目标函数非常复杂，在进行全局搜索时，不可避免地存在收敛速度慢的问题。此外，BP算法是一种局部搜索的优化方法，在求解复杂非线性函数的全局极值时，算法有可能陷入局部极小值，导致训练失败。

2 IWO算法

IWO算法是一种非常新颖而高效的全局优化算法［2］。该算法模拟杂草克隆、占地、生长并繁殖的自然行为，具体的实现步骤如下。

1）初始化种群：初始种群大小n－ini、最大迭代次数itermax、问题的求解维数dim、最大种群数量plant－max－no、最大种子数seedmax、最小种子数seedmin、自变量初始搜索空间最小值xmin及最大值xmax、非线性调制指数n、初始标准差σinitial和最终标准差σfinal。

2）根据初始种群、自变量初始搜索空间以及问题的求解维数随机产生初始解。

3）进化代数的更新及子代个体正态分布的标准差计算。其计算公式为

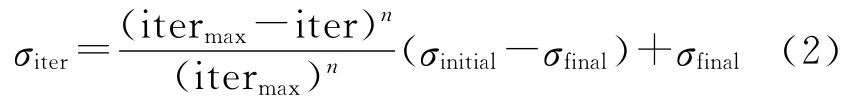
其中：iter为当前的迭代次数。

4）子代的繁殖，子代个体按照正态分布N（0，σ2）随机扩散在父代个体周围。在计算子代个体（种子数）时，根据其适应值的优劣来决定繁殖个数。最优适应值个体允许繁殖的子代个数为seedmax，最差适应值个体允许繁殖的子代个数为seedmin，其他个体允许繁殖的子代个数与其适应值服从向下取整的线性关系。这种机制在加强优秀个体局部搜索能力的同时，兼顾群体的多样性，与自然界杂草群落真实发生的状况更为相似，其繁殖操作如图2所示。

图2 父代个体繁殖产生种子的过程示意图

5）判断是否达到最大种群数量，在未达到最大种群数量时重复操作步骤4。

6）当超过最大种群数量时，竞争淘汰，适者生存。将父代个体和子代个体按适应值优劣排序，保留适应值优秀的个体，使种群数目保持在最大种群数量以内，精英个体在操作中被自动保留到下一代，从而保证了算法的收敛性。

7）判断是否达到最大种群数，未达到时重复步骤4～6，反之则将适应值最优个体输出作为最优解。

3 基于HIWO－NN的模型设计

3.1 基本原理

HIWO算法构建NN结构参数的基本原理是利用杂草进化的优点，将网络的拓扑结构、连接权及阈值连成主副分区编码串而构成进化的初始群体。通过杂草繁殖操作，在满足某一特定性能指标的前提下寻找全局最优解。该最优解的编码串经解码即为特定求解问题的合适NN结构参数。图3为基于HIWO－NN的模型设计流程图。

3.2 BPNN结构设计

3.2.1 拓扑结构

由Kolmogarav定理可知在有合理的结构和恰当权值条件下，3层前向网络能以任意精度逼近有界非线性函数，在此设计3层神经网络结构来进行优化训练［5－6］。

3.2.2 隐层节点数

在BP网络中，隐层节点数的选择非常重要。为尽可能避免训练时出现过拟合现象，保证足够高的网络性能和泛化能力，确定隐层节点数的最基本原则是：在满足精度要求的前提下，取尽可能少的隐层节点数。若隐层节点数太少，网络可能根本不能训练或网络性能很差；若隐层节点数太多，虽然可使网络的系统误差减小，但也会使网络训练时间延长。另一方面，训练容易陷入局部极小点而得不到最优点，同时也是训练时出现过拟合的内在原因。

隐层的节点数选择并没有固定模式可取，合理的隐层节点数应在综合考虑网络结构复杂程度和误差大小的情况下确定。

3.3 传递函数的选择

任何的数学函数只要满足定义域为全体实数且其傅里叶展开式不是完备的正交集函数，都可以作为NN的传递函数，从而得到性能不同的NN，满足实际的需求。

BP网络的传递函数（又称激活函数）有十几种，经常采用的有对数Sigmoid函数（logsig）、正切Sigmoid函数（tansig）和线性函数（purelin）

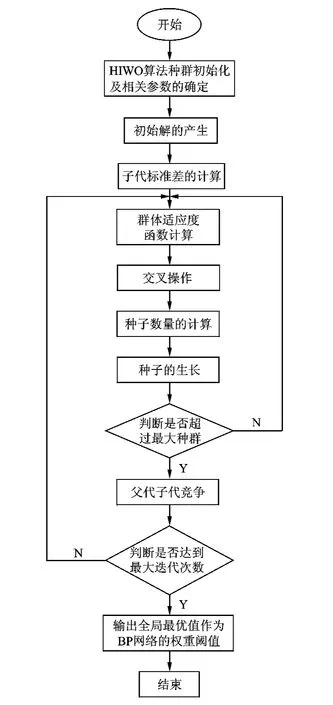
图3 基于HIWO－NN的模型设计流程图

在实际的应用中要根据具体输出情况选择：对数Sigmoid函数将输出值限定在0到1之间；正切Sigmoid函数将输出值限定在－1到1之间；purelin线性函数的输出和输入相同。

3.4 HIWO算法设置

3.4.1 编码

IWO算法中正态分布采用实数编码，所以这里主编码采用实数编码。

N，L和M分别代表NN的输入层、隐层和输出层个数，整个主编码由4部分组成，如图4所示。

图4 主编码构成

HIWO算法的种群维数D＝N×L＋L＋L×M＋M。其中：N和M相对固定，大小由具体问题的输入与输出参数个数决定；A区为输入层节点到隐层的连接权编码，aij为输入层第i节点同隐层第j节点的连接权编码；B区为隐层节点的阈值编码，bi为隐层第i节点的阈值编码；C区为隐层节点到输出节点的连接权编码，cij为隐层第i节点同输出层第j节点的连接权编码；D区为输出节点各神经元的阈值编码，di为输出层第i节点的阈值编码。

HIWO算法的初始编码以充分大的隐层个数L及层间全相连的方式组成初始群体。副编码为0和1组成的矩阵，维数与主编码一致，初始设定为全1矩阵表示全连接，在求解中与主编码相乘。随着进化过程中自适应调整隐层节点数L及删去部分层间的连接权，实现自适应地动态改变编码长度。

3.4.2 适应度函数

HIWO算法的适应度函数F（即NN性能评价函数）是算法指导搜索的惟一信息，它的选取是算法好坏的关键。适应度函数要能有效地指导搜索沿着优化参数组合的方向，逐渐逼近最佳参数组合，而不会导致搜索不收敛或陷入局部最优的状况，同时也要求这个函数易于计算。

NN的目标函数E定义为：在所有的进化代数中搜索网络误差最小的权重。HIWO算法的适应度函数和NN的目标函数有着必然的联系。HIWO算法用来求解最小值问题，它的适应度函数定义为NN的目标函数，表达式为

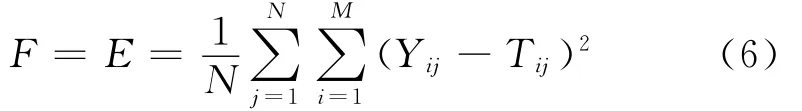
其中：N为测试样本数；M为网络输出神经元的个数；Yij为第j个样本的第i个网络输出节点的理想输出值；Tij为第i个网络输出节点的实际输出值。

HIWO算法的适应度函数与GA的适应度函数互为倒数，这是因为GA只能朝着适应度函数值增大的方向进化［7］。

3.4.3 子代的矢量跟踪

HIWO算法借鉴PSO算法中速度更新公式中的“社会”部分，子代在繁殖的过程中不仅正态分布于父代周围，而是也有向群体或邻域历史最佳位置逼近的趋势。

3.4.4 交叉操作

交叉操作通过种群中两个个体随机交换遗传信息，形成两个相似的后代。主要目的是通过重新组合以进化出适应度更高的个体。将GA中的交叉算子引入到IWO算法，避免了算法的早熟收敛，提高了算法的性能。通过交叉操作，不仅能够产生新的个体，更能够在父代与子代竞争之前，对所有个体进行二次选择［8－9］。具体步骤：对父代和子代的所有个体取适应值较差的后一半种群进行相邻交叉操作，交叉前和交叉后的适应值排序比较，取优秀个体。

3.4.5 其他HIWO算法参数的设置

杂草种群的增加并不提高寻优成功率，非线性调制指数n对IWO算法的收敛起着关键作用［1］。在求解高维问题时，一般参数设置如表1所示。

表1 高维问题求解参数设置

4 数值仿真及应用实例

为了验证HIWO算法创建NN的可行性及有效性，以转子实验台模拟6类故障数据的4类谱熵为训练样本，应用Matlab软件进行仿真分析。

转子实验台如图5所示。实验台在不同的位置布置了13个通道的电涡流传感器，其中：1～12号电涡流传感器采集转子的振动信号；13号采集转速信号。分别模拟6类故障：转子不对中、质量不平衡、动静碰磨、松动、油膜涡动和油膜振荡。选取转速为2.8kr／min的实验数据作为原始数据，选取其中一个通道的3 000组数据，经过中值滤波、去直流分量和小波消噪，计算其奇异值谱熵、功率谱熵、小波能谱熵和小波空间谱熵4类谱熵，并对样本数据进行归一化处理，并将其作为HIWO－NN的训练样本。

初始网络结构输入层为4，隐层为8，输出层为1。输出层的设计归一化至0.4～0.9之间的一组数据。选取60组数据作为训练样本，HIWO算法的初始种群为5，最大迭代次数为300，最大种群数目为30，最大种子数为4，最小种子数为0，非线性调制指数为2.3，初始标准差为5，最终标准差为0.01，初始搜索空间最大值为1，最小值为－1，交叉概率为0.9，学习因子为1。IWO的参数设置与HIWO相同，但没有交叉概率和学习因子。GA的种群大小为40，交叉概率为0.75，变异概率为0.1。PSO的种群大小为40，初始惯性权重为0.7，学习因子均为1.5，最大飞行速度限制为0.1。对4种算法的初始解都采用网格分布法，输入层与隐层之间、隐层与输出层之间的传递函数都是采用对数Sigmoid函数［10－12］。

图5 转子实验台

图6为4种算法的迭代误差比较结果。可以看出，128代之前有交叉优势的PSO和HIWO占有较大优势，128代之后HIWO算法占有绝对优势。在对NN的训练中，HIWO算法将隐层连接权优化到39个，PSO算法和IWO算法将隐层连接权优化到42个，GA将隐层连接权优化到45个。

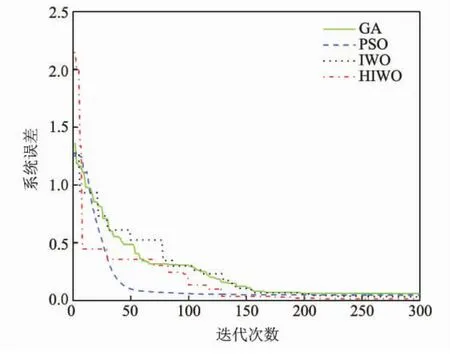
图6 迭代误差比较

图7为不同运行次数下的误差比较。总体上，HIWO算法比其他3种算法能更精确地收敛到较低的误差。

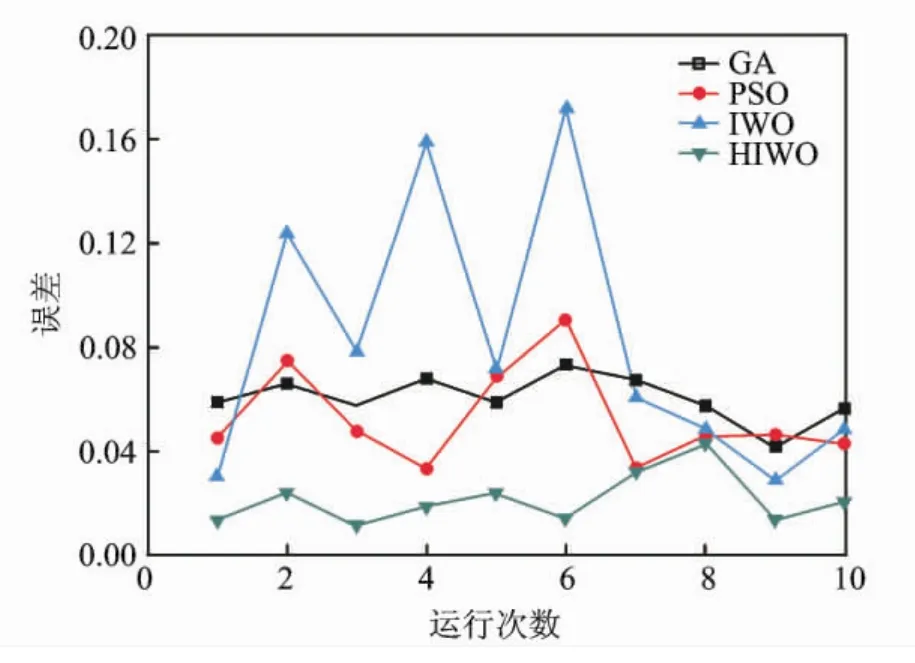
图7 不同运行次数下迭代误差比较（迭代次数为300）

5 结束语

IWO算法是一种高效的随机智能优化算法，以群体中优秀个体来指导种群的进化，以正态分布的方式将子代个体叠加在父代个体周围，通过标准差的动态调整，兼顾了群体的多样性和选择力度。

仿真结果表明，提出的HIWO算法既能构建网络结构，又能起到网络学习的作用，相比GA，PSO和IWO在搜索精度上有显著提高，且极易摆脱局部极小的困扰。同时，采用HIWO算法自学习构建NN结构的方法能大大减少NN的连接权，缩短对NN的训练时间。

随着函数维数和群体规模的增加，如何有效缩短算法的运行时间和提高求解精度是今后研究的方向之一。目前，IWO算法的研究与应用仍有限，IWO算法的理论以及与其他算法的有效混合及应用都有待进一步研究。

［1］ Mehrabian A R，Lucas C.A novel numerical optimization algorithm inspired from weed colonization［J］.Ecological Informatics，2006，1（4）：355－366.

［2］ 苏守宝，方杰，汪继文，等.基于入侵性杂草克隆的图像聚类方法［J］.华南理工大学学报：自然科学版，2008，36（5）：95－100.Su Shoubao，Fang Jie，Wang Jiwen，et al.Image clustering method based on invasive weed colonization［J］.Journal of South China University of Technology：Natural Science Edition，2008，36（5）：95－100.（in Chi－nese）

［3］ Su Shoubao，Wang Jiwen，Zhang ling，et al.An invasive weed optimization algorithm for constrained engineering design problems［J］.Journal of University of Science and Technology of China，2009，39（8）：885－893.

［4］ 张氢，陈丹丹，秦仙蓉，等.杂草算法收敛性分析及其在工程中的应用［J］.同济大学学报：自然科学版，2010，38（11）：1689－1693.Zhang Qing，Chen Dandan，Qin Xianrong，et al.Convergence analysis optimization algorithm in engineering of invasive weed and its application［J］.Journal of Tongji University：Natural Science Edition，2010，38（11）：1689－1693.（in Chinese）

［5］ 刘亮，李龙澍.基于神经网络和遗传算法的RoboCup截球策略［J］.计算机工程与应用，2006，42（33）：28－30.Liu Liang，Li Longshu.Intercept strategy based on neural network and genetic algorithms in RoboCup［J］.Computer Engineering and Applications，2006，42（33）：28－30.（in Chinese）

［6］ 李振涛，王淑玲，张国立.利用遗传模拟退火算法优化神经网络结构［J］.计算机工程与应用，2007，43（36）：74－76.Li Zhentao，Wang Shuling，Zhang Guoli.Application genetic and simulated annealing algorithm for optimization of neural network structure［J］.Computer Engineering and Applications，2007，43（36）：74－76.（in Chinese）

［7］ 梁艳春，吴春国，时小虎.群智能优化算法理论与应用［M］.北京：科学出版社，2009：19－25.

［8］ 王晶，张庆，梁霖，等.采用遗传算法的自适应随机共振系统弱信号检测方法研究［J］.西安交通大学学报，2010，44（3）：32－36.Wang Jing，Zhang Qing，Liang Lin，et al.Adaptive stochastic resonance based on genetic algorithm with applications in weak signal detection［J］.Journal of Xi′an Jiaotong University，2010，44（3）：32－36.（in Chinese）

［9］ 程力旻，谢志江，刘利云，等.运用免疫遗传神经网络的汽轮机振动故障诊断［J］.振动、测试与诊断，2010，30（6）：675－678.Cheng Limin，Xie Zhijiang，Liu Liyun，et al.Vibration fault diagnosis of steam turbine using immune genetic neural networks［J］.Journal of Vibration，Measurement ＆ Diagnosis，2010，30（6）：675－678.（in Chinese）

［10］霍天龙，赵荣珍，胡宝权.基于熵带法与PSO优化的SVM转子故障诊断［J］.振动、测试与诊断，2011，31（3）：279－284.Huo Tianlong，Zhao Rongzhen，Hu Baoquan.Fault diagnosis for rotor systems based on entropy band method and support vector machine optimized by PSO［J］.Journal of Vibration，Measurement ＆Diagnosis，2011，31（3）：279－284.（in Chinese）

［11］Pourjafari E，Mojallali H.Solving nonlinear equations systems with a new approach based on invasive weed optimization algorithm and clustering［J］.Swarm and Evolutionary Computation，2012，4：33－43.

［12］Peng Bin，Hu Changan，Zhao Rongzhen，et al.The investigation of fault diagnosis based on GA－HPSONN［J］.Journal of Computers，2012，7（10）：2511－2517.