柔性转子无试重模态动平衡方法与试验*
2013-12-03李晓丰郑龙席刘振侠
李晓丰,郑龙席,刘振侠
(西北工业大学动力与能源学院 西安,710072)
引 言
在航空发动机故障中,会出现因转子振动过大而引起整机振动超标、导致转子零部件变形和应力超限而损坏的情况。严重时甚至会因转子振动剧烈导致轴承负荷过大,出现轴承抱死、转轴瞬间断裂的现象[1-2]。转子振动的大小在一定程度上影响发动机转子部件与静子部件的间隙设计。间隙设计过大则发动机效率降低,设计过小则动、静件易碰摩。为保证转子设备能在工作转速下稳定运行,必须对其严格实施动平衡。传统转子动平衡方法有模态平衡法和影响系数法。邓旺群等[3-5]采用影响系数法对某型涡轴发动机动力涡轮转子进行了高速动平衡,使发动机整机振动得到了控制。郑龙席等[6]采用影响系数法对一微型涡喷发动机进行了现场瞬态动平衡,有效控制了发动机的振动。传统动平衡方法需添加试重,多次起车才能达到平衡的效果,平衡效率低、工序复杂,对技术人员要求具有丰富的平衡经验,且影响系数法在多平面平衡时,影响系数矩阵非常敏感,易带来错误的平衡信息[7]。此外,添加试重可能会额外增加转子的不平衡量大小,易导致转子在平衡过程中因振动过大而损坏,增加了平衡风险。
无试重动平衡方法对转子实施动平衡时不需添加任何试重,可减小发动机转子开起次数,降低平衡风险,提高平衡效率。文献[8-10]进行基于模态平衡方法的无试重动平衡理论与试验研究。文献[11]结合模态平衡法和影响系数法,提出了一种低速转子的无试重动平衡方法。徐宾刚等[12]开展了基于影响系数法的柔性转子无试重动平衡理论与方法研究。
笔者在模态动平衡理论的基础上,推导出一种高速柔性转子无试重模态动平衡方法。结合有限元分析技术,在一高速柔性模拟转子试验器上进行了动平衡试验研究。
1 无试重动平衡理论与方法
实际发动机转子的质心连线是一条复杂的空间曲线,不易直接分析转子的不平衡量。假设一发动机转子已经过多平面高速动平衡,对其进行受力分析,不平衡量分布如图1所示。平衡后转子的不平衡激振力主要由两部分组成:a.原有转子连续分布的不平衡力ω2U(z);b.集中作用的校正力ω2Ud,其中,Ud为平衡转子时在不同平衡平面添加的校正量。
利用振动系统各阶主振型的正交性[7],可将转子的不平衡量按主振型函数进行分解
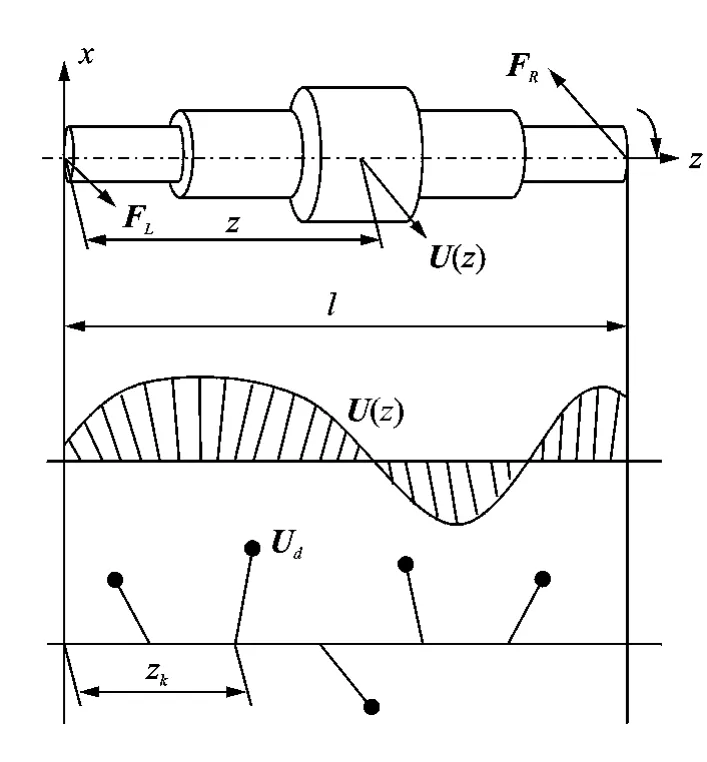
图1 平衡后转子不平衡量分布
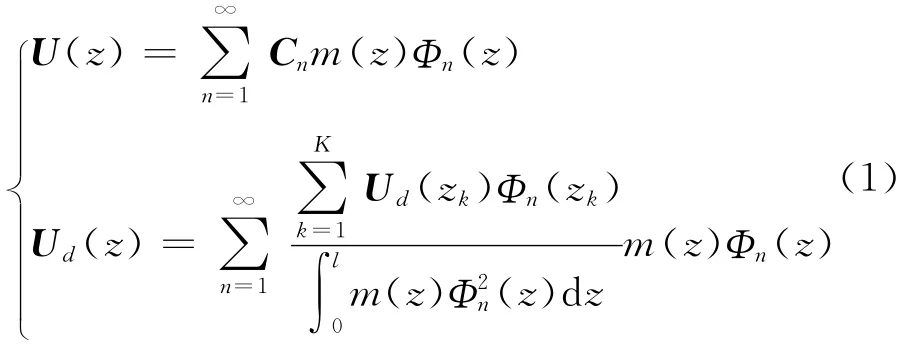
其中:Cn为第n阶主振型系数;m(z)为转子的物理质量;Φn为转子的第n阶模态振型函数。
转子的质心偏心曲线为
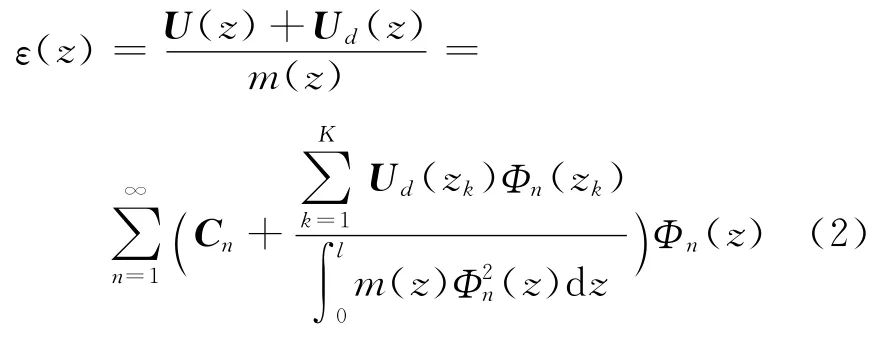
其中:ε(z)为转子z位置处的质心偏心。
要使柔性转子达到平衡,转子必须满足支承处反力为零。由力矩平衡得到转子两支承处的动反力为
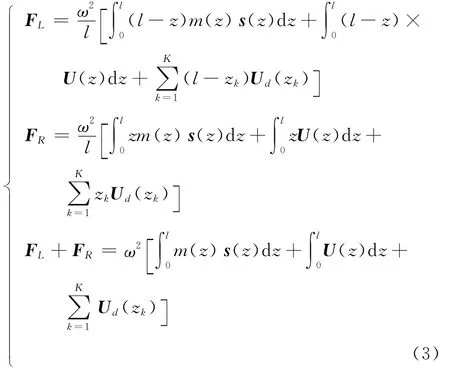
其中:s(z)为转子z位置处的振动,包括大小和方位;ω为转子的转速。
求解转子运动微分方程,得到转子振动与不平衡量之间的关系[7]为
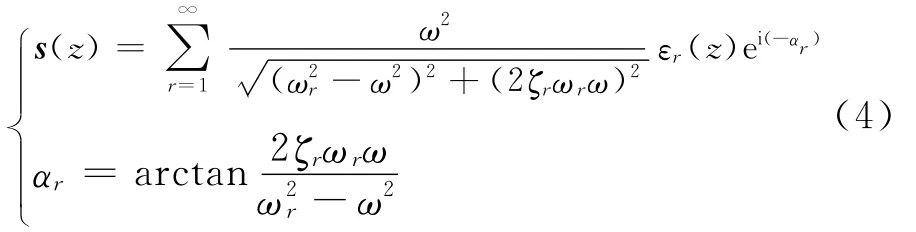
其中:ωr为转子第r阶固有频率;ζr为转子第r阶模态阻尼。
令
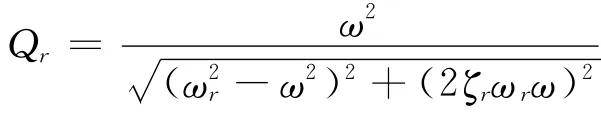
称Qr为转子的第r阶振动放大因子。
将式(2)代入式(4),转子的振动可写为
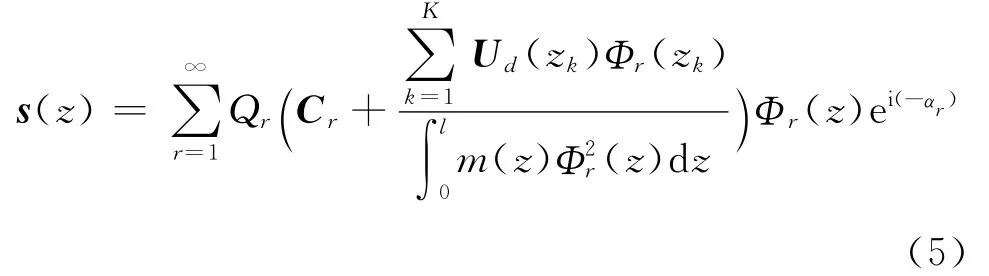
将式(5)代入式(3),则支承处的动反力可写为

令FL=0,FR=0,FL+FR=0,得到
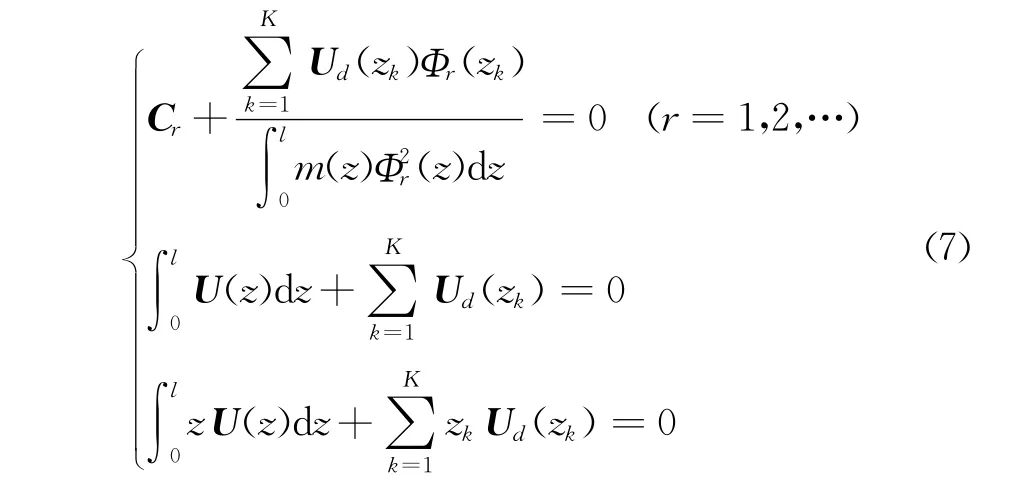
因转子在平衡前未添加任何校正量,则Ud=0。当ω=ωr时,式(5)可简化为
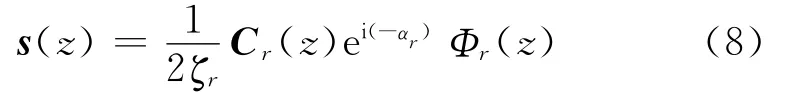
则
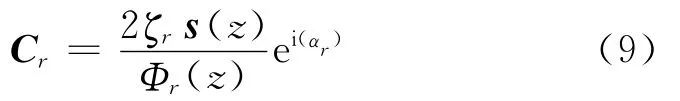
结合式(7)和式(9),当采用N平面对转子第r阶不平衡量进行动平衡时,校正量需满足
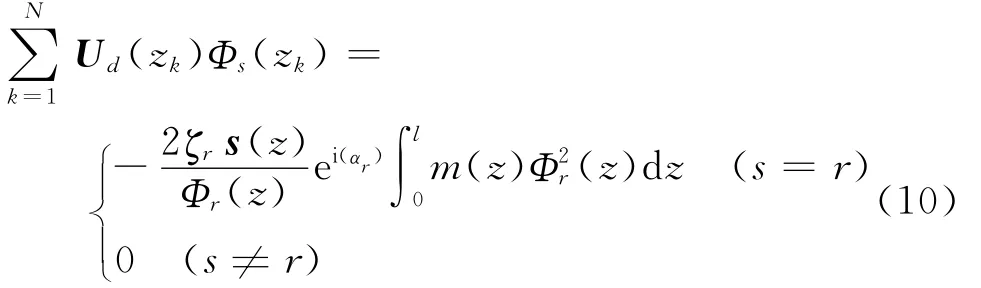
其中:s=1,2,…,N。
当采用N+2平面平衡法时,校正量需满足
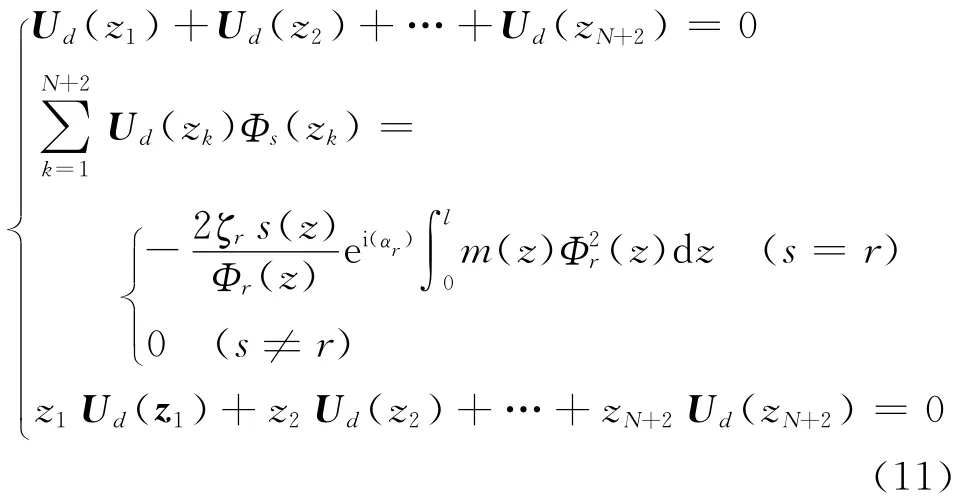
其中:s=1,2,…,N。
2 无试重动平衡试验
高速柔性模拟转子的物理模型如图2(a)所示,试验器如图2(b)所示。实验室转子试验器支承为滑动轴承,支承刚度K1=K2=1.1×106N/m,简支盘的直径D1=0.076m,宽度h1=0.024m,悬臂盘的直径D2=0.076m,宽度h2=0.018m,轴的直径d=0.009m,转轴总长L=0.45m,L1=0.052m,L2=0.114m,L3=0.112m,L4=0.04m,L5=0.04 m,转轴转接段的直径D2=0.024m,转接段的长度为0.032m。转子通过联轴器直接与变频电机连接,动力从左端输入,电机设计最高转速为10kr/min。转子轴及转接段的材料弹性模量E=2.1×1011N/m2,密度为8 200kg/m3,泊松比为0.3,盘的材料弹性模量E=2.1×1011N/m2,密度为8 300kg/m3,泊松比为0.3。

图2 高速柔性模拟转子
利用有限元分析软件Samcef For Rotor建立模拟转子的三维实体有限元模型,对其进行临界转速和模态分析,得到模拟转子系统一阶临界转速为3.249kr/min。转子的前二阶模态振型如图3所示,可以看出,模拟转子的一阶模态所对应的频率为53.6Hz,即3.216kr/min,二阶模态所对应的频率为122.3Hz,即7.338kr/min。
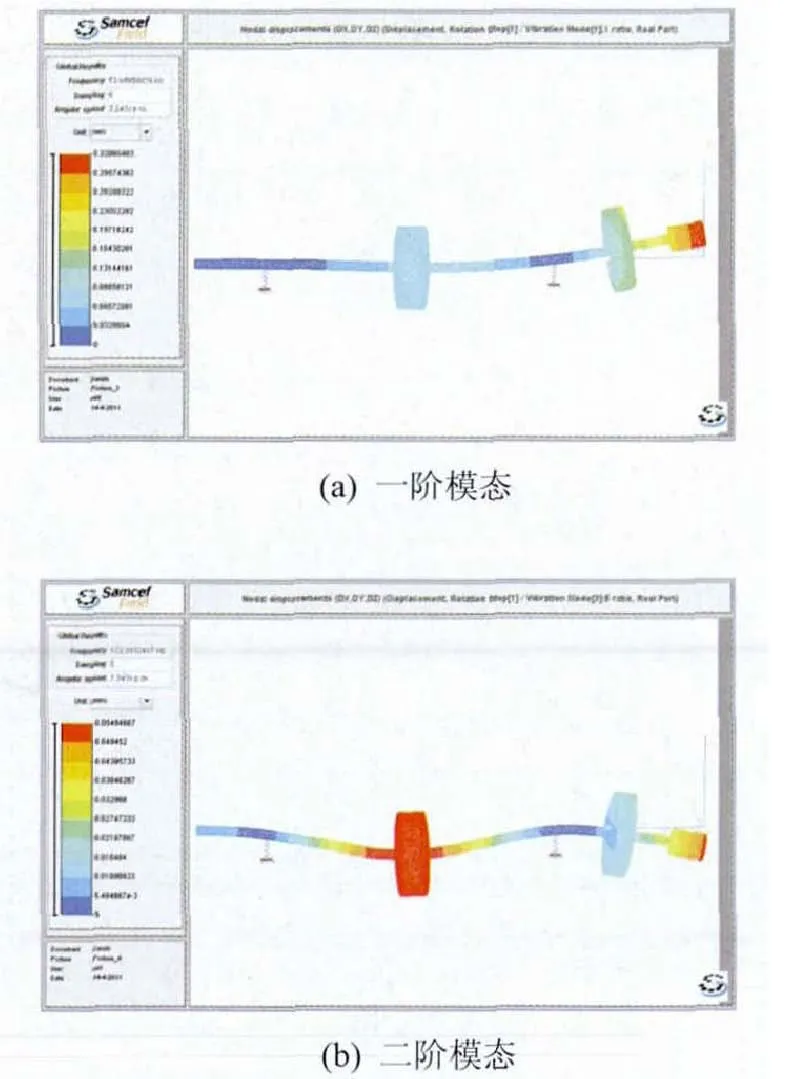
图3 高速柔性模拟转子系统模态振型图
从转子的模态振型图可以看出:转子在一阶临界转速时,转接段(悬臂端)是转子振动最大的地方,两滑动轴承之间简支轴段部分,简支盘处振动最大,但悬臂盘处振动明显大于简支盘,悬臂轴段的振动与两轴承间简支轴段的振动方向相反;在二阶临界转速时,简支盘和转接段(悬臂端)是转子振动最大的地方,简支盘的振动明显大于悬臂盘,且悬臂轴段的振动和简支轴段的振动方向相同。该模态分析结果揭示了高速柔性模拟转子在实际运行过程中最易出现问题的几个位置,为提高转子运行安全性提供了参考依据。
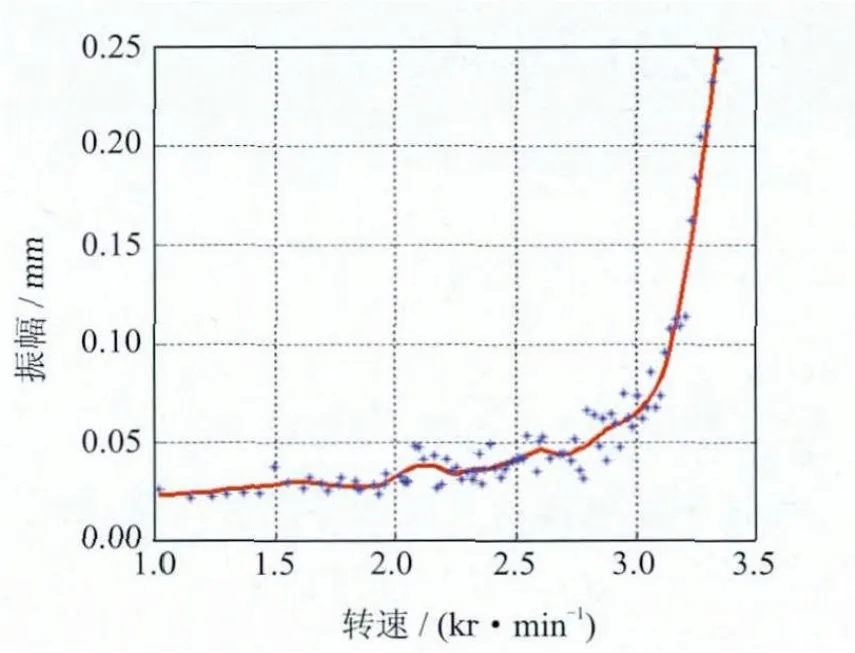
图4 模拟转子简支盘水平方向瞬态响应曲线
图4为模拟转子平衡前简支盘水平方向的不平衡瞬态响应。可以看出,简支盘水平方向振动一直随着转速的升高而增加,升速达到3.3kr/min时,振动超过限幅值0.25mm,这说明转子在临界转速附近振动非常大,不能安全跨过一阶临界转速。利用转子在水平方向上测得的不平衡瞬态响应振幅数据,计算出转子的一阶模态阻尼为0.24。选定转子的平衡转速为3.2kr/min,再次开启转子,将转速稳定在3.2kr/min附近,测试一组转子不平衡稳态响应曲线,如图5(b)所示。在平衡转速下模拟转子简支盘水平方向振幅为0.18mm∠190°,将其代入式(10),以简支盘作为平衡平面,平衡半径为30mm,计算得到应在简支盘275°添加0.712g校正质量。在实际平衡过程中,在简支盘275°添加了两对螺栓和螺母,每对螺栓和螺母的质量为0.25g,共添加了0.5g校正量。
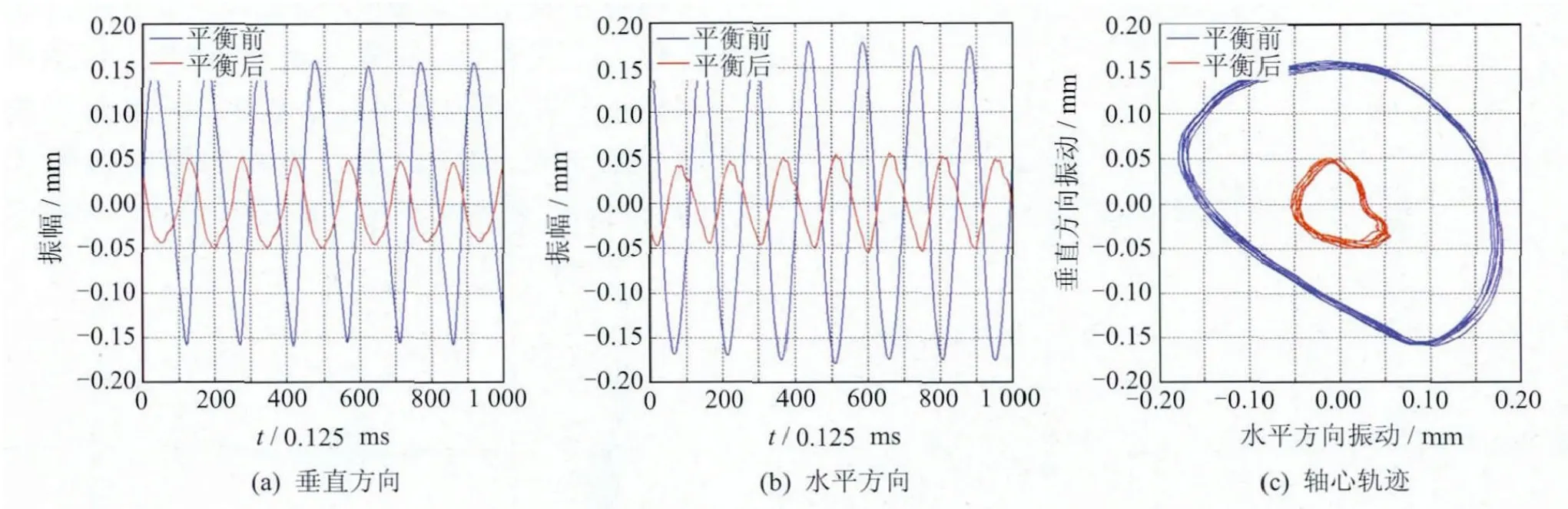
图5 模拟转子简支盘稳态响应平衡前后对比
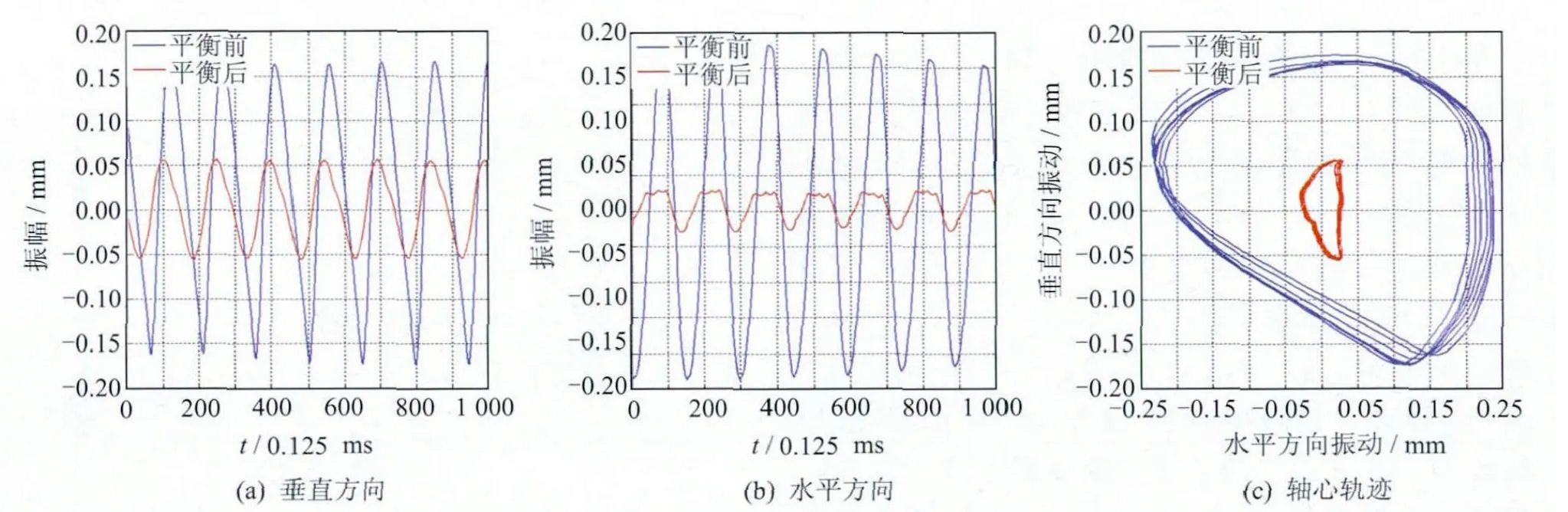
图6 模拟转子悬臂盘稳态响应平衡前后对比
平衡前、后模拟转子的振动对比如图5~8所示。图5~6为模拟转子稳态响应平衡前后的对比。从图5可以看出,经平衡后转子简支盘水平方向振幅从0.18mm降低到0.05mm,降幅为72.2%,垂直方向振幅从0.155mm降低到0.05mm,降幅为67.7%,简支盘振幅平均降低70%。从图6可以看出,经平衡后转子悬臂盘水平方向振幅从0.24mm降低到0.025mm,降幅为89.6%,垂直方向振幅从0.16mm降低到0.05mm,降幅为68.8%,振幅平均降低79.2%。
图7~8为模拟转子瞬态响应平衡前后的对比。可以看出,转子在平衡前因振幅超限,无法安全通过3.3kr/min,经对转子实施一次单平面无试重平衡后,转子过临界时简支盘和悬臂盘振幅都有明显下降,简支盘最大振幅为0.06mm,悬臂盘最大振幅仅有0.04mm,而转子初始弯曲就有0.02mm,残余不平衡量仅为5g·mm,按平衡精度计算达到了G2.5等级,转子能安全跨过一阶临界转速,平衡效果显著。
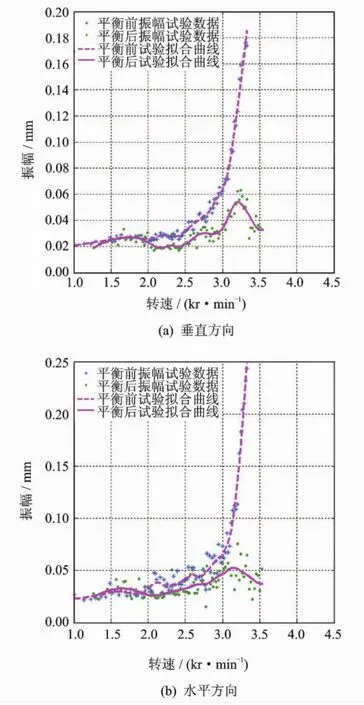
图7 模拟转子简支盘瞬态响应平衡前后对比
3 结束语
以一平衡后的转子系统作为研究对象,从转子不平衡量分布的特点出发,得到转子在不平衡力激振下两支承处的受力方程。利用转子平衡时支承反力为0的平衡条件,推导出平衡转子所需添加校正量的大小和方位。该方法是在模态平衡法的基础上建立起来的,仅需结合有限元分析软件准确获取转子的临界转速、各阶模态振型函数等动力学特性,不需添加任何平衡试重,开起转子两次,即可求得各平衡平面所需添加校正量的大小和方位。
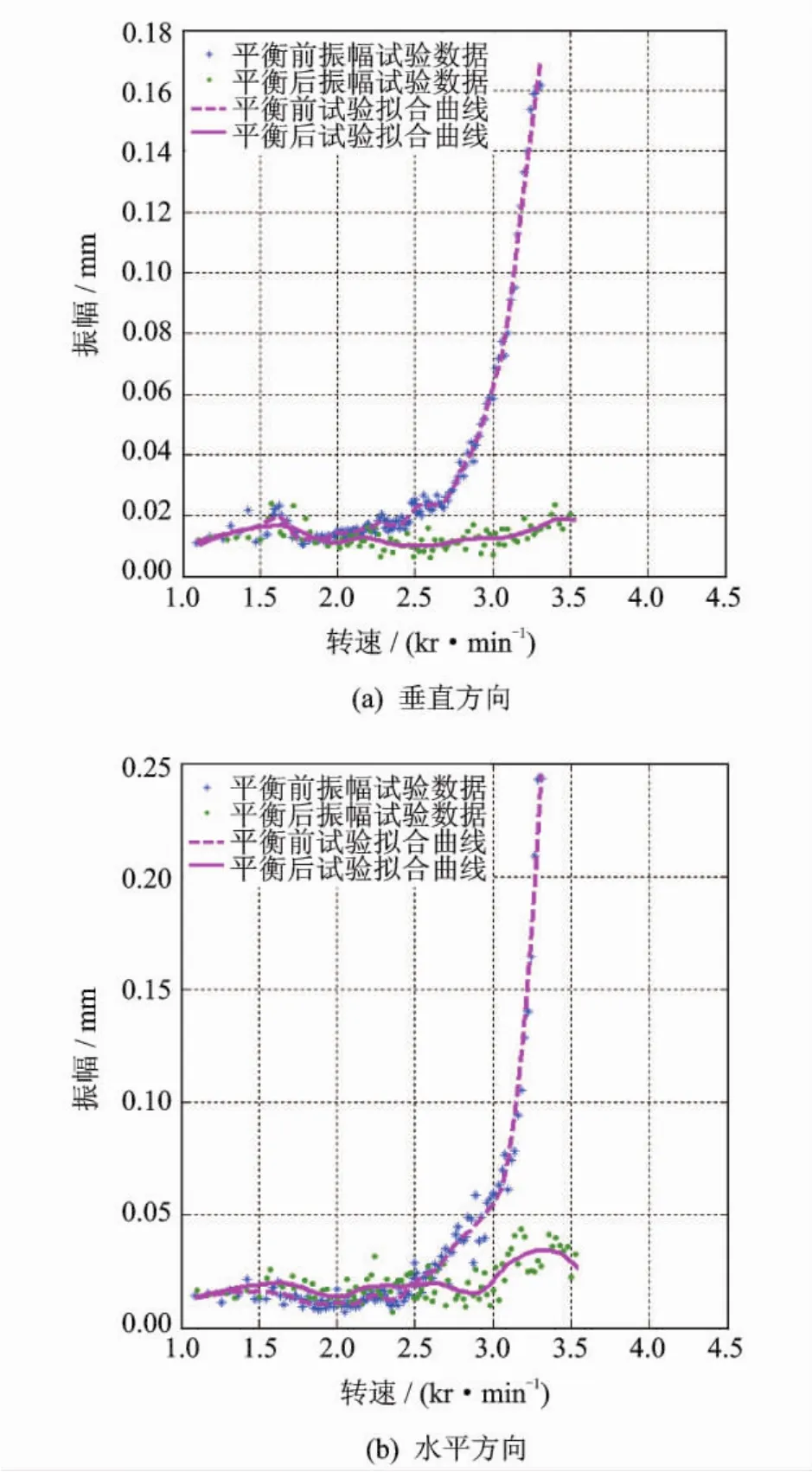
图8 模拟转子悬臂盘瞬态响应平衡前后对比
利用该无试重动平衡方法在一高速柔性模拟转子试验器上进行了一阶临界转速动平衡试验。一次平衡后转子在平衡转速下振幅平均降低在70%以上,残余不平衡量仅有5g·mm,平衡精度达到了G2.5级。试验验证了该方法的正确性,同时说明该方法是一种较实用的平衡方法,省去了传统平衡方法需要添加试重的平衡工序,无需多次重复起车,简化了平衡步骤,提高了平衡效率。对于同一类型转子,各阶模态振型函数可建立数据库,不需重复建立有限元模型,在实际平衡时只需调用数据库里的振型函数即可,达到一次建立终身受用的效果。由于转子试验器的限制,本试验仅对跨一阶柔性转子的无试重动平衡理论与方法进行了验证。
[1] 尹泽勇,付才高,李其汉,等.《航空发动机设计手册》第19册——转子动力学及整机振动[M].北京:航空工业出版社,2000:1-7.
[2] 闻邦椿.高等转子动力学:理论、技术与应用[M].北京:机械工业出版社,1999:310-318.
[3] 邓旺群,高德平,刘金南,等.转子高速动平衡技术在涡轴发动机整机减振中的作用[J].航空动力学报,2005,20(1):78-85.Deng Wangqun,Gao Deping,Liu Jinnan,et al.Effect of high speed dynamic balance technique on turboshaft engine vibration reduction[J].Journal of Aerospace Power,2005,20(1):78-85.(in Chinese)
[4] 邓旺群,高德平.应用于小发柔性转子的高速动平衡技术[J].燃气涡轮试验与研究,2003,16(2):30-33.Deng Wangqun,Gao Deping.High speed dynamic balance technique applied to flexible rotors of a small sized engine[J].Gas Turbine Experiment and Research,2003,16(2):30-33.(in Chinese)
[5] 邓旺群,唐广,高德平.转子动力特性及动平衡研究综述[J].燃气涡轮试验与研究,2008,21(2):57-62.Deng Wangqun,Tang Guang,Gao Deping.Research summary of rotor dynamic char acteristics and dynamic balance[J].Gas Turbine Experiment and Research,2008,21(2):57-62.(in Chinese)
[6] 郑龙席,高晓果,李晓丰.某微型涡喷发动机现场瞬态动平衡技术[J].振动、测试与诊断,2008,28(3):282-285.Zheng Longxi,Gao Xiaoguo,Li Xiaofeng.Transient field balancing technique for a micro turbo-jet engine[J].Journal of Vibration,Measurement &Diagnosis,2008,28(3):282-285.(in Chinese)
[7] 安胜利,杨黎明.转子现场动平衡技术[M].北京:国防工业出版社,2007:12-27.
[8] Palazzolo A B,Gunter E J.Modal balancing of a multi-mass flexible rotor without trial weights [R].New York:[s.n.],1982.
[9] Wiese D.Two new procedures to balance flexible rotors without test runs[C]∥Proceedings of the 5th International Conference on Vibrations in Rotating Machinery.London:[s.n.],1992:557-568.
[10]Kreuzinger J T,Irretier H.Unbalance identi?cation of flexible rotors based on experimental modal analysis[C]∥Proceedings of the 7th International Conference on Vibrations in Rotating Machinery.London:[s.n.],2000:335-346.
[11]Tan S G ,Wang X X.A theoretical introduction to low speed balancing of flexible rotors:unification and development of the modal balancing and influence coefficient techniques [J].Journal of Sound and Vibrations,1993,168(3):385-394.
[12]徐宾刚,屈梁生,孙瑞祥,等.基于影响系数法的柔性转子无试重平衡法研究[J].西安交通大学学报,2000,34(7):63-67.Xu Bingang,Qu Liangsheng,Sun Ruixiang,et al.Balancing of flexible rotors without test weights[J].Journal of Xi′an Jiaotong University,2000,34(7):63-67.(in Chinese)
