双头双螺杆泵转子型线分析及建模

赵巧兰，郭津津

(天津理工大学复杂系统控制理论及应用重点实验室，天津 300384)

0 前言

双螺杆泵可应用在非润滑性介质、腐蚀性介质、含微量杂质、大流量和气液混输的工况下。其核心部件为相互啮合的双螺杆转子，转子的齿面与转子轴线垂直面的截交线称为转子型线，转子型线的设计直接影响着双螺杆泵的性能。不同的转子型线组合构成了不同类型的双螺杆泵。因此，双螺杆泵转子型线的研究是双螺杆泵研究的基础，也是双螺杆泵优化设计、提高整机性能的关键。根据转子型线的组合形式，双螺杆泵一般分为“方牙形”双螺杆泵、A型双螺杆泵、B型双螺杆泵、C型双螺杆泵和Ω型双螺杆泵。

本文以Ω型双螺杆泵转子为研究对象，其型线为普通外摆线和伸长外摆线的组合。根据摆线的相关理论知识，得出Ω型双螺杆泵转子各段型线方程，并根据包络原理求得其对应的共轭曲线方程。建立双头双螺杆泵转子三维模型并推导出螺旋曲面方程，为后续摆线型双头双螺杆泵的性能研究奠定基础。

1 螺杆螺旋端面的型线组成及方程

螺杆螺旋端面型线主要是摆线组合而成的abc曲线，如图1所示，其中ab曲线为普通外摆线，bc曲线为伸长外摆线。在螺杆端面以O1X轴为横轴、O1Y轴为纵轴建立坐标系XO1Y，同时，将坐标系XO1Y逆时针旋转角度θbc即是坐标系X'O1Y'。

图1 螺杆螺旋端面的齿形曲线Fig.1 Toothed curve of the screw's end surface

1.1 普通外摆线ab

以螺杆螺旋端面上的节圆O1作定圆，另一螺杆螺旋的节圆O2作动圆，当动圆沿着定圆作顺时针纯滚动时，以动圆O2节圆上的b点为摆点的轨迹，即为普通外摆线ab。在坐标系XO1Y中建立其方程式为

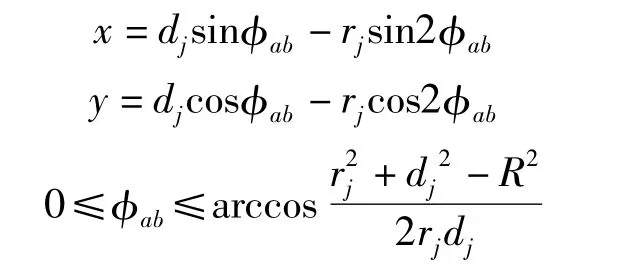
式中，rj为节圆半径;dj为两圆的中心距;R为齿顶圆半径;r为齿根圆半径;φab为齿形曲线ab的齿形转角，即型线起始位置b随着动圆滚动至终点位置a，此时两圆心连线O1O2和O1O2a之间的夹角。

1.2 长幅外摆线bc

以螺杆螺旋端面上的节圆O1作定圆，另一螺杆螺旋的节圆O2'作动圆，当动圆沿着定圆作逆时针纯滚动时，动圆外以O2'为圆心的螺旋齿顶圆上的c点为摆点的轨迹，即为长幅外摆线bc。在坐标系XO1Y中建立其方程式为

式中，φbc为齿形曲线bc的齿形转角，即型线起始位置c随着动圆滚动至终点位置b，此时两圆心连线O1O2'和O1O'2a之间的夹角;θbc为伸长外摆线bc的极角。

2 双头螺杆的端面型线

双头双螺杆泵螺杆齿形端面型线如图2所示。齿形的端面型线是由12段曲线连接而成，其分别是 ab、bc、ad、de、ef、fg、gh、hi、il、lk、kj和 jc。其中曲线 def和 abc关于直线 MON对称;jkl与ghi分别和abc与def关于直线AOB对称。其中各段齿形曲线性质见表1。

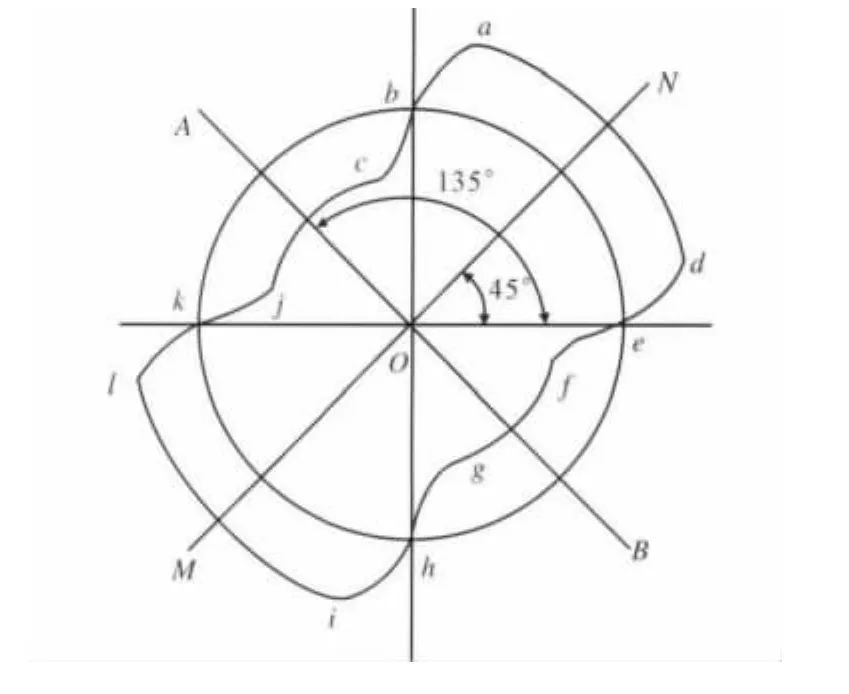
图2 双头双螺杆泵的端面型线Fig.2 Face type line of the double helix twin-screw pump

表1 主从螺杆端面齿形Tab.1 Toothed face of master-slave screw

由ab、bc段的型线方程，可以得出de、ef段的曲线方程和圆弧段ad和cj的曲线方程。

(1)de段。

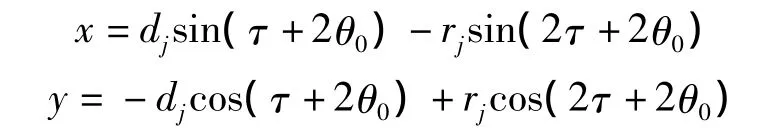
(2)ef段。

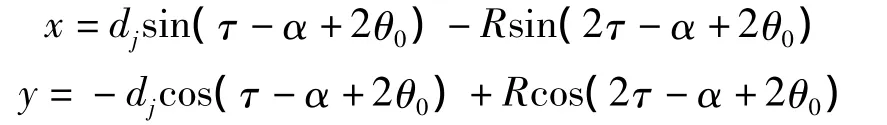
(3)ad段。

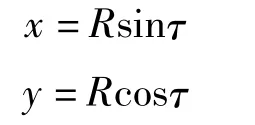
(4)cj段。

式中，τ 为变量;α =θbc;θ0=45°。

同理，可得lk、hi、kj、gh、fg、il各段曲线方程。

3 共轭型线方程

Ω型双螺杆泵最大的特点是一对螺杆依靠一对同步齿轮传递扭矩，两根螺杆有两对轴承支撑，因此螺杆的螺旋面之间可以实现互不接触。从齿形共轭的角度根据主动螺杆的型线方程推导得出从动螺杆的型线方程，转子的啮合对应关系如图3所示。

图3 原始型线和共轭型线Fig.3 Original profile and conjugate profile

［1］，当螺杆的发生圆为另一螺杆的节圆，且发生圆与另一螺杆螺旋节圆的圆心相同时，普通外摆线和长幅外摆线的共轭曲线已不再是曲线，而变成了一个点，即点成为共轭曲线为内摆线的特殊情况。根据坐标变换和包络原理，可得

主动螺杆上的ab段曲线对应的共轭曲线为从动螺杆上的b'(0，rj)点。

主动螺杆上的b(0，rj)点对应的共轭曲线为从动螺杆上的a'b'段曲线，其方程为

主动螺杆上的bc段曲线对应的共轭曲线为从动螺杆上的a'点。其坐标为

式中，θab为普通外摆线ab的极角，

主动螺杆上的 a(Rsinθab，Rcosθab)点对应的共轭曲线为从动螺杆上的b'c'段曲线，其方程为

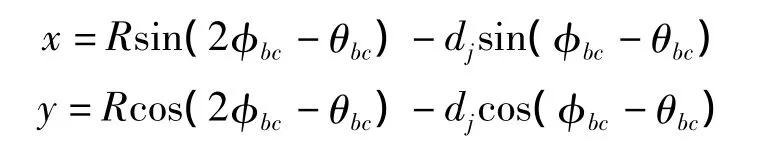
由此得出，从动螺杆和主动螺杆的齿形曲线轮廓是相同的。

4 基于Pro/E的双头螺杆泵虚拟建模

根据螺杆转子端面型线各段方程式，利用Pro/E的可变剖面扫描方法建立了双头双螺杆泵转子的三维模型，如图4所示。其中转子的相关参数为 rj=152.5 mm，dj=305 mm，R=200 mm，r=105 mm。

图4 双头双螺杆泵转子三维模型Fig.4 Three-dimensional model of the double helix twin-screw pump

5 螺杆转子的螺旋曲面方程

螺杆螺旋端面上的齿形曲线绕螺杆轴线旋转，并作轴向位移，两运动合成的轨迹就构成了螺旋面。

根据螺旋曲面的生成原理，可得其方程为

式中，T为螺旋导程;xm、ym为螺杆转子端面型线方程;θ为螺杆转子端面型线扭转角度参数;“±”为当主动转子右旋时取上面的符号，反之取下面的符号。

6 结论

本文分析了Ω型双头双螺杆泵转子型线的组成和形成原理，得出转子型线的数学模型，运用包络原理得出型线的共轭曲线方程式，推导得出共轭型线与原始型线的啮合对应关系。利用坐标变换得出转子端截面各段摆线的数学方程式，结合具体产品利用Pro/E对Ω型双头双螺杆泵转子进行三维建模，建立其螺旋曲面方程，为后续的双头双螺杆泵的性能研究和优化改进提供依据。

参考文献:

［1］李福天.螺杆泵［M］.北京:机械工业出版社，2010.

［2］李增亮，李风涛.双螺杆泵转子型线啮合特性分析［J］.石油机械，2009，37(6):28－32.

［3］李增亮，张瑞霞，高扬，等.双螺杆泵型线分析及仿真研究［J］.石油机械，2008，36(3):41－44.

［4］肖文生，万邦烈.双头双螺杆齿形型线啮合原理［J］.石油大学学报，1997，21(6):44－47.

［5］曹锋，邢子文，李新宏，等.一种双螺杆多相流混输泵型线的理论分析［J］.西安交通大学学报，1999，33(11):43－46.

［6］杜秀华，任斌，韩国有.双头单螺杆泵的线型设计及虚拟建模［J］.石油矿场机械，2007，35(1):33－35.

［7］陈金海，王丽霞，陈德伟.双螺杆泵型线的修正［J］.流体机械，2006，34(6):41－43.

［8］肖文生，张彦廷，万邦烈.一种单头双螺杆的啮合特征［J］.石油大学学报，1998，22(4):62－63.

［9］ANA MERCEDES MARTIN CEREIJO.Multiphase Twin－Screw pump Modaling forThe Oil and Gas Industry［D］.Texas A＆M University，2003.