半潜式航行体横滚调整方式分析

欧阳凌浩，师子锋

( 中国船舶重工集团公司 第七一〇研究所，湖北 宜昌443003)

1 概 述

随着技术的发展，反水雷逐渐转入无人系统，法国DCN 公司开发的“海上卫士”FDS3 遥控猎雷系统(如图1)就是此类反水雷装备。该系统是由加拿大ISE 公司开发的“海豚”半潜式航行体和水下拖曳系统组成，其中半潜式航行体类似于1 艘小型无人潜艇，航行于半潜状态，通过舰上遥控设备控制航行。它拖带1 个水下拖体，可避开航行体发出的噪声，其上携带多种声呐，可有效探测海底和海中目标。在探测过程中，航行体的姿态和航迹对探测精度影响较大。本文以该遥控猎雷系统中的“海豚”半潜式航行体作为原型，分析其调整横滚和航向的因素，确定控制方案。

“海豚”半潜航行器全长8.3 m，最大直径2.5 m，质量6 700 kg，航行器由柴油机推进，柴油机的吸气和排气孔以及通信天线伸出水面，它可以12 kn的航速航行400 n mile (740 km)。续航时间与拖体的深度和速度有关，大致在16 ～74 h 之间。“海豚”半潜式航行器采用260 kW Caterpillar 3116 涡轮增压船用柴油机作为动力，油箱容量726 kg，采用对转螺旋桨，最高航速达17.5 kn，拖曳航速达10 ～12 kn。

图1 FDS3 探测系统吊放入水状态Fig.1 State of hung into water

2 航行体六自由度运动方程组

2.1 坐标系

建立航行体空间运动方程组主要用到体坐标系oxyz 和地面坐标系ox0y0z0两种坐标系。体坐标系oxyz的原点位于航行体浮心所在横截面与航行体轴线的交点，x 轴沿航行体轴线指向航行体头部;y 轴位于航行体纵对称面内垂直x 轴，指向上方;z 轴垂直oxy平面，按右手法则指向侧向。地面坐标系ox0y0z0的原点取初始时刻航行体体坐标系的原点在水平面上的投影点;ox0轴沿航行体的纵对称面与水平面的交线，指向前方;oy0轴铅垂向上;oz0轴按右手规则。

体坐标系用于建立航行体动力学方程，地面坐标系主要用于确定几何参数。地面坐标系和体坐标系之间的夹角确定了航行体的3 个姿态角，即俯仰角θ、偏航角ψ 及横滚角φ，体坐标系原点在地面坐标系中的3 个坐标:x0，y0，z0确定了航行体的空间位置。

地面坐标系到体坐标系的转换矩阵为

体坐标系到地面坐标系的转换矩阵为

2.2 空间运动方程组

利用动量和动量矩定理可以在体坐标系中建立如下的航行体空间运动动力学方程组:

式中:各符号涵义见文献［3］。

航行体转动角速度(ωx，ωy，ωz)与3 个姿态角变化率之间的运动学关系式由下式描述:

航行体的空间位置由下式确定:

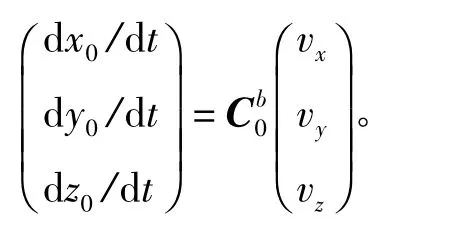
攻角α、侧滑角β 及速度v 的定义式为

弹道角θc，ψc，φc和姿态角θ，ψ，φ 及攻角α、侧滑角β 之间的几何关系式为

上述各式构成了航行体空间运动方程组，含有vx，vy，vz;ωx，ωy，ωz;θ，ψ，φ;θc，ψc，φc;x0，y0，z0;α，β，v 共18 个未知量。

3 仿真初始条件

由于“海豚”半潜式航行器使用柴油机作为动力，需采用桅杆结构进行进排气。考虑桅杆高度，半潜式航行器的航行深度不得大于4 m。初始深度2 m，取航行深度2.5 ～4 m，每0.5 m 一个计算状态。取航行速度8 ～16 kn，每4 kn 一个计算状态。共12 个仿真工况。初始姿态角、流体动力角均为0，前水平舵角为平衡舵角。海流大小3 kn，方向正侧向。

3.1 后水平舵差动调整航行体横滚

3.1.1 仿真工况与初始条件

表1 后水平舵差动调整航行体横滚仿真工况Tab.1 The simulation conditions of using diving rudder after to adjust the roll of the vehicle

3.1.2 控制方法

舵功能分配:前水平舵用于平衡，后水平舵用于深度与横滚控制，后垂直舵用于航向控制。

控制方程:

深度δhh=Kyy+Kθθ+Kωzωz;

航向δv=Kzz+Kψψ+Kωyωy;

横滚δd=Kφφ+Kφxωx。

3.1.3 仿真结果

图2 ～图5 分别给出了航行体航速8 ～16 kn 速度下姿态及航线的变化曲线。

由仿真曲线可见:航行体可以实现定常水平直线运动3 通道耦合控制，航线控制精度与随着航速的增加而增加，8 kn 航速下，稳态航线与预定航线侧偏约0.5 m，16 kn 航速时，侧偏为0.22 m;航行体俯仰和横滚角度均可以达到0°左右，航行体首偏角度随着速度的增加而减小。

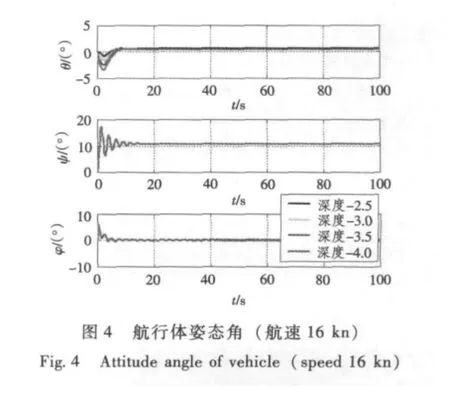
图5 航行体偏航距离(航速16 kn)Fig.5 Yaw distance of vehicle (speed 16 kn)

3.2 垂直舵差动调整航行体横滚

3.2.1 仿真工况与初始条件

表2 垂直舵差动调整航行体横滚仿真工况Tab.2 The simulation conditions of using vertical rudder after to adjust the roll of the vehicle

3.2.2 控制方法

舵功能分配:前水平舵用于平衡，后水平舵用于定深控制，后垂直舵用于航向与横滚控制。

控制方程:

深度δhh=Kyy+Kθθ+Kωzωz;

航向δv=Kzz+Kψψ+Kωyωy;

横滚δd=Kφφ+Kφxωx。

3.2.3 仿真结果

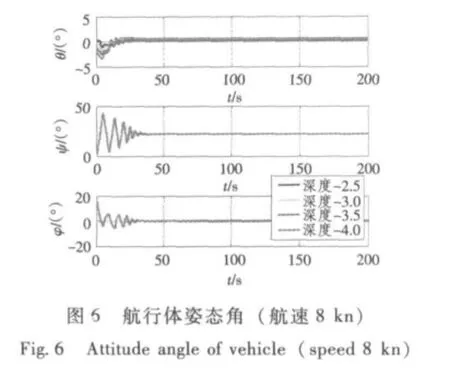
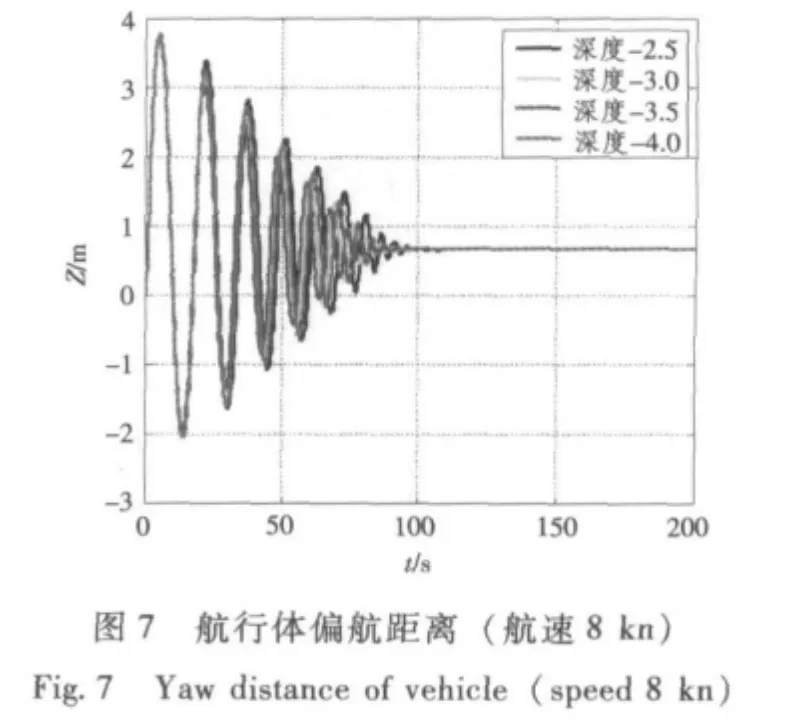
图6 ～图9 分别给出了航行体航速8 ～16 kn 速度下姿态及航线的变化曲线。

由仿真曲线可见:航行深度对航行体姿态影响不大，只是过渡时间略有差别，航行体的俯仰和横滚均可以达到0°左右，其首偏角度随着航行体速度增加而减小;航行体航迹控制精度随着航速的增加而增加，8 kn 航速下，稳态航线与预定航线侧偏约0.7 m，16 kn 航速时，侧偏为0.32 m。

4 结 语

本文对不同航行深度和不同航行速度下的航行体运动进行仿真分析，由结果可知:水平舵差动和垂直舵差动对航行体姿态控制精度影响不大，航行深度对航行体姿态及航迹偏差最终结果影响较小，只是其过渡时间有所差别。垂直舵差动调整航行体横滚时会导致航行体航迹偏差增大，因此建议采用水平舵差动方式来调整航行体横滚，垂直舵只做航向控制。

［1］李天森.鱼雷操纵性［M］.北京:国防工业出版，1999.

LI Tian-sen.Torpedo manoeuvrability［M］.Beijing:National Defense Industry Press，1999.

［2］黄景泉，张宇文.鱼雷流体力学［M］.西安:西北工业大学出版社，1989.

HUANG Jing-quan，ZHANG Yu-wen.Torpedo hydrodynamics［M］.Xi′an:Northwestern Polytechnical University Press，1989.

［3］严卫生.鱼雷航行力学［M］.西安:西北工业大学出版社，2005.

YAN Wei-sheng.Torpedo mechanics［M］.Xi′ an:Northwestern Polytechnical University Press，2005.

［4］李光泉.自动控制原理［M］.北京:机械工业出版社，1990.

LI Guang-quan.Principle of automatic control［M］.Beijing:Machinery Industry Press，1990.

［5］李天森，马惠，李斌，等.水下运动体横-滚控制弹道稳定性探讨［J］.船舶力学，2004，8(2):42-46.

LI Tian-sen，MA Hui，LI Bin，et al.Study on the stability of transverse-rolling-controlled trajectory of submerged bodies［J］.Journal of Ship Mechanics，2004，8(2):42-46.

［6］杜晓旭，潘光，等.低速水下航行器横向-横滚操纵性研究［J］.弹箭与制导学报，2005，25(3):581-583.

DU Xiao-xu，PAN Guang，et al.Study on maneuverability of AUV′s transverse-roll motion［J］.Journal of Projectiles Rockets Missiles and Guidance，2005，25(3):581-583.