“溶解热测定”实验数据处理的双倒数模型

王 曦，曾 馨，韩 翔，张业中，吴爱斌 （长江大学化学与环境工程学院，湖北荆州434023）

“溶解热测定”是物理化学中的一个经典实验，其实验原理是采用电热补偿法来测定硝酸钾在水中的积分溶解热Qs，其他3种热效应 （微分稀释热、微分溶解热和积分稀释热）则可通过Qs～n0（n0＝nH2O／nKNO3；nH2O、nKNO3分别为水和硝酸钾物质的量）曲线求得。学生在实验数据处理时需要先做Qs～n0图，再做某些点的切线来求算微分溶解热，若学生运用图解法［1］作图，则会使数据处理步骤变得十分繁琐，并且作图效果差，给实验结果带入了较大的人为误差。故教学中通常要求学生选取合适的数学模型并借助Origin软件［2－7］对实验数据进行拟合，得出相应的Qs～n0解析式，再根据解析式求得Qs对n0的导数Q′s，代入相应的n0值，可求得该点处的斜率，即得到不同n0的微分冲淡热，由点（n0，Qs）和该点处的斜率可求出唯一的直线方程，进而得到所求得的截距，即微分溶解热。常见的数学模型有对数模型［8］、多项式模型［9］、一次指数衰减模型［10］：

然而这些模型未能完全反映硝酸钾溶解时的一些特征，物质溶解是溶质的微粒 （分子或离子）离开固体 （液体）表面扩散到溶剂中以及溶质的微粒 （分子或离子）和溶剂分子生成溶剂化物的过程。前一过程是吸热过程，后一过程放热过程。对不同的溶质来说，吸收的热量和放出的热量并不相等，故不同物质溶解表现出吸热或放热现象。硝酸钾溶解时，因为它和水分子的结合不稳定，吸收的热量比放出的热量多，就表现为吸热，在溶解时，溶液的温度就降低。

对于硝酸钾溶解热测定实验，结合实验事实及相关文献，硝酸钾溶解时有以下特征：①当溶剂量趋于无穷大，即n0趋于无穷大时，Qs为一常数［11］；②由实验数据作图可观测到，随着n0的增大曲线斜率逐渐变小；③当n0等于零，即溶剂（水）不存在时，硝酸钾不存在微粒扩散以及微粒溶剂化作用，由此得出当n0等于零时，Qs也应为零。

为此，笔者根据以上特征提出了双倒数模型1／Qs＝A／n0＋B。

1 热测定实验步骤及数据

该实验使用南京桑力电子设备厂生产的SWC－RJ溶解热测定装置，实验步骤如下：①在电子天平上依次称取8份质量为2.5，1.5，2.5，3.0，3.5，4.0，4.0，4.5g的硝酸钾 （应预先研磨并烘干），记下准确数据并编号。②在台式天平上称取216.2g蒸馏水于杜瓦瓶内，放入磁珠，拧紧瓶盖并放到反应架固定架上。③将O型圈套入传感器，调节O型圈使传感器浸入蒸馏水约100mm，把传感器探头插入杜瓦瓶内。④按下 “状态转换”键使仪器处于测试状态。调节 “加热功率调节”旋钮，使功率P＝2.5W左右。调节 “调速”旋钮使搅拌磁珠为实验所需要的转速。⑤实验时，先让加热器正常加热，使温度高于环境温度0.5℃左右，按 “温差采零”键，仪器自动清零，立刻打开杜瓦瓶的加料口，按编号加入第1份样品并同步计时，观察温度变化，等温差回到零时，加入第2份样品，以此类推，加完所有的样品。⑥实验结束，按 “状态转换”键，使仪器处于“待机状态”。将 “加热功率调节”旋钮和 “调速”旋钮左旋到底，关闭电源开关，拆去实验装置。实验数据记录见表1。

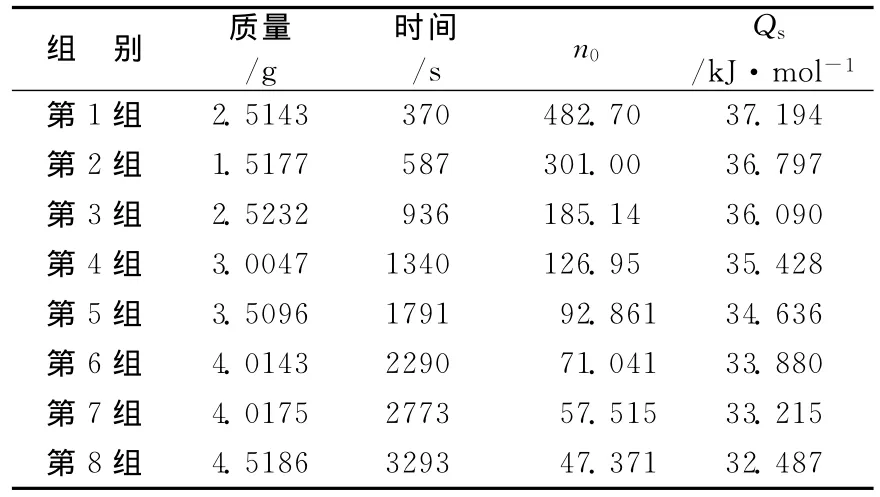
表1 硝酸钾溶解热的实验数据

2 数据拟合及讨论

通过Origin7.5软件对表1数据进行处理，对Qs，n0分别进行对数模型拟合、多项式模型拟合、一次指数衰减模型拟合和双倒数模型拟合，各种模型Origin拟合图如图1所示。

从图1可看出，指数衰减模型、对数模型拟合所用参数均为3个，其拟合相关系数均比双倒数模型拟合的相关系数要低，说明这2种模型的拟合准确度均没有双倒数模型拟合的准确度高。且当n0趋于零时，对数模型与指数衰减模型的Qs均不为零，不符合前述特征③：“当n0等于零时，Qs也为零”；在n0趋于无穷大时，对数模型的Qs为无穷大，不符合前述特征①：“当n0趋于无穷大时，Qs为一常数”。

从图1中还可看出，多项式模型的拟合相关系数最大，但多项式模型拟合所用参数最多 （4个），其高拟合精度是用更多的待定参数而达到的，拟合步骤较多，Qs～n0解析式较复杂，对后续数据处理不便，尤其对Origin软件初学者有一定难度。且多项式模型在n0趋于无穷大时，Qs为无穷大；当n0趋于零时，Qs不为零，不符合前述特征①与特征③。

而双倒数模型在形式上更简洁，所用参数只有2个，比上述3种模型的拟合参数都少，准确度也较高，且符合前述特征①、②和③。当n0＝200时，双倒数模型Qs＝36.25kJ／mol，结果与实验要求值Qs＝（35.00±2）kJ／mol符合较好。双倒数模型的线性化处理以及相对较少的待定参数，使应用该模型作图、分析更为方便，尤其相较于多项式模型。为验证双倒数模型的可行性，将双倒数模型对文献 ［12］已公布的数据进行了拟合，得1／Qs＝0.18559／n0＋0.02681（R2值为0.9940），当n0＝200时，双倒数模型Qs＝36.05kJ／mol比原文Qs＝36.17kJ／mol更接近实验准确值Qs＝35.00kJ／mol。

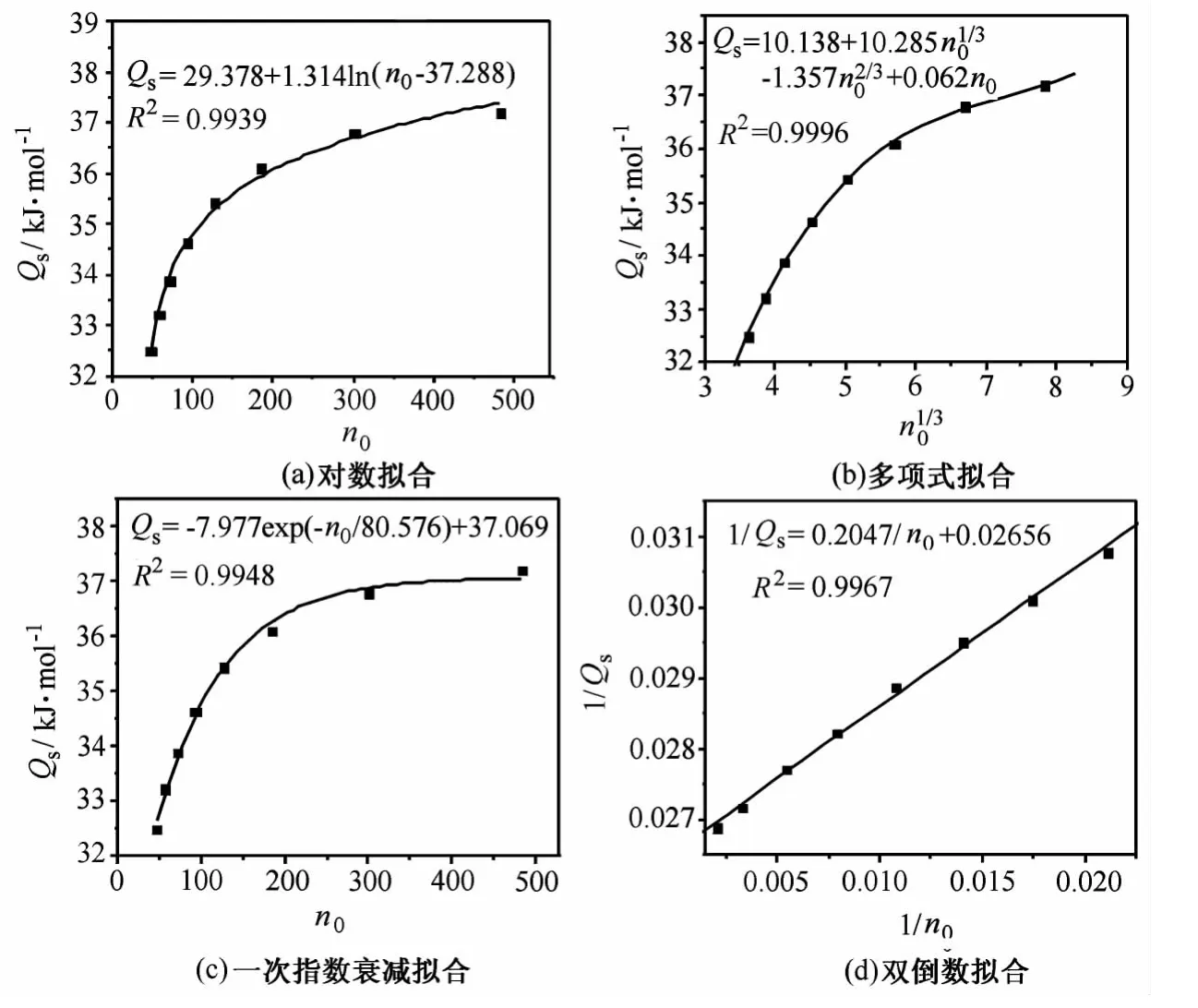
图1 Qs～n0关系曲线

3 结 语

一个好的数学模型应既能够与实验数据相接近，又能够反映一些实验事实。选取合适的数学模型进行拟合来确定Qs～n0解析式，可以有效减小数据处理中的人为误差，是一种行之有效的手段。在KNO3溶解热测定实验中，数据处理阶段应用何种数学模型更为适合尚无明确的结论。笔者系统地比较了用于处理KNO3溶解热测定实验数据的一些常见数学模型，提出了更适合学生运用、形式简洁、参数更少、准确度较高的双倒数模型1／Qs＝A／n0＋B，方便了学生对该实验的数据处理。