一种改进的DY共轭梯度法及其全局收敛性
2013-12-01王安平长江大学工程技术学院基础教学部湖北荆州434020
王安平 (长江大学工程技术学院基础教学部,湖北 荆州434020)
马 烁 (荆州理工职业学院基础课部,湖北 荆州434000)
考虑无约束优化问题:

式中,f:Rn→R连续可微。共轭梯度法是求解该问题的一类有效算法。一般的共轭梯度法迭代公式为:
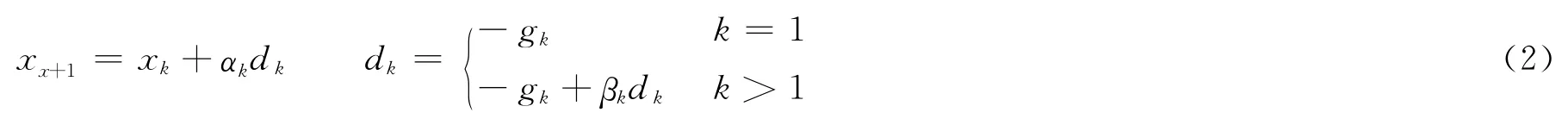
式中,x1为初始点;dk为搜索方向;αk是由某种线性搜索或由特定公式计算出的步长因子;βk为标量;g(x)= ▽f(x),gk= ▽f(xk)。共轭梯度法的关键是选取αk和βk,不同的αk和βk决定了不同的共轭梯度算法。常用选取αk的线搜索是标准Wolfe线搜索,即选取αk>0满足:
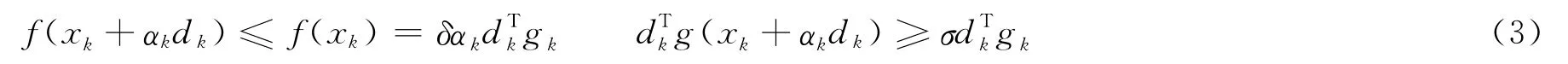
式中,δ和σ是满足0<δ<σ<1的常数。而βk的选取公式常用的有:
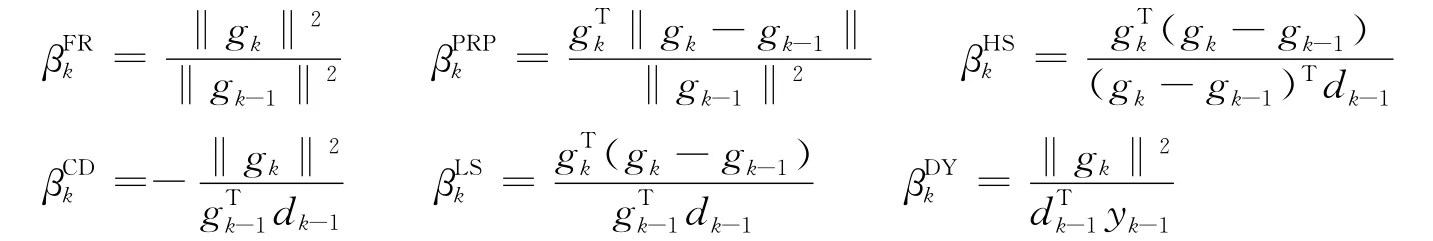
对应的共轭梯度法依次为FR方法[1]、PRP方法[2]、HS方法[3]、CD方法[4]、LS方法[5]和 DY 方法[6]。
在众多共轭梯度法中,为了保证下降方向,许多学者都做了深入的研究。文献 [7]提出了一种改进的DY共轭梯度法,参数βk的计算公式为:

受文献[7]的启发,笔者在MDY方法的基础上,给出了一个新的参数βk的取法,即:
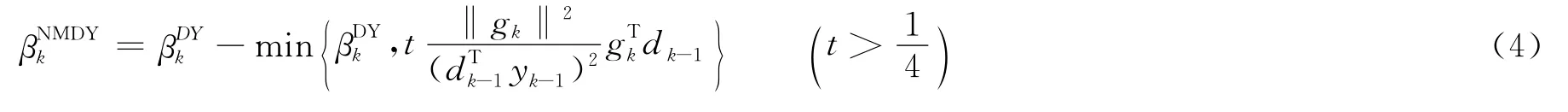
1 改进的DY算法及其充分下降性
改进的DY算法如下:
步1 给定初始点x1∈Rn,ε>0,d1=-g1,令k=1;
步2 若‖gk‖≤ε,则停止迭代;否则转入步3;
步3 由式(3)求得αk;
步4 计算xx+1=xk+αkdk,若 ‖gk+1‖ ≤ε,则算法停止,否则转步5;
步5 利用式(4)计算βk+1。计算dk+1=-gk+1+βk+1dk,置k=k+1,转步2。
定理1 设迭代方向由:


证明 当k=0时,dT0g0=-‖g0‖2,结论成立。
当k≥0时,dk=-gk+βNMDYkdk-1两边与gk做内积:
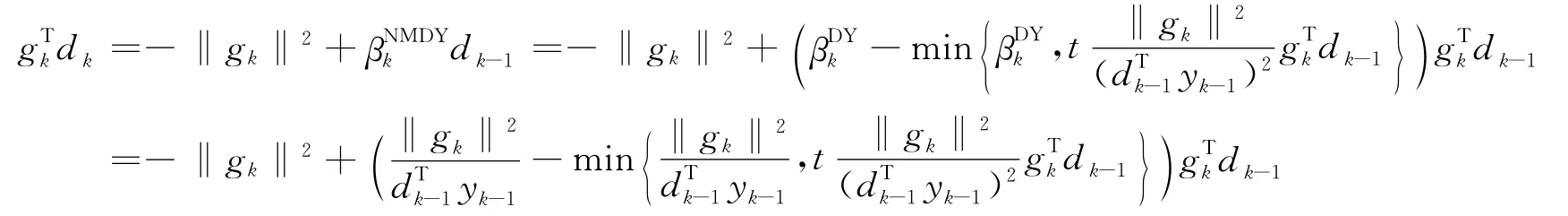
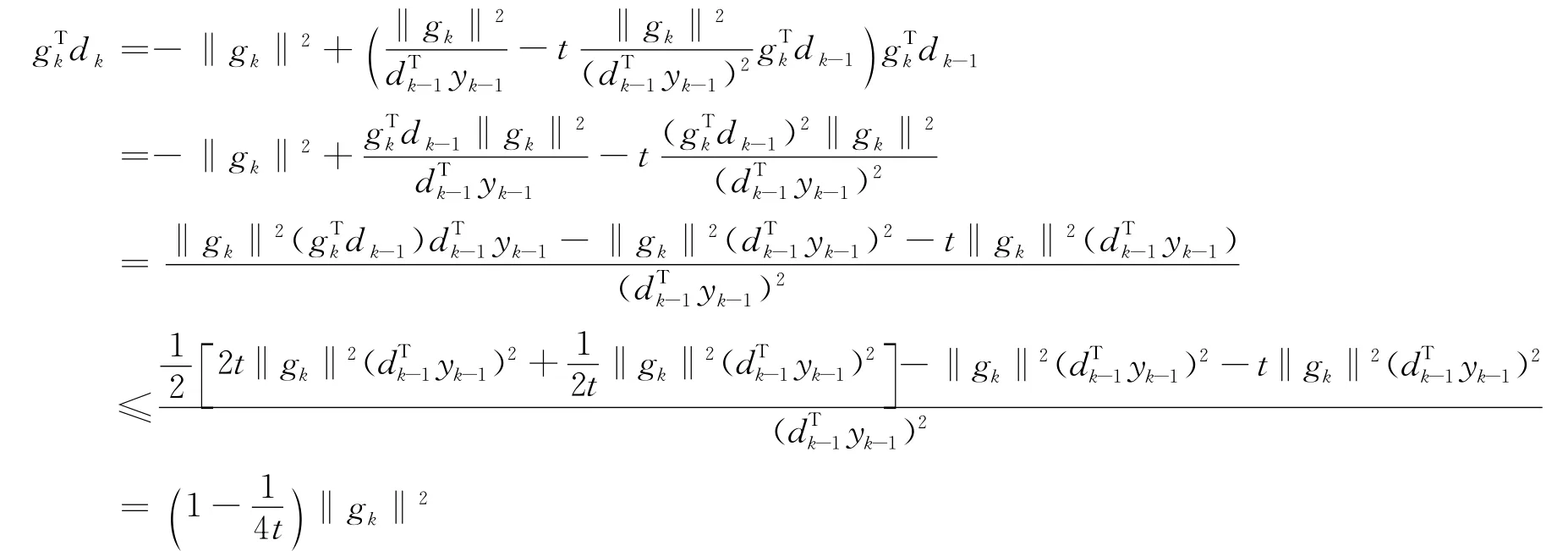
2 算法的全局收敛性
下面笔者将在一定的假设条件下证明NMDY算法的全局收敛性。假设条件(A)如下:
(1)水平集L1= {x∈Rn|f(x)≤f(x1)}有界,其中x1为初始点;
(2)在水平集L1的一个邻域U内,f(x)是连续可微的,其梯度g(x)是lipschitz连续的,即存在常数L>0使:
‖g(x)-g(y)‖ ≤L‖x-y‖ ∀x,y∈U引理1 设目标函数f(x)满足假设A,序列{xk}由式(2)产生,其中βk由(4)计算,αk满足式(3),则。此关系式称为Zoutendijk条件。
证明 由定理1及式(3),则有:
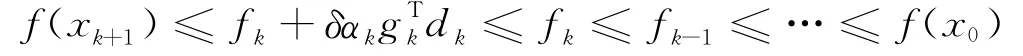
则式(6)说明了函数列{fk}有界。再由定理1及式(3)和假设条件(A)中的第2个条件,则有:

再联合式(3)可以得到:
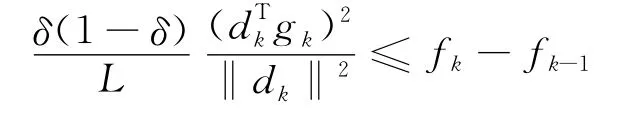
又因为函数列{fk}有界,所以有:
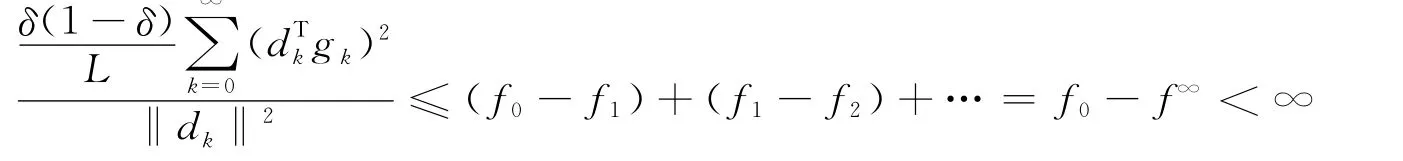
定理2 设目标函数f(x)满足假设条件A,序列{xk}由式(2)产生,其中βk由式(4)计算,αk由式(3)确定。假设存在一个正数α*,满足αk≥α*,则有:

证明 由假设A中的(1),则存在一个常数M>0使得:

由式(8)和αk≥α*,可以得到:

由式(9)及引理1和定理1的结论,可以得到式(7),即定理2得证。
