大地电磁反演中改进的自适应正则化因子选取

向 阳，于 鹏，陈 晓，唐 睿

（同济大学 海洋地质国家重点实验室，上海200092）

如何解决反演过程受初始模型影响的局限并提高解的稳定性，一直是地球物理反演的关键问题．吉洪诺夫正则化方法［1］已被广泛接受和应用于解决这种不适定性反问题．正则化反演通过在目标函数中加入模型约束，进而降低反演的多解性．正则化因子是数据拟合泛函和模型稳定泛函之间的折衷系数，正则化因子过大表示强调模型约束，数据总体是欠拟合的［2］；正则化因子过小表示反演主要拟合数据，反演结果容易受到数据噪音的影响产生虚假构造，总体是过拟合的，因此正则化因子的选取直接影响到反演结果［3］．如何选择合适的正则化因子，使反演既满足观测数据的充分拟合，同时还能保证模型的稳定性，一直是正则化反演中研究的热点，许多学者对此进行了深入研究．

前人研究较多的是经验定值方法．其中包括无偏风险估计预测方法［4－5］，该方法能给出估计值和真值之间的无偏的误差估计，但需要已知数据的噪音方差，而广义交叉验证方法［6－9］，则不需要估计数据的噪音方差便可进行计算，因此应用更为广泛．Hansen等［10－11］提出了L曲线法，选取L曲线拐点对应的值为最佳正则化因子，但需要进行多次试算才能得到一个最佳选择，且这个最佳也不是一个严格的取值，是一个相对的最佳［12］．

为了避免上述方法计算费时的问题，出现了许多正则化因子随反演过程可自适应调整的算法．在Occam 反演中［13－14］选取逼近数据拟合期望的最大的正则化因子为每次迭代的选择，该方法在每次反演计算中需额外正演多次，运算量较大．吴小平等［15］提出一种给定正则化因子初值，每次迭代直接按照衰减因子进行自适应调整的方法，但反演结果受正则化因子初值和衰减因子的选值影响很大．Zhdanov等［16－17］提出一种正则化因子呈阶梯状下降的自适应方法，选取数据拟合泛函和模型稳定泛函的比值为正则化因子初值，并选取经验性的衰减因子，在数据拟合效率下降时对当前正则化因子进行调整，具有较高的反演精度和计算效率．陈小斌等［18］提出一种完全自适应方案（CMD 方案），选取数据拟合泛函与模型稳定泛函的比值为每次迭代反演的正则化因子，该方案在整个迭代反演过程中始终强调数据拟合和模型稳定的平衡，具有较高稳定性．

为能在保持反演稳定的基础上进一步提高计算效率，本文以共轭梯度法求解带光滑约束的MT 反问题为框架，引入了几种正则化方式，包括L 曲线法、Occam 自适应、CMD 自适应以及Zhdanov自适应算法，通过比较分析这些方法在不同初始模型条件下的反演情况，提出一种比较合理且在初始模型偏差较大时也能保证反演稳定的自适应正则化算法．

1 MT共轭梯度法光滑反演

Constable等［13］提出的Occam 反演是一种带平滑约束的非线性最小二乘反演，该方法主要寻找满足数据拟合的模型中令粗糙度极小的模型作为迭代结果，所得的反演结果比较光滑，对初始模型依赖较小，算法稳定性高．

反演的目标函数为［3］

式中：Pα（m）为参数泛函；α为正则化因子；m为待解模型；φ（m）为数据拟合泛函；S（m）为模型稳定泛函；离散形式下，Wd，Wm分别为数据和模型的加权矩阵；A为正演算子；d为观测数据；We为稳定泛函矩阵，此处为Occam反演中的粗糙化差分矩阵；e为防止分母为零的小值；mapr为先验信息．

由于共轭梯度法具有不用求解大型线性方程组并且收敛速度快等优点，本文采用共轭梯度法代替文献［14］中的牛顿法求解模型参数，整个共轭梯度法的计算过程如下［3］：

式中：n为当前迭代次数；rn为数据拟合残差；A（mn），d分别为正演数据和观测数据；mn为模型参数；sn为模型稳定项；Wen为稳定泛函矩阵；αn为正则化因子为梯度方向；Fmn为偏导数矩阵为系数项为共轭梯度方向为步长．

本文反演计算中，迭代终止条件为数据拟合误差小于给定的阈值，若达不到此条件，则当迭代次数达到给定的最大次数时退出反演迭代．

2 模型试验

2．1 模型试验一

本文所采用的8 层层状模型与文献［18］中一致，在320～0．000 55Hz之间取40个计算频点，在正演响应数据上加入标准差为5%的随机噪音．反演模型为41层，纵向上从0．01km 到100km 按对数等间距剖分，反演迭代的拟合阈值为5%，即与所加入的噪音等级一致．反演中选取Bostick反演结果为先验信息．

2．1．1 多种正则化因子选取方法在不同初始模型下的反演结果

实际资料计算中，初始模型是不容易选择的，故作者选择了电阻率分别为1，10，100，1000，10 000 Ω·m的5个跨度比较大的均匀背景为初始模型来检验各种正则化反演方法的稳定性．为了直观地表现不同正则化因子选取方式对反演结果的影响，本文列出了不同初始模型条件下各方法的反演结果（图1），包括无正则化反演，L 曲线正则化反演，Occam 自适应正则化反演，CMD 自适应正则化反演，Zhdanov自适应正则化反演．因篇幅所限，各种正则化反演的流程以及参数选择参见文献［18－20］．需要指出的是，由L 曲线法计算后确定的正则化因子为0．1，Zhdanov自适应算法的衰减因子取0．9．

从图1可以看出，无正则化（图1a）和L 曲线法（图1b）的反演结果受初始模型的影响较大，只有在初始模型与实际模型偏差较小时才能得到较为理想的结果，当初始模型偏差较大时，反演结果很不稳定．Occam 自适应反演结果（图1c）受初始模型影响也很大，这主要是由于该方法虽然给定了很大的正则化因子为初值，但在迭代初期选择使拟合误差下降最快的正则化因子，正则化因子衰减很快，当初始模型偏离较大时，模型稳定泛函发挥的作用不够，故所得反演结果不理想．CMD 方案的反演结果（图1d）受初始模型影响相对较小，但由于正则化因子在计算中变化范围较小，最终的数据拟合精度不够，在较浅和较深区域的反演结果受初始模型的影响较大．Zhdanov自适应方法在不同的初始模型下所得到的反演结果（图1e）总体来说比较理想，但不同初始模型反演结果的一致性还不强，作者认为这主要是因为正则化因子的初始值在初始模型偏离较大时还是相对偏小．自适应正则化的方法在初始模型偏离较小时可以得到与传统定值方法相当的反演结果，且在实际操作中更加便捷，总体来说它们对初始模型的依赖性要小于定值的方法．

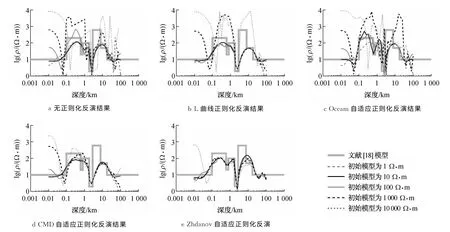
图1 不同初始模型下的不同正则化反演方法的反演结果Fig．1 Inversion results of different regularized methods by different initial models

2．1．2 本文改进的自适应正则化因子选取方法的反演结果

作者认为一种行之有效的正则化因子选取方案应该充分发挥模型稳定泛函的约束作用，以减小反演结果对初始模型的依赖性．针对初始模型偏离较大或初始模型不易选择的情况，结合上述模型试验结果，作者以Zhdanov自适应算法［3］为基本框架，提出了一种改进的自适应正则化方案．

在Zhdanov自适应算法中，选取数据拟合泛函和模型稳定泛函的比值为初始值，作者认为在初始模型m1偏差较大时，这样选取的正则化因子初值是偏小的，不能较好地发挥模型稳定的约束效果，应该选取更大的正则化因子α1为初值以增大模型稳定泛函的作用，使其在初始模型偏离真值较大时也能充分稳定，即在反演迭代的初期，充分发挥先验信息的约束作用，而在反演迭代的后期，随着正则化因子的减小进一步突出数据拟合的作用，得到一个较为精确的解．基于此，作者将这一比值乘以一个倍数k予以放大

Zhdanov自适应正则化反演算法中，当数据拟合效率下降时，即迭代前后数据拟合相对变化量Δφ＝（‖Wdrn‖2－‖Wdrn＋1‖2）／‖Wdrn‖2很小时，则按照一定的衰减因子q对当前的正则化因子进行调整，Zhdanov指出衰减因子q的经验取值区间为［0．5，0．9］，但并没有提出明确的衰减机制．基于此，作者试图寻找一种可以兼顾反演稳定性和计算效率的衰减机制．

作者同样按照Δφ来衡量反演过程的迭代效率，并将迭代效率分为3种情况，低效率，高效率和过渡阶段，在不同阶段，选取不同的衰减方案．在满足式4（a）时，数据拟合下降缓慢，说明当前的正则化因子不再适应当前的反演迭代，应选择一个较小的衰减因子来提高反演精度；在满足式4（b）时，数据拟合下降较快，应选择一个较大的衰减因子来保持反演稳定性；在满足式4（c）时，数据拟合下降一般，为了兼顾反演精度和稳定性，作者选取［ql，0．9］这一衰减区间．

作者设计了6种参数组合，选择电阻率分别为1，10，100，1 000，10 000Ω·m 的均匀背景为初始模型，反演结果和正则化因子迭代曲线见图2．结合图1e、图2，可以看出随着正则化因子初值以及衰减因子的增大，反演的一致性逐渐变强，反演结果对初始模型的依赖性逐渐变小．这也验证了作者对Zhdanov自适应正则化反演结果（图1e）跳跃的分析：直接选择数据拟合泛函和模型稳定泛函的比值为正则化因子初值在初始模型偏差较大的情况下是偏小的．在k取5，10，100时，即使衰减因子较小（图2b，2d，2f），模型稳定泛函的约束作用还是可以得到较好发挥，这说明通过增大正则化因子初值使稳定泛函在反演初期发挥较大贡献，可以减小反演结果对初始模型的依赖性．此外，在正则化因子初值相同的情况下，选择较大的衰减因子（图2c，2e），可以在反演过程中保持模型稳定泛函的约束作用，反演结果的一致性优于选择较小的衰减因子时的方案．

图2 不同初始模型不同自适应正则化因子选取方案的反演结果Fig．2 Inversion results with different adaptive regularization parameters by different initial models

此外，作者统计了k＝10，ql分别取0．4，0．5，0．6，0．7，0．8，0．9时的反演迭代次数、数据拟合误差和模型逼近误差，见图3，同样选择电阻率分别为1，10，100，1 000，10 000Ω·m 的均匀背景为初始模型进行反演，数据拟合和模型逼近均用相对均方根误差来统计．从图3a可以看出，随着正则因子初值和衰减因子的增大，反演达到阈值所需的迭代次数随之增多．分析图3b，3c，可以看出，ql取0．4时数据拟合和模型逼近情况跳跃最大，说明稳定性有待提高；ql取0．9时数据拟合和模型逼近跳跃较小，说明稳定性较高，但迭代次数较多，迭代效率不高；综合考虑以上因素，作者认为ql取0．5～0．8时本模型的反演可以兼顾模型稳定性和反演精度．

图3 不同初始模型不同自适应正则化因子选取方案的迭代次数、数据拟合和模型逼近统计Fig．3 Statistical graph of iterative number，data misfit and model approximation with different adaptive regularization parameters with different initial models

2．2 模型试验二

为了验证本文改进的自适应算法在复杂模型条件下的适应性，作者设计了如图4a所示的二维模型．采用k＝10，ql＝0．6，qh＝1．0参数组合对该模型进行了电场极化模式反演，初始模型分别为100 和10 000Ω·m 两种方案，反演结果见图4b，4c，此外，还进行了Zhdanov自适应正则化反演（图4d，4e）和正则化因子取定值0．1时的正则化反演（图4f，4g）予以对比．

图4 不同初始模型下的不同正则化方法的反演结果Fig．4 Inversion results of different regularized methods by different initial models

本文改进的自适应算法在两种初始模型条件下的模型逼近误差分别为0．208和0．206，可见初始模型对反演结果影响很小，所得反演结果一致性很高；Zhdanov自适应算法在两种初始模型条件下的模型逼近分别为0．217和0．397，所得反演结果一致性一般，在初始模型为10 000Ω·m 时，个别测点的反演已经出现不稳定的情况，跳越较大；正则化因子取定值0．1时正则化反演在两种初始模型条件下的模型逼近分别为0．211 和1．285，所得反演结果差异很大，初始模型为10 000Ω·m 时，已不能反演地下真实的电阻率分布，偏差很大，这也说明了经验定值法的局限性．可见本文改进的自适应算法在复杂模型条件下依旧可以保持反演的稳定性，对初始模型依赖小，而且可以保持较高的反演精度．

3 结论

正则化因子的选择决定着正则化反演的结果，如何选择合适的正则化因子一直是反演研究中的重点和热点．本文通过比较多种正则化因子的选取方法，分析了各种方法在给定不同初始模型条件下的表现，提出了一种改进的自适应正则化方法，得到了以下结论：

（1）本文提出的改进的自适应正则化方法，通过选择较大正则化因子初值和自动控制衰减因子，相比其他几种自适应正则化算法对初始模型的依赖小，可在不同初始模型的条件下得到精度及稳定性都很高的解，具有明显的优越性．

（2）本文提出的自适应正则化方案是基于共轭梯度法求解的光滑反演，但可推广至其他地球物理反演方法以及高维反演．建议在不强调计算时间代价的情况下，应选择较大的正则化因子初值和衰减因子；在必须考虑计算效率的情况下，建议选择较大的正则化因子初值和较小衰减因子以兼顾反演的稳定性和计算效率．

［1］ Tikhonov A N．Regularization of incorrectly posed problem［M］．Dokl：Soviet Math，1963．

［2］ Oldenbury D，Li Yaoguo．Inversion for applied geophysics：a tutorial［J］．Near－surface Geophysics，2005，5：89．

［3］ Zhdanov M S．Geophysical inverse theory and regularization problems［M］．［S．l．］：Elsevier Science，2002．

［4］ Wahba G．Spline models for observational data ［M］．Philadelphia：SIAM，1990．

［5］ Lin Y Z，Wohlberg B．Application of the UPRE method to optimal parameter selection for large scale regularization problems［J］．Southwest symposium on Image Analysis and Interpretation，2008：89．

［6］ Wahba G．Practical approximate solutions to linear operator equations when the data are noisy ［J］．SIAM Journal on Numerical Analysis，1977，14（4）：651．

［7］ Golub G H，Heath M T，Wahba G．Generalized cross－validation as a method for choosing a good ridge parameter ［J］．Technometrics，1979，21：215．

［8］ Haber E，Oldenburg D．A GCV based method for nonlinear illposed problems［J］．Computational Geosciences，2000，4（1）：41．

［9］ Chung Julianne，Nagy G J．A weighted－GCV method for Lanczos－Hybrid regularization ［J］．Electronic Transactions on Numerical Analysis，2008，28：149．

［10］ Hansen P C，O’Leary D P．The use of the L－curve in the regularization of discrete ill－posed problems［J］．SIAM Journal on Numerical Analysis，1993，14（6）：1487．

［11］ Hansen P C．Regularization tools：a matlab package for analysis and solution of discrete ill－posed problems ［J］．Numerical Algorithm，1994，14（6）：1．

［12］ 吴小平，徐果明．利用共轭梯度方法的电阻率三维反演研究［J］．地球物理学报，2000，43（3）：420．WU Xiaoping，XU Guoming．Study on 3－D resistivity inversion using conjugate gradient method ［J］．Chinese Journal of Geophysics，2000，43（3）：420．

［13］ Constable S C，Parker R L，Constable C G．Occam’s inversion：a practical algorithm for generating smooth models from electromagnetic sounding data［J］．Geophysics，1987，52：289．

［14］ deGroot－Hedlin C，Constable S．Occam’s inversion to generate smooth two－dimensional models from magnetotelluric data［J］．Geophysics，1990，55（12）：1613．

［15］ 吴小平，徐果明．大地电磁数据的Occam 反演改进［J］．地球物理学报，1998，41（4）：547．WU Xiaoping，XU Guoming．Improvement of Occam’s inversion for MT data ［J］．Chinese Journal of Geophysics，1998，41（4）：547．

［16］ Kumar A，Wan L，Zhdanov M S．Regularization analysis of three－dimensional magnetotelluric inversion ［C］／／2007 SEG Annual Meeting． San Antonio： Society of Exploration Geophysicists，2007：2007－0482．

［17］ Gribenko A，Zhdanov M S．Rigorous 3D inversion of marine CSEM data based on the integral equation method ［J］．Geophysics，2007，72（2）：WA73．

［18］ 陈小斌，赵国泽，汤吉，等．大地电磁自适应正则化反演算法［J］．地球物理学报，2005，48（4）：937．CHEN Xiaobin，ZHAO Guoze，TANG Ji，et al．An adaptive regularized inversion algorithm for magnetotelluric data ［J］．Chinese Journal of Geophysics，2005，48（4）：937．

［19］ 陈晓，于鹏，张罗磊，等．大地电磁与地震正则化同步联合反演［J］．地震地质，2010，32（3）：402．CHEN Xiao，YU Peng，ZHANG Luolei，et al．Regularized synchronous joint inversion of MT and seismic data ［J］．Seismology and Geology，2010，32（3）：402．

［20］ 陈晓，于鹏，张罗磊，等．地震与大地电磁测深数据的自适应正则化同步联合反演［J］．地球物理学报，2011，54（10）：2673．CHEN Xiao，YU Peng，ZHANG Luolei，et al．Adaptive regularized synchronous joint inversion of MT and seismic data［J］．Chinese Journal of Geophysics，2011，54（10）：2673．