基于可调谐FP滤波器的光纤光栅波长解调算法研究*-
2013-11-28黄俊斌顾宏灿
唐 波 黄俊斌 顾宏灿 吴 晶
(海军工程大学兵器工程系 武汉 430033)
1 引言
光纤布拉格光栅(Fiber Bragg Grating,FBG)是一种能感测应变、温度、压力、磁场等多种物理参量的光无源器件,作为光电子研究领域的新兴技术,在近年来受到了广泛的关注和应用[1~2]。光纤光栅传感器属于波长调制型光纤传感器,它是通过对光纤内部写入的光栅反射或透射波长的光谱检测,实现对被测结构的应变和温度等量值的绝对测量。常用的信号解调方法有:边缘滤波法、匹配滤波法、可调谐滤波法、射频探测法、光栅啁啾法、CCD测量法、干涉解调法等[3]。
可调谐F-P滤波解调系统具有体积小、价格低、响应速度快、信噪比和分辨率高、稳定性好等优势,可用于动静态的同时测量,适用于分布式测量,是比较理想的解调方法[4]。因此本文在对可调谐F-P滤波解调法进行研究的基础上,优化质心寻峰算法,并比较线性插值和抛物线插值两种波长输出算法,结果表明后者的解调精度较高,复杂程度较低。
2 解调原理
基于可调谐F-P滤波器的光纤光栅波长解调系统的本质是采用可调谐F-P滤波器将波长的变化转化为时域中接收光强的变化[5]。宽带光源照射光纤光栅传感器阵列,阵列反射的光经过耦合器进入到可调谐F-P滤波器中。给F-P滤波器施加一个扫描电压,以改变F-P滤波器的腔长,使F-P滤波器透射光的波长发生改变,若F-P滤波器的透射波长与光纤光栅的反射波长相等,则探测器能探测到最大光强,记录此时信号峰值位置对应的扫描电压,根据F-P腔的λ-V关系,就可以得到光纤光栅的中心反射波长[6~7]。
然而大多数光滤波器在响应过程中呈非线性,这就导致了波长扫描无法实现真正的线性,且光滤波器对温度、使用年限和结构等参数都十分敏感,导致滤波器光谱的非线性将随时间而不断变化[8]。这样,F-P滤波器透射光谱的非线性响应及其漂移特性降低了滤波器的稳定性,影响了波长探测的精度,如果没有一个精确固定的参考,使用该系统获得的数据将随着时间或温度变化而变得不可靠,为此,构建如图1所示的解调系统,使用一个波长分布已知的带标记热稳定标准具模块来补偿滤波器光谱的非线性和漂移的影响,以获得更好的精确性[8]。
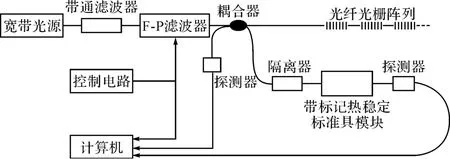
图1 解调系统原理图
3 解调算法
初始预设一个阈值,在阈值以上寻找起点和终点。从前往后逐点读取光纤光栅反射的信号或标准具的透射信号采集点,当前一个值小于阈值并且后一个值大于等于阈值时,采样点设为起始点;当前一个值大于阈值并且后一值小于等于阈值,采样点设为终点,循环操作,直至将所有点读取完毕。在寻找起点时,当前起点距离前一个终点的距离,以及在寻找终点时,当前终点距离前一个终点的距离均要大于200,因为设置波峰宽度范围,可以很好地屏蔽宽度远小于正常波的假波峰,提高解调精确度,降低其复杂程度。此外,在起点终点的判断语句中一定要有“>=”,因为假如没有“=”,则会出现恰好某点等于阈值,那么就不存在前一个小于而当前值大于的情况,于是我们在调试程序时就会发现截得的波峰会小于实际波峰的个数[10]。
经过波峰计算以后,标准具通道与传感通道的波峰位置将被计算出来。由于采用同一光源同时扫描,波峰位置与扫描电压对应关系一致,从而与可调谐滤波器输出光波波长对应关系也就一致。同时,标志通道的波长为已知量,那么就可以根据标准具通道的偏移位置与波长的对应关系计算出传感通道的光栅波长,下面分别运用线性插值和抛物线插值两种算法输出波长。
3.1 线性插值
根据可调谐F-P滤波器的输入信号,取光纤光栅传感器待解调信号和标准具校准信号数组进行波长解调运算,自动寻找光纤光栅传感器阵列反射信号和标准具透射信号的峰值位置,标准具透射信号的标记点处的位置间隔是其他峰值位置间隔的两倍(标记点与后波峰间隔为1.6nm,其余为0.8nm),据此识别标准具透射信号的标记点位置,根据标准具波长值列表确定标准具透射信号峰值位置对应的波长,光纤光栅传感器阵列反射信号的峰值位置在相邻的两个标准具透射信号峰值之间线性插值得出各光纤光栅传感器的工作波长,实现波长解调。假设某光纤光栅传感器的加权峰值位置x在标准具透射光加权峰值位置a和b之间,利用标准具的峰值波长列表确定峰值位置a、b对应的中心波长为λa、λb,则光纤光栅传感器的工作波长可由式(1)计算:
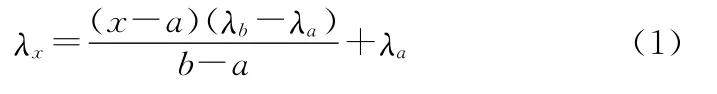
3.2 抛物线插值
抛物线插值与线性插值一样,要求所求曲线必须通过所有的点(xi,yi)。因此只有利用已知数据点的值,用插值方法来填补未知数据点的值。
三点抛物线插值:已知(xi,yi)(i=0,1,2)代入抛物线方程y=a+bx+cx2,联立方程:
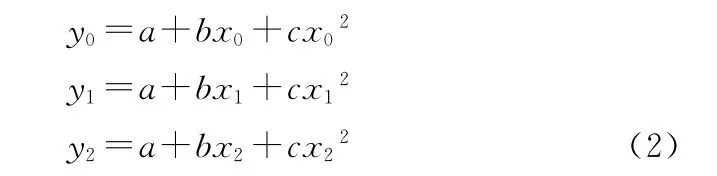
求出系数a,b,c后,再用所求的抛物线方程就可进行插值,从而输出波长,其中x为位置坐标,y为输出波长[11]。
4 实验结果
将光纤光栅传感器与波长解调仪相连,光栅自由放置。在没有外界信号作用的情况下,利用优化后的质心法寻找波峰,并通过线性插值和抛物线插值进行波长输出。
4.1 观察解调过程,比较系统稳定性
如图2所示为解调系统的质心法寻峰过程,细线部分为标准具光栅,粗线部分为光栅反射阵。
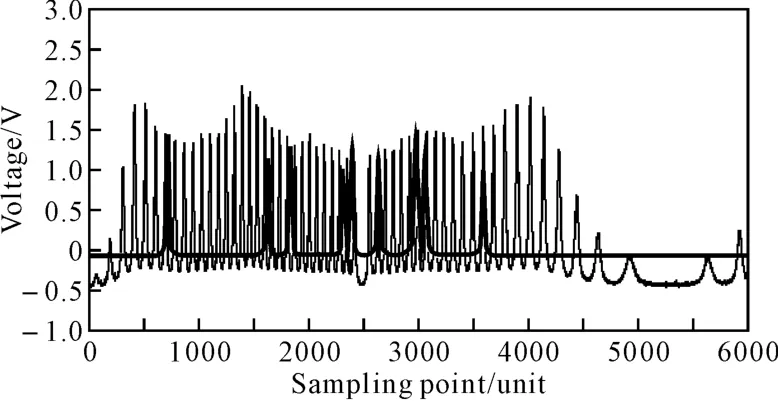
图2 光纤光栅反射阵列和标准具寻峰曲线
如图3所示为两种不同算法解调出来的波长输出曲线,均包含了八路信号的光栅反射波。
从寻峰曲线和波长输出曲线可以看出:程序解调过程均较为稳定,峰值位置找寻清晰,波长输出数据相对集中,抛物线插值算法波动较小,数据较集中。
4.2 比较系统各波长解调算法的标准差
在波长解调扫描频率为100Hz,采样频率为1.25MHz时,对实验后的数据进行处理,每组选取其中两路光栅信号,画出折线图,求出标准差。
图4为线性插值输出波长:
计算求得图4(a)组数据的解调程序输出的波长标准差为1.272pm,图4(b)组数据为1.302pm。
图5为抛物线插值输出波长:
计算求得图5(a)组数据解调程序输出的波长标准差为0.989pm,图5(b)组数据为0.814pm。

表1 两种算法的标准差对比
从表1中的数据可以看出,解调系统波长输出的标准差均控制在较小范围内,其中以抛物线插值算法标准差较小,表明抛物线插值算法所得数据较集中,结果误差较小。
4.3 改变系统初始设定值,找寻数值设定规律
改变阈值,观察程序波长输出变化,如图6所示,其中前半段阈值取为0.2nm,后半段阈值取为0.5nm。
从输出曲线可以看出:阈值改变后,波长输出的稳定程度发生明显变化,出现了明显的分界点。低阈值时数值相对集中,高阈值时数值则在较大范围内波动。
4.4 比较系统在大应变波长输出时的线性度
图7是在相同量程下进行大应变波长输出。
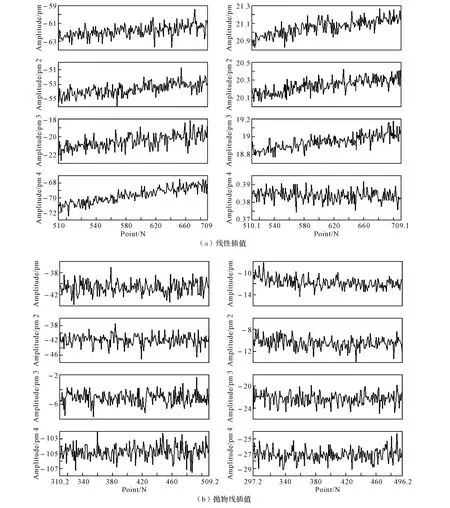
图3 解调系统波长输出
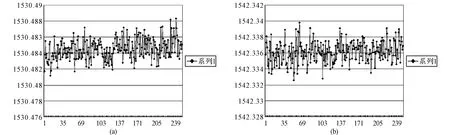
图4 线性插值输出波长
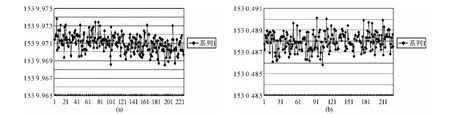
图5 抛物线插值输出波长
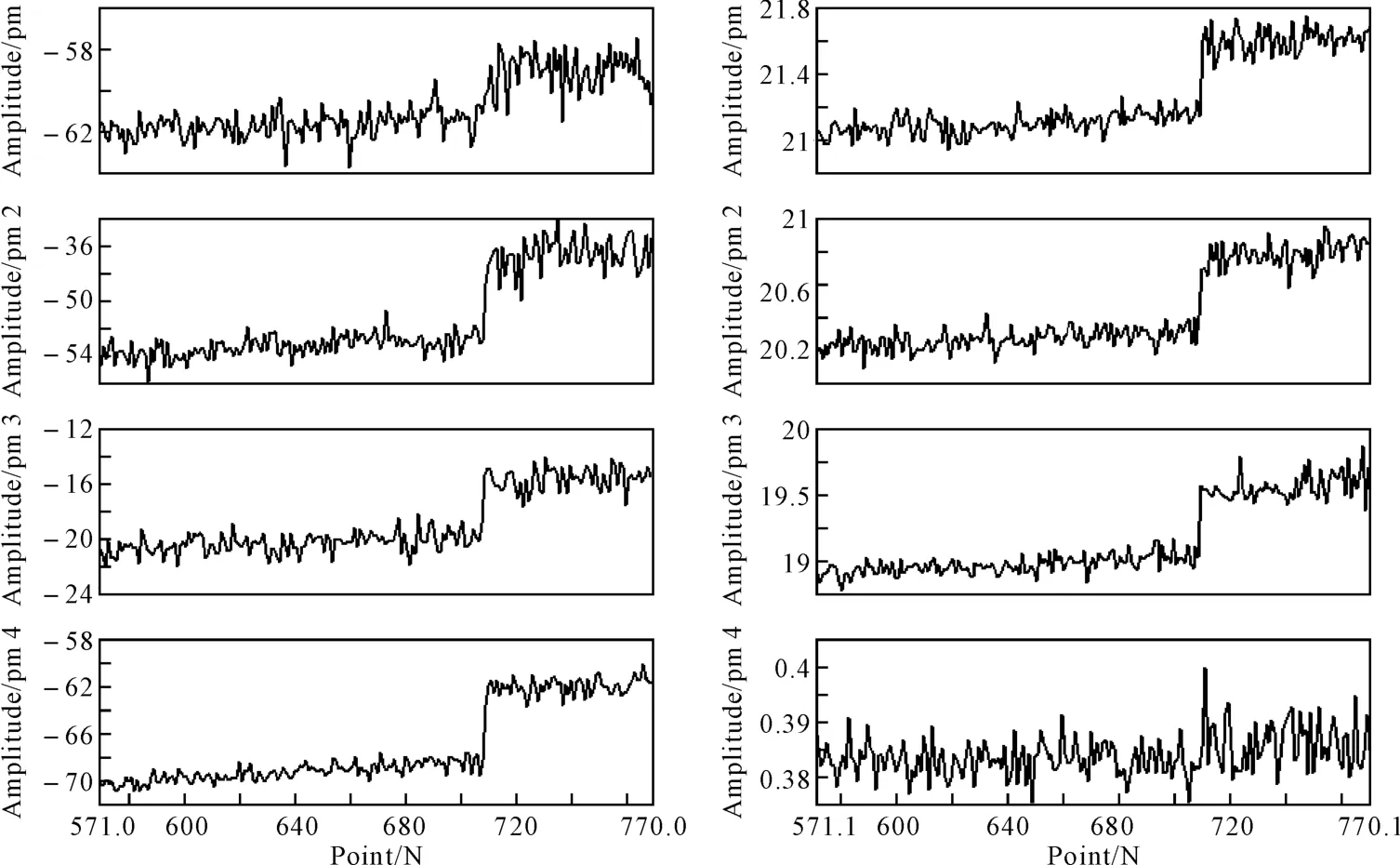
图6 阈值改变后的波长输出

图7 大应变波长输出
从图中可以明显看出,在相同量程下进行大应变波长输出时,抛物线插值的线性度要比线性插值好。
5 结语
使用优化后的质心法找寻波峰,再利用抛物线插值进行波长输出无论在精度和复杂程度上均占据明显优势。
[1]姜德生,何伟.光纤光栅传感器的应用概况[J].光电子·激光,2013,13(4):420-430.
[2]高璇,黄俊斌,顾红灿,等.基于光纤梳状滤波器的光纤Bragg光栅波长解调技术研究[J].舰船科学技术,2008,30(3):122-126.
[3]王涛.光纤布拉格光栅波长解调技术的研究[D].北京:北京交通大学,2009.
[4]KERSEY A D.Multiplexed Fiber Bragg Strain-sensor System with a Fiber F-P Wave-length Filter[J].Opt Lett,1993,18(16):1370-1372.
[5]江毅.高级光纤传感技术[M].北京:科学出版社,2009:239-240.
[6]赵勇.光纤光栅及其传感技术[M].北京:国防工业出版,2007:174.
[7]李川,张以谟,赵永贵,等.光纤光栅:原理、技术与传感应用[M].北京:科学出版社,2005:122-125.
[8]刘琨,刘铁根,江俊峰,等.基于FBG传感系统的可调光滤波器非线性研究[J].光电子·激光,2010,21(7):970-973.
[9]陈亮,黄俊斌,顾宏灿,等.一种实时校准的光纤Bragg光栅传感器解调系统[J].传感器与微系统,2005,28(7):89-91.
[10]张焘彦.基于可调谐滤波器和DSP的波长解调算法研究及软件设计[D].江苏:东南大学,2009.
[11]王霞,卫香莉,左占田.声波信号抛物线拟合与插值[J].石油仪器,2002,16(5):31-33.
