基于新型顺序约束的产品可靠性评估方法研究*
2013-11-28应新雅张志华
应新雅 张志华
(海军工程大学理学院 武汉 430033)
1 引言
产品的研制通常要经历设计样机、样机试验、发现问题并对样机进行改进、再试验、最后产品设计定型等多个阶段,在工程上通常将定型产品称为正样,将以前各阶段的产品称为样机。在产品研制过程中,通常积累有大量可靠性研制试验,并通过不断暴露产品设计存在的问题及改进设计,使产品可靠性稳步提高。如何有效利用产品研制阶段的可靠性研制信息,客观评估产品正样阶段的可靠性,并在充分利用可靠性研制试验信息基础上,组织开展产品可靠性鉴定试验,以减少产品可靠性鉴定试验量,解决传统可靠性鉴定试验量大,实施困难的问题,一直是可靠性统计研究领域的重要问题。
对于可靠性增长试验信息的处理问题,很多专家学者进行了大量研究工作,提出了多种可靠性增长试验信息处理方法。如文献[1]提出的AMSAA模型在假定产品故障为连续改进情况下,产品可靠性增长实际上是一个Weibull过程,并给出了产品失效率评估方法。在许多产品研制过程中,产品故障往往采用集中处理方式,此时,产品的可靠性增长呈现出阶梯增长。文献[1~3]针对阶梯增长情况提出了顺序约束Bayes评估方法,利用不同研制阶段的失效率的顺序约束条件对产品失效率进行评估。此外,文献[4]还提出了加速因子Bayes评估方法,文献[5]利用先验均值和先验分位数方法制定产品可靠性鉴定试验方案,试图充分利用产品可靠性研制试验信息来减少产品可靠性鉴定试验量。但是,上述文献在处理阶梯型可靠性增长试验数据时均没有考虑到产品各研制阶段的失效率减小幅度。事实上,在产品设计改进过程中,随着产品设计缺陷的不断被暴露,尽管产品失效率呈现出减小趋势,但其减小量却是逐步递减的。实际上,AMSAA模型在要求其增长参数小于1时描述了产品失效率减小量逐渐减小这一特征。因此,对于阶梯型可靠性增长试验信息的处理,不仅需要考虑产品失效率随着研制阶段的推进是顺序减小的,而且还需要考虑产品失效率的减小幅度是逐步减小的,以便客观评估产品正样阶段的可靠性。
本文在充分考虑产品在各个研制阶段的失效率减小幅度顺序减少的基础上,提出了产品失效率新的顺序约束条件,即产品失效率在相邻阶段的比值也应满足顺序减少约束。在此基础上,给出了一种新的产品失效率顺序约束Bayes评估方法,并基于上述评估方法研究了产品可靠性鉴定试验方案制定方法。通过算例数据分析,与传统的顺序约束Bayes评估方法进行对比,发现本文给出的评估方法更能准确评估产品失效率,所给出的可靠性鉴定试验量较传统的方法要大,反映了利用失效率减小量的顺序约束是必要的。
2 先验分布的确定
为了客观利用产品可靠性研制信息给出正样产品的失效率估计,本节首先研究产品失效率的先验信息,确定产品失效率的先验分布。
假设产品的整个研制过程分为m个阶段,其中前m-1个阶段为产品的样机试验阶段,第m个阶段为产品的(正样)定型阶段,并设第i个阶段产品寿命服从指数分布:

随着试验的不断进行,产品的缺陷逐步暴露,继而对产品进行改进,可靠性得到提高。此时产品的失效率满足顺序约束:

产品在试验过程中,产品设计缺陷得到不断暴露并被修正,其产品设计中的残留缺陷对产品可靠性的影响也越来越小,反映到产品失效率的变化上就是,产品失效率不仅需要满足传统的顺序约束条件(2),而且还应满足以下顺序约束:

新的顺序约束(3)实际上是要求在产品相邻研制阶段的失效率比值是顺序减少的,这表明随着产品设计改进,其可靠性增长幅度也越来越小。实际上,在常见的AMSAA模型中,当增长参数小于1时产品失效率随着研制过程的推进降低幅度也越来越小,因此,在阶梯型可靠性增长模型中,要求产品失效率满足新的顺序约束(3)是合理的。同时,新的顺序约束实际上包括了传统的顺序约束(2)。事实上,由于λ2/λ3>1,则

类似地,可以得到产品失效率在满足新的顺序约束(3)时,有λ1>λ2>…>λm>0。因此,顺序约束条件(3)是评估产品失效率时应使用的先验信息。
设产品失效率λi的无信息先验分布为其共轭分布,即
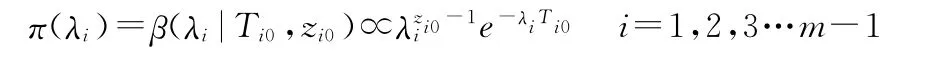
由Box-Tiao方法[5]可知,其中超参数取值为Ti0=0,zi0=0,所以产品失效率λi的无信息先验分布为

由于第m个阶段为产品正样阶段,在短时间试验情况下通常不会发生故障,因此,为能够正常处理正样阶段的可靠性研制试验信息,一般对正样失效率的先验分布中超参数取值较为保守,如由Box-Tiao方法[5]可知,λm的无信息先验分布为

由λ1,λ2,λ3,…,λm的独立性知,(λ1,λ2,λ3,…,λm)的无信息联合先验分布为

3 正样失效率λm的Bayes估计
假定产品在m个阶段的可靠性研制试验信息为(Ti,zi)(i=1,2,…,m),即在i个阶段,进行了总试验时间为Ti内,发生了zi次故障。这里试验包括定数截尾试验和定时截尾试验,则其似然函数为

设各阶段试验是相互独立的,则整个样机阶段的似然函数为

其中t={(Ti,zi),i=1,2,…,m-1}。
在有了产品在m阶段的可靠性研制试验信息的似然函数的基础上,利用(λ1,λ2,λ3,…,λm)的先验分布,就可以得到(λ1,λ2,λ3,…,λm,t)的联合密度函数为

联合密度函数g(λ1,λ2,λ3,…,λm,t)包含了所有正样失效率的信息,由Bayes定理得到定型产品失效率λm的后验分布为

其中

在平方损失下,正样失效率λm的Bayes估计为
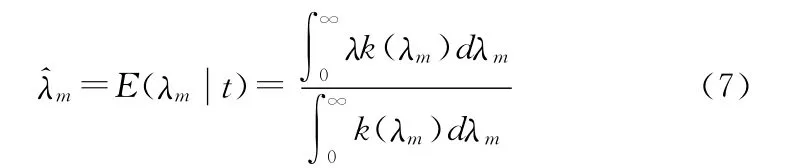
相应地,正样失效率λm的二阶矩估计为

特殊地,当m=3时,产品正样失效率λ3的后验分布可进行适当简化。利用不完全Gamma函数与Poisson分布累积项之间的恒等式[1]:

则

因此,产品正样失效率λ3的后验分布可简化为

4 产品失效率鉴定方案
随着产品可靠性要求越来越高,利用经典统计方法开展可靠性鉴定试验所需要的试验量较大,从而造成可靠性鉴定试验实施十分困难。因此,充分利用产品可靠性研制试验信息,制定产品可靠性鉴定试验方案,是减少鉴定试验量的有效途径。为此,本节将在产品正样失效率评估结果基础上,研究制定产品可靠性鉴定试验方案的方法。
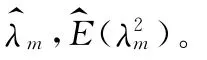

其中a与b为先验分布的超参数。


则

有了正样产品失效率λm的先验分布后,就可以制定产品可靠性鉴定方案[3]。假设产品可靠性鉴定方案为(c,Tc)(其中c表示最大允许失效数,Tc为总试验时间),在进行可靠性鉴定试验时,抽取n件产品,做有替换定时t0截尾试验,记总试验时间Tc=nt0,试验过程中失效产品数r服从Poisson分布:

由λm的先验分布式(9)和似然函数式(10)可以得到λm的后验分布:


假设规定使用方的风险为β,则有:

等价于P(λm≤λ′0|r=c,Tc,t)≥1-β,即

当给定c时,通过上式求解出相应的总试验时间,继而得到鉴定试验方案(c,Tc),当产品通过鉴定,则保证定型产品达到使用方要求的最小概率1-β,否则产品不能通过鉴定。
5 算例分析
为了说明本文提出的新顺序约束Bayes评估方法是有效的,本节处理某产品在研制过程中所获得的可靠性研制试验信息。该产品研制过程分为原理样机、初样机和正样机等三个阶段,在原理样机和初样机阶段分别获得的可靠性研制试验信息分别为(r1,t1)=(2,300),(r2,t2)=(1,1200),由于经过初样机的改进,工程技术人员认为该产品正样基本成熟,在该产品可靠性鉴定试验前没有组织专门的可靠性研制试验,即在正样阶段没有可靠性研制试验信息。
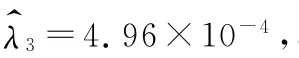
假定该产品设计要求最低寿命为10000小时,即其极限失效率为λ′0=1×10-4,规定使用方风险为β=0.2,利用新的顺序约束条件(9)得到先验分布的超参数为a=0.623,b=1255.2。基于上述先验信息,对于不同的合格判定数c,可得到相应的可靠性鉴定试验时间记为Tc,具体试验时间见表1第二行。为了对比该方案,在表1中列出了经典的可靠性鉴定试验方案(表1第一行)和基于传统的顺序约束Bayes评估结果得到的可靠性鉴定试验方案(表1第三行)。从三种鉴定试验方案可以看出,利用本文方法所得到的鉴定试验时间明显低于经典的可靠性鉴定试验时间,但比基于传统的顺序约束Bayes评估方法所得到的可靠性鉴定试验时间要长,这也说明考虑本文所给出的产品失效率顺序约束对产品可靠性鉴定试验方案有明显影响。从这个意义上来说,新的顺序约束条件(3)是客观评估正样产品失效率所必须要考虑的。

表1 利用不同方法得到的鉴定试验方案
6 结语
本文通过改进产品失效率的顺序约束,给出了产品失效率的新的顺序约束Bayes评估方法,并基于产品正样失效率评估结果,研究了可靠性鉴定试验的Bayes方案。通过实例分析表明,本文所给出的新的顺序约束条件对客观评估产品正样失效率,能够避免传统的顺序约束Bayes评估方法所得评估结果的冒进现象,对准确掌握产品可靠性增长规律具有重要意义。
[1]周源泉,翁朝曦.可靠性增长[M].北京:科学出版社,1992:260-263,120-127.
[2]茆诗松,汤银才,王玲玲.可靠性统计[M].北京:高等教育出版社,2008:106-107.
[3]张志华.可靠性理论及工程应用[M].北京:科学出版社,2012:260-263.
[4]张志华,姜礼平.指数型产品失效率鉴定试验的Bayes方案[J].应用概率统计,2000,16(1):66-70.
[5]陈宜辉,姜礼平,吴树和.指数分布下Bayes鉴定试验方案[J].运筹与管理,2002,11(2):56-59.
[6]Box,G.E.,Tiao,G.C.Bayesian Inference in Statistical A-nalysis[M].Addison-wesley Reading,1973.
[7]田艳梅,张志华.成败型产品验收试验方案研究[J].海军工程大学学报,2003,15(5):75-78.
[8]韩庆田,卢洪义,张毅.系统可靠性增长评估模型研究[J].航空动力学报,2009(11).
[9]周源泉.质量可靠性增长与评定方法[M].北京:北京航空航天大学出版社,1997.
[10]梅文华.可靠性增长试验[M].北京:国防工业出版社,2003.
[11]张金槐,张士锋.多层验前信息下可靠性增长的Bayes分析[J].质量与可靠性,2003(6).
[12]吴启光,李国英,赵勇辉.用于指数可靠性增长模型的一类新的先验分布[J].数学物理学报,2003(4).
