无人机测风速方案研究*
2013-11-28周旻王杰
周 旻 王 杰
(1.海军航空工程学院电子信息工程系 烟台 264001)(2.海军航空工程学院训练部 烟台 264001)
1 引言
目前,随着航空技术的发展,无人机在越来越多的领域得到了广泛的应用[1~5],这就对无人机的飞行性能提出了越来越高的要求,机载测风速技术已经成为了提高无人机飞行性能的关键技术之一[3~4],各国都在无人机测风速方面进行了大量研究,并取得了一系列成果。为此,本文对几种测风速方法进行研究,以找出适合长航时、大区域连续飞行的无人机的测风速方法,继而详细论述该种测风速方法的工作原理,以达到提高无人机风场测量精度的目的。
2 水平空速归零法分析

图1 无人机盘旋飞行时的水平投影
该方法利用无人机可以在水平面很小的半径范围内盘旋飞行的特点(如图1),盘旋飞行一圈,相对空气而言,飞机回到了同一点,水平空速矢量之和为零,平均水平风速等于飞机平均水平地速。
判断无人机盘旋飞行一圈的标志是航向传感器输出值相等。也就是说相对于空气而言,盘旋飞行一圈后,飞机回到同一点。则T时段飞机所在气层的平均水平风速Vw为
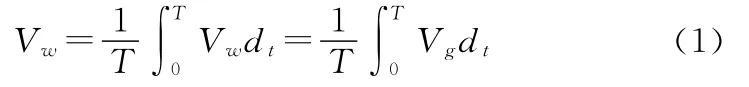
由式(1)可知,T时间段内无人机测得的水平风速只与地速Vg相关,T是无人机飞行一圈所需的时间。GPS每秒钟测量一次无人机的地速Vg,因此:
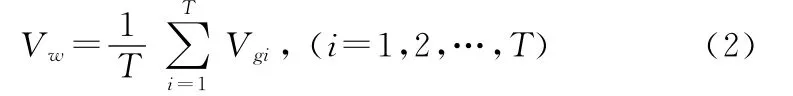
Vgi是GPS测量到的第i秒无人机的水平地速,Xi、Yi为通过GPS的经纬度算出的无人机的坐标值,则无人机地速Vg第i秒的x、y两个方向分量为

由式(3)可知,无人机的水平风速Vw的x、y两个方向分量为

水平空速归零法最大的优点是测量设备简单、测风速精度较高,误差小于1m/s,但是测风速方法繁琐,需要无人机在被测点上空盘旋飞行,既耗时又容易被战时击落,仅适合于常规场合下的定点测风速,不适合长航时、大区域执行侦察任务的无人机测风速。
3 航位推算法分析
其基本思想是根据相对运动、牵连运动及绝对运动三种运动的矢量合成关系,通过测量的无人机绝对运动位置及航位推算得到的无人机相对于大气云团的相对位置,对作为牵连运动的风场进行解算[6~7]。
利用推算出的无风时飞机位置和实际飞机位置差来计算出风速。设(X,Y)为飞机的实际位置坐标;(Xc,Yc)为不考虑风时航位推算出的飞机位置坐标,则有:

其中Vwx,Vwy分别为计算出的风速在x,y两坐标上的分量。由式(5)计算风速时,其标准差为下式[2]:

其中,t为时刻t2与时刻t1之间的间隔;σx1,σx2,σy1,σy2分别为t2时刻与t1时刻的x、y两个方向上无人机实际位置的测量标准差;ρx,ρy分别为X1与X2和Y1与Y2之间的相关系数。当ρx=ρy≜ρ,σx1=σx2≜σx,σy1=σy2≜σy时,有下式结论:
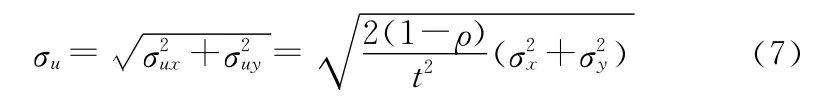
由式(7)可以看出,航位推算法求出风速的误差随着位置误差σx、σy的增大而增大,随着计算风速的周期t的减小而增大。若要获得即时的风场信息,即t很小时,计算出的风速的误差很大;或者当位置误差σx、σy较大时,求出来的风速的标准差也很大。所以该方法不适用于得到较准确的风场信息的要求。
航位推算法只适用于低成本配置的无人机测风速,因为该方法仅需要航向传感器、空速传感器以及惯导位置测量传感器等一些基本的测量元件,就可以解算风场,不足之处是解算频率相对较低,测风速精度较差,获得的风场信息不够全面。
4 平面矢量三角形法分析
无人机质心处的风速矢量Vw、无人机对地的固有速度矢量Vg(即地速)与无人机对空气的相对速度矢量Va(即空速)构成矢量三角形关系[8],即:

式(8)即为无人机测风速的基本原理。
无人机利用皮托-静压管[8]进行风场测量一直是无人机测风速领域的一个研究重点,该方法使用方便灵活、可大区域连续测量,估计频率相对较高,能够解算出小尺度变化的三维风场信息。其风速的解算需要用到空速、地速、姿态角和气动角等飞行参数。空速通过空速管测量得到的静压、动压和静温应用流体力学原理解算得出,地速由无人机的组合导航系统解算得出,气动角可由角度传感器直接测量。
由以上分析可知,要得到三维风速,除了需要空速值Va、地速矢量Vg外,还需测量无人机的姿态角和气动角的五个参数,即偏航角Ψ、滚动角φ、俯仰角θ、侧滑角β和攻角α。通常由于受气流的扰动,侧滑角和攻角的测量误差比较大,而且其校正又涉及到空速管和无人机纵向轴线的对准校正、空速管弯曲的校正、角速率影响的校正以及侧流和升流影响的校正,需要测量空速管在不同加速度载荷下的弯曲率以及三个姿态角速率等参数[8~9]。以上各参数的测量需要复杂的系统和解算过程,这就在一定程度上增加了研制经费和时间,同时因测量参数的增加又增加了输入误差源。当无人机保持水平飞行时,俯仰角、攻角以及侧滑角都很小,对测风速精度的影响可以忽略不计[10],由于本文主要考虑无人机飞行航迹控制问题,只需知道水平风场。

图2 水平面内风速矢量三角形示意图
图2中,Vg是地速;Va为空速;Vw是风速;Ψ 为航向角;Ψs是航迹角;Da为Vg和Va的夹角(航迹线至无人机纵轴的夹角),顺时针为正,称为偏流角;Dw为正北方向至水平风速方向的夹角,顺时针为正,称为风向角;
由图2中的三角形边角关系,可得风速风向的计算公式为

其中:

Dw中有π这一项,是由于气象上定义的风向和数学上定义的风矢量上的差别而引起的。
5 结语
在上述三种测风速方法中,水平空速归零法测量设备简单,但实时性差,不适合长航时、大区域执行侦察任务的无人机测风速,是气象上常用的一种测风速方法。航位推算法容易实现、算法简单、能实现大区域测量,但测风速精度较差。因此,上述两种测风速方法不适合无人机飞行过程中所需的实时风场测量,而平面矢量三角形法使用方便灵活、可大区域连续测量,估计频率相对较高,能够为无人机的飞行控制提供高精度的实时风参数。
[1]Etkin B.Turbulent wind and its effect on flight[J].Jounal of Aircraft(S0021-8669),1984,21(3):175-182.
[2]屈耀红,刑小军,闫建国,等.联合卡尔曼滤波在无人机组合导航中的应用[J].飞行力学,2004,22(4):69-72.
[3]刘林.在飞行中进行风场估计[J].飞行力学,1992,10(3):41-48.
[4]Malcolm J Abzug.Computional Flight Dynamics[M].USA AIAA Educational Series(S048-7180),1998.
[5]屈耀红.小型无人机航迹规划及组合导航关键技术研究[D].西安:西北工业大学博士论文,2006.
[6]屈耀红,凌琼,等.无人机DR/GPS/RP导航中风场估计仿真[J].系统仿真学报,2009:1822-1825.
[7]刘林.导航中的风场估计[D].西安:西北工业大学硕士论文,1989.
[8]William Gracey.Summary of Methods of Measuring Angle of Attack on Aircraft[R].NACA Technical Note 4351,1985.
[9]Haering E A.Air Data Calibration of High-Performance Aircraft for Measuring Atmospheric Winf Profiles[R].NASA Technical Memorandum 101714,1989.
[10]World Meteorological Organization.Aircraft Meteorological Data Relay(AMDAR)Reference Manual[R].WMO-No.958,2003.
