基于计算载荷谱的车下设备安装箱体疲劳寿命仿真分析

李国顺，储高峰，张义超

（中国铁道科学研究院 机车车辆研究所，北京100081）

产品结构的疲劳寿命是现代设计的一个重要指标，随着市场竞争的日趋激烈，产品的寿命对用户来说显得愈来愈重要。近20年来，随着CAD／CAE技术的突飞猛进，虚拟疲劳设计理念已经在许多行业得到了广泛应用。

满足安全性及可靠性要求的同时做到减轻质量和节省成本已越来越成为高速动车组结构产品设计师遵循的原则，其中，承载结构的疲劳耐久性设计就是必须面对的重要课题之一。长期以来，我国机车车辆承载结构设计主要采用传统的设计方法，以静强度理论为基础，根据实践经验将产品材料的屈服极限或强度极限与选取的安全系数之比作为承载结构设计的许用应力，根据现有相关标准对设计产品进行静强度和疲劳强度分析，并采用试验室静强度试验和疲劳强度试验方法来校核结构的强度是否满足设计和线路运行要求。这种设计思路对于结构全寿命周期内所承受的载荷比较明确时，一般可以获得比较可靠的强度评价结果。但对于受力状态不明确或者结构细节特征知识不充分，以及无法通过试验室试验来对结构部件进行疲劳性能进行评价等情况下，采用现行标准就可能无法对这些承载结构进行合理的强度评价。然而，通过样机生产出来后再行通过线路试验来对这些承载构件进行可靠性分析和结构优化，不仅周期长，而且成本也会大幅增加，这时，虚拟样机动力学与结构疲劳强度仿真技术不仅是对这些结构进行疲劳强度分析最好的手段，同时也能大幅度缩短产品设计周期和降低成本。

本文以动车组车下悬吊的设备箱体为研究对象，采用车辆动力学与结构疲劳可靠性协同仿真的方法对被研究对象的结构可靠性进行了仿真研究。

1 箱体载荷谱仿真分析

1.1 整车仿真模型建立

按多体动力学理论，动车组模型可视为复杂的多刚体、多自由度的系统来处理。整车仿真模型主要由轮对、构架和车体等质量体构成，轮对、构架和车体间通过弹簧、阻尼等力元连接。动力学仿真模型见图1所示。轴箱悬挂模型包括由轴箱弹簧提供的3个方向刚度、由轴箱定位装置提供的刚度，一系悬挂垂向阻尼则由悬挂在轴箱弹簧外侧的一系垂向减振器提供。二系悬挂模型包括空气簧提供的3个方向的刚度，抗侧滚扭杆刚度、横向止档刚度以及垂向、横向、抗蛇行减振器提供的阻尼。车下悬吊箱体设备通过4个弹簧力元将质量块连接到车体底架上进行模拟。

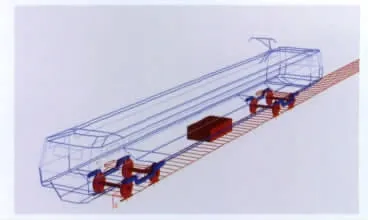
图1 整车仿真模型

1.2 轮轨接触几何关系

轮轨接触基本情况如图2所示，其中轨距为1 435 mm；轨底坡为1／40；车轮采用S1002G踏面；轨道采用60kg／m钢轨（TB／T 2341.3）。

图2 轮轨接触几何关系

1.3 轨道不平顺

铁路轨道在列车车轮的作用下，轨面会产生不均匀磨耗。由于轨道的垫层、轨枕、道床和路基的弹性不均、各部件之间的间隙等原因将导致轨道的几何形态发生变化，出现不平顺，研究表明轨道不平顺是一个随机过程。

本次计算模型中以京沪高铁的一段实际测量的不平顺作为线路激扰输入。为了对实际输入线路不平顺有个大致了解，我们将其功率谱和德国的高低干扰谱进行了比较，图3和图4分别是高低和轨向不平顺功率谱图。从图中可以看出，在2m以下的短波不平顺中，京沪线实测高低不平顺略大于德国高干扰谱，轨向不平顺介于高干扰谱和低干扰谱之间。而在2m以上的长波不平顺中，京沪线实测高低和轨向不平顺都小于德国低干扰谱。

图3 高低不平顺功率谱

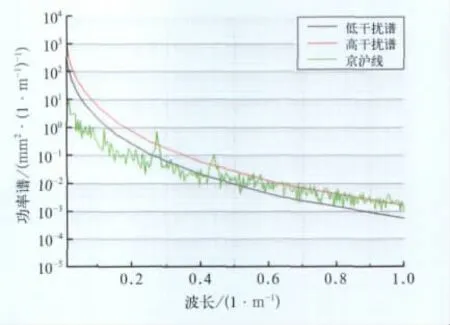
图4 轨向不平顺功率谱

1.4 计算线路工况

振动载荷仿真计算线路选择一段半径为R7 000m的曲线和一段直线进行模拟。其中，直线线路长度为30 000m，曲线线路平断面情况如表1所列。

表1 计算线路工况

1.5 计算结果

对于车体下悬吊的箱体来说，在动车组运营中，其承受的载荷除箱体中各种电气设备的质量外，其所承受的动态载荷主要为运行中产生的惯性载荷。图5和图6为动车组车下悬吊箱体质心位置处垂向和横向振动加速度的计算结果。

图5 箱体垂向振动加速度图

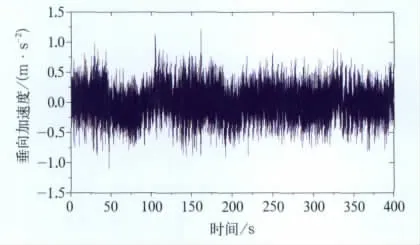
图6 箱体横向振动加速度

2 箱体应力分布仿真分析

2.1 有限元仿真模型

通过建立车下悬吊的箱体结构有限元仿真模型，应用有限元仿真软件计算箱体在其内安装的各种设备自重作用下的应力，进而得到该箱体的应力分布。

基于有限元分析软件建立了箱体有限元计算模型，如图7所示。将箱体离散成三维壳单元SHELL93，将箱体安装销轴离散成三维实体单元SOLID186。计算模型节点总数为94 710，单元总数为29 485。

图7 箱体有限元计算模型

2.2 计算载荷

在箱体有限元计算中，垂向载荷考虑安装于箱体内部的各种设备以及箱体自身在垂向振动加速度为14.27 m／s2（1.5g，按照标准EN 12663-2010和《200km／h及以上速度级铁道车辆强度设计及试验鉴定暂行规定》选取）时引起的垂向惯性载荷。

横向载荷考虑安装于箱体内部的各种设备以及箱体自身在横向振动加速度为9.81m／s2（即1.0g，按照标准EN 12663-2010和《200km／h及以上速度级铁道车辆强度设计及试验鉴定暂行规定》选取）时引起的横向惯性载荷。

2.3 计算边界条件

2.3.1 箱体约束条件

箱体采用4个销轴吊挂于车体两个横梁上，销轴与悬挂梁之间采用了弹性橡胶关节，对箱体起到一定的减振作用。因此，有限元计算中，在箱体吊挂的4个销轴处采用弹性约束对箱体的垂向、横向及纵向进行约束。

2.3.2 载荷施加方式

作用于箱体上的载荷主要有箱体本身的质量及箱体内部安装的各种电气设备质量，针对箱体内部设备安装的方式不同，分别采用不同的载荷施加方式。

（1）箱体垂向载荷与横向载荷：采用分布载荷方式均匀施加于箱体上；

（2）偏心质量体引起的载荷：由于设备的质心不在安装位置，其引起的载荷简化为作用于安装区域的垂向载荷和横向载荷及一个力矩。垂向载荷和横向载荷在安装区域以分布载荷的形式均匀施加；

（3）其他设备引起的载荷：其他设备引起的垂向载荷和横向载荷均采用分布载荷的形式在安装区域均匀施加。

2.4 应力分布计算结果

图8给出了箱体在设备振动载荷作用时的应力分布云图，图9和图10分别给出应力较大的电气设备安装梁区域和箱体吊挂销轴附近的应力分布云图。

图8 箱体应力分布图

图9 电气设备安装梁区应力分布

图10 箱体吊挂销轴附近应力分布

应力最大值出现在电气设备安装梁区域（如图9），箱体吊挂销轴附近区域的应力也比较大（图10），其他应力较大的区域均为各设备安装梁与箱体主框架连接的区域。最大应力值为96.7MPa。

3 箱体疲劳寿命仿真分析

3.1 箱体疲劳寿命仿真分析模型

箱体的疲劳寿命仿真采用专用的结构疲劳寿命仿真软件进行分析，其仿真模型采用概要流程图方式建立，对于车下悬吊的电气设备安装箱体结构的疲劳寿命仿真分析，建立了由箱体应力分布场输入模块、载荷时间历程输入模块、应力—寿命仿真分析模块、仿真结果图示模块、仿真结果存储模块以及危险点探测与输出模块组成的疲劳寿命仿真分析模型，选择应力—寿命方法作为箱体结构寿命的仿真分析方法，该方法基于Palmgren-Miner线性累积损伤理论，利用材料的S-N曲线和Goodman曲线计算结构的疲劳寿命分布以及损伤分布，确定结构的疲劳薄弱位置。

3.2 计算载荷

在箱体疲劳寿命仿真计算中，垂向载荷和横向载荷考虑安装于箱体内部的各种设备质量以及箱体自身的质量在动车组运行期间由于振动而引起的惯性载荷。图11列出了一个垂向惯性载荷和一个横向惯性载荷的时间历程示例，其中，图11（a）为由于箱体质量引起的垂向惯性载荷，图11（b）为安装于箱体中的电气设备质量引起的横向惯性载荷。

3.3 计算边界条件

3.3.1 材料特性

箱体结构采用的材料为S355J2H，其母材屈服极限为355MPa，抗拉强度中值为500MPa，根据标准TB／T 2368-2005《动力转向架构架强度试验方法》，该材料的Goodman曲线如图12所示。材料S355J2H的S-N曲线如图13所示。

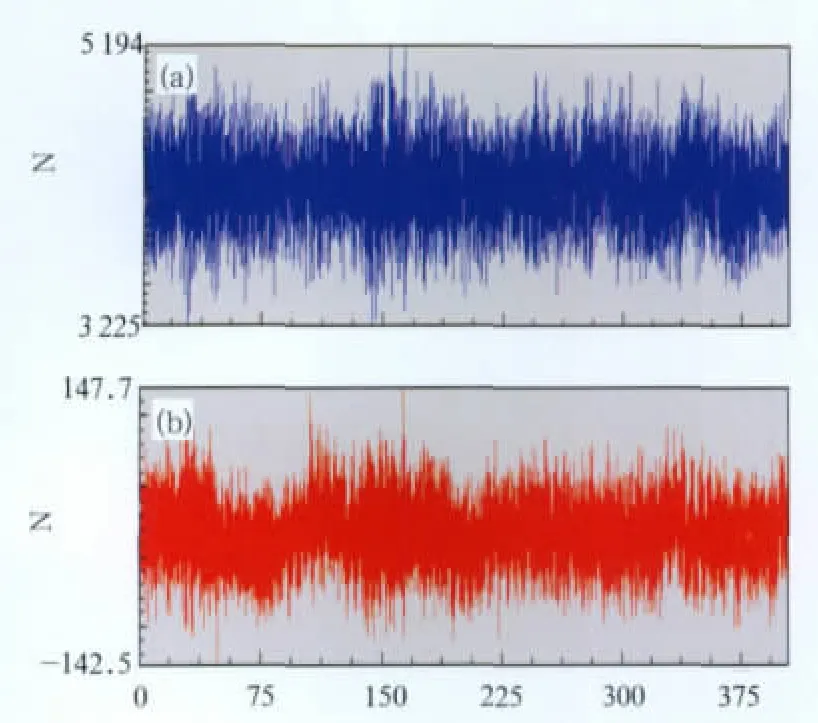
图11 箱体垂向惯性载荷和设备横向惯性载荷

图12 箱体结构材料Goodman曲线

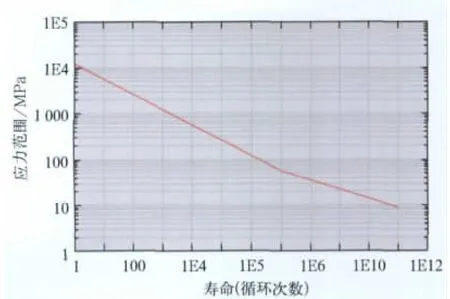
图13 箱体结构材料S－N曲线

3.3.2 载荷时间历程及施加方式

通过转换工具将动力学仿真计算得到的箱体质量以及箱体中各个设备质量引起的垂向惯性载荷和横向惯性载荷时间历程转换成疲劳寿命仿真分析软件所需要的载荷时间历程，该载荷时间历程以分步方式记录，即每个载荷均作为一个单独的时间载荷步，共分为19个载荷步，并采用以下方式施加载荷：

（1）箱体垂向惯性载荷与横向惯性载荷：采用分布载荷方式均匀施加于箱体上；

（2）偏心质量体引起的惯性载荷：由于质心不在安装位置，其引起的惯性载荷简化为作用于安装区域的垂向惯性载荷和横向惯性载荷及一个惯性载荷力矩。垂向惯性载荷和横向惯性载荷在安装区域以分布载荷的形式均匀施加；

（3）其他设备引起的惯性载荷：其他设备引起的垂向惯性载荷和横向惯性载荷均采用分布载荷的形式在安装区域均匀施加。

3.3.3 箱体应力分布场

箱体应力分布场是进行箱体结构寿命仿真分析的主要输入参数之一，通过有限元软件对箱体进行有限元仿真计算，从而获得该箱体的应力分布场，不同载荷在有限元计算时按照载荷步方式依次施加，即每个载荷均作为一个单独的时间载荷步，共分为19个载荷时间步，通过计算分别得到各载荷步下的应力分布场。

3.4 箱体疲劳寿命计算结果

表2给出了箱体结构疲劳寿命仿真计算结果前十个最小寿命节点的损伤量、京沪高速往返运营次数以及等效运行公里数，图14给出了用运营公里数表示的箱体结构的等效寿命分布云图，图15～图17分别给出了前3个最小寿命的节点具体位置及附近的等效寿命分布云图。

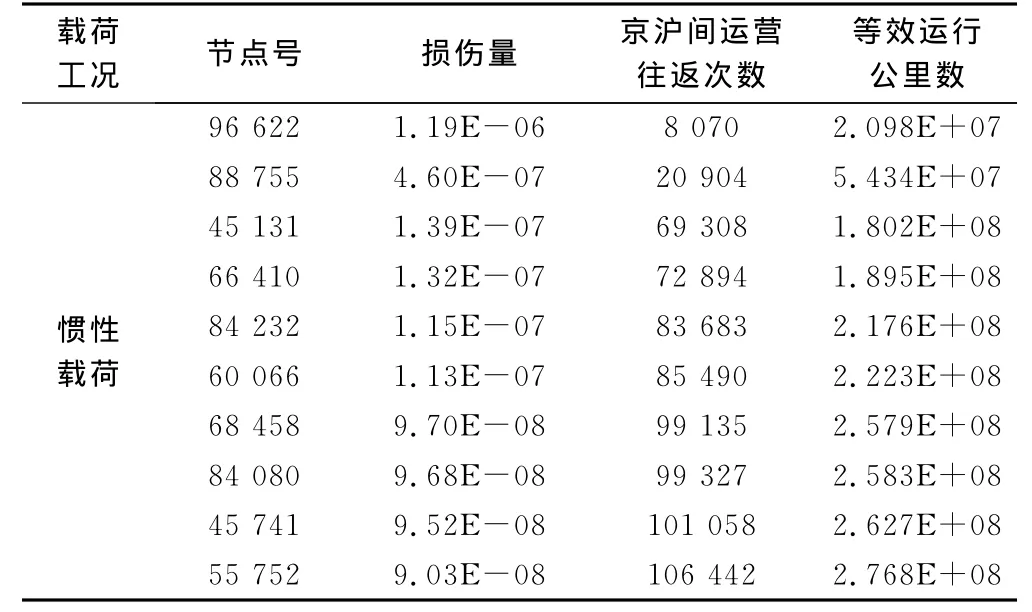
表2 箱体疲劳寿命计算结果

图14 箱体等效寿命分布图

图15 箱体最小等效寿命节点位置

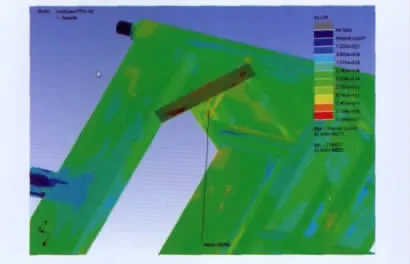
图16 箱体第2小等效寿命节点位置

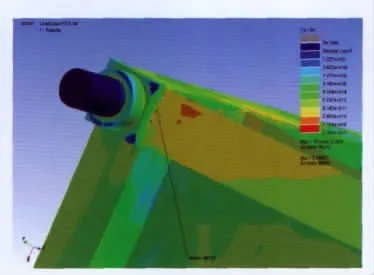
图17 箱体第3小等效寿命节点位置

从仿真计算结果可以看出，最小寿命出现于箱体框架底架纵梁与端横梁焊接处，最小寿命为2 098万km，按照京沪高铁往返一次计算，约能运行8 070个往返。第2小寿命出现在电气设备在箱体中的安装支架上，第3小寿命出现在箱体吊挂销轴与箱体本体焊接处。

4 结束语

本研究分别建立了动车组车辆的动力学仿真计算模型、车下悬吊设备箱体结构有限元仿真计算模型和箱体结构疲劳寿命仿真计算模型。通过动力学仿真计算，获得了箱体的垂向和横向振动加速度时间历程以及箱体内各质量体的垂向和横向振动惯性载荷；通过对箱体进行有限元仿真计算，获得了箱体各载荷步的应力分布场；利用动力学和结构有限元的仿真计算结果作为箱体结构疲劳寿命仿真分析的输入，通过对箱体结构疲劳寿命仿真计算，获得了箱体结构的疲劳寿命。研究表明，多体动力学与结构有限元、结构疲劳寿命协同仿真分析方法为在设计阶段预测车下悬吊设备结构的可靠性提供了有效的手段，可以用于结构设计阶段的疲劳强度校核和结构动态优化。

［1］卜继玲.动车组系统动力学与结构可靠性［M］.北京：中国铁道出版社，2009.

［2］米彩盈.铁道车辆结构强度［M］.成都：西南交通大学出版社，2007.

［3］朱 涛.基于实测载荷谱的白车身疲劳寿命计算［J］.汽车技术，2009，（5）：8-10.

［4］TB／T 2368-2005.动力转向架构架强度试验方法［S］.北京：中国铁道出版社，2005.

［5］EN 12663-2010.Railway applications-Structural requirements of railway vehicle bodies［S］.CEN，2010.