大型风力发电机复合材料叶片动态特性分析*

□ 郑玉巧 □ 赵荣珍 □ 刘 宏

兰州理工大学 数字制造技术与应用省部共建教育部重点实验室 兰州 730050

风力发电机叶片是风力机捕获风能的关键部件，其结构和强度对风力机的可靠性起重要作用。由于玻璃钢/复合材料的高强度和低弹性模量的特性，国内外已普遍采用玻璃钢/复合材料的叶片［1］。大型风力机叶片在高空中作大范围空间运动，由于旋转惯性力、气动力、重力等因素引起耦合效应,部件表现出明显的几何非线性特征,即惯性载荷导致叶片的局部或整体刚度发生改变。加之叶片结构是个展向长、弦向短的细长体，柔性好，容易发生振动，其振动不仅会引起叶片的附加应力，而且影响叶片自身气动性能及其结构强度。叶片在工作过程中经受较大振动和变形，不仅影响整机稳定性，而且影响叶片自身的气动性能。因此，在风力机机组的设计过程中，必须考虑叶片的结构动力特性及其动态响应［2］。有限元法是求解叶片结构振动特性的一种有效方法,由于叶片结构设计时要调整结构布局和材料铺层方案,加之叶片结构的复杂性,数值分析的效率较低,而有限元法由于具有较多自由度，计算精度较高，因此可以准确地模拟风力机叶片柔性结构的力学行为［3］。

1 叶片有限元动力学方程

假设叶片的有限元单元为线弹性体,并处于小变形范围内,且有限元内场变量的变化可以用一种简单的函数来近似,这些近似函数（也称为插值模式）可由场变量在节点处的值确定。由平衡、物理、几何三方程可导出结构的有限元基本方程［4-5］:

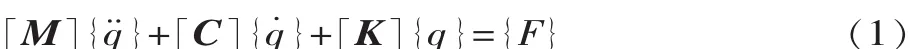
式中：［M］为系统质量矩阵；［C］为系统阻尼矩阵；［K］为系统刚度矩阵。

在非零的初始条件下,式（1）有非零解,反映了结构本身固有的特性,这就是结构的固有频率与振型,在数学上称之为特征值与特征向量。在实际工程中,由于阻尼对结构自振频率及振型影响不大，因而在讨论结构的固有特性时,常不计阻尼作用。令q=｛φ｝sin（ωt+θ）代入,根据瞬时最小势能原理可以导出叶片在时变载荷作用下的多自由度运动方程［4］:

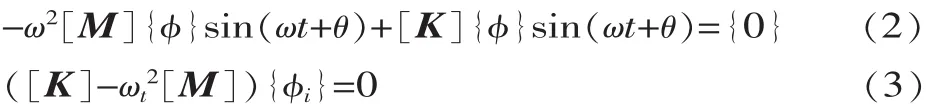
式中： ｛φi｝为第 i阶模态的振型向量（特征向量）；ωt为第i阶模态的固有频率ω2的特征值。

风力机叶片与轮毂间的连接可认为是固定连接,即叶片根部节点的自由度被约束,也就意味着根部节点的位移、转角均为零。对式（3）在上述约束条件下采用拟波前子空间迭代法求解,可以求得前五阶的固有频率和振型。

2 参数化建模

▲图1 NACA63-421翼型图

风机叶片的外形与内部结构较为复杂，一般由前缘、后缘、梁帽、腹板等不同区域组成。不同的区域具有不同的复合材料铺层，因此在结构分析的三维壳模型建模过程中,必须把叶片壳体按照铺层方式的不同分为不同的材料面，以便对其赋予各自的复合材料参数。叶片翼型截面曲线是由若干点光滑连接而成，故可由软件Profili导出NACA63-421翼型图，如图1所示。有限元模型基于有限单元法，把一个连续体或结构，离散为若干单元组成的等效离散，单元之间通过节点连接，单元内部待求量可以通过单元节点量，按指定的函数关系插值求得。由于叶片形状复杂,采用Pro/E图形软件,根据29.5 m叶片的几何数据,生成命令流文本,导入Pro/E中,进行建模和前处理。再将所建立的叶片模型文件生成IGES格式,供ANSYS读取有限元模型（见图2），叶片根部采用预埋金属螺杆,便于与轮毂连接［6］。这样的叶片根部连接被认为是刚性的,根部所在节点的6个自由度被固定,整个叶片简化为悬臂梁模型。

▲图2 有限元模型

2.1 模型参数的设置

在ANSYS中,选用Shell99单元，Shell为夹芯结构。在定义材料性能参数时，主要采用定义实常数的方式模拟材料的性能、铺层角和铺层厚度。然后选择合适的单元尺寸进行网格划分，最终可模拟叶片的实际铺层结构,根据蒙皮的不同厚度划分区域。叶片主要技术参数见表1。

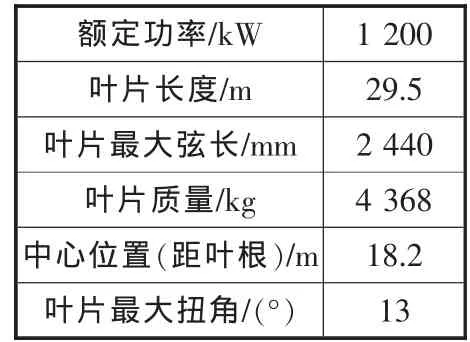
表1 叶片主要技术参数

2.2 叶片网格的划分

由于叶片形状的复杂性，叶片不同位置处单元属性、材料性能都不相同，所以应分段划分网格。叶片的铺层情况复杂：沿叶片纵向分布不均，沿叶片横向也不均匀，这就给单元属性的赋值带来了很大的困难，采用分段分块定义层合板模型，然后再分段分块将模型赋给单元。在划分叶片网格时,将Shell99单元通过主菜单 Preprocessor—Meshing—MeshTool进行网格划分,划分时采用映射与自由划分的方式来控制网格精度。划分后的有限元模型中，单元个数是13 487个，节点数是9 725个。叶片铺层主要参数见表2。

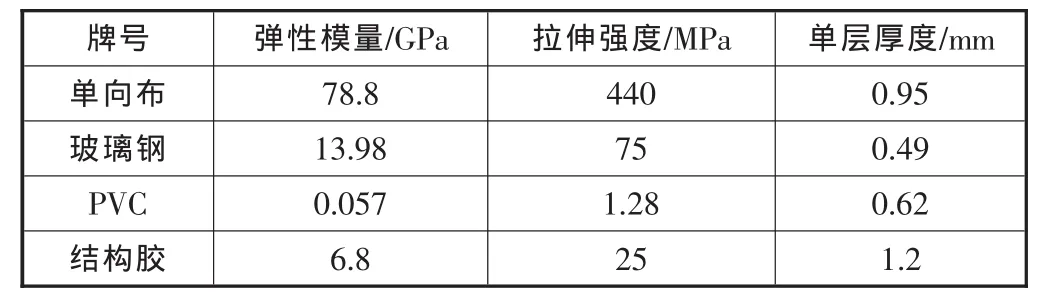
表2 铺层主要参数

2.3 固有频率和主振型的计算

由于叶片根部与轮毂的连接可近似认为是固定约束，因此在叶片根部施加固定约束，其它部位不受力，将ANSYS模态分析的计算频段指定为0～1 000 Hz,并指定模态提取数为10，模态扩展数为10。本文采用分块Lanczos算法对叶片进行模态分析，求解叶片前五阶自由振动频率和模态。前五阶自由振动频率值见表3，主振型如图3～图7所示。

表3 复合材料叶片前五阶频率

3 模态计算结果及分析

1）前二阶振动形式为挥舞振动，这说明弯曲振动（包括挥舞和摆振）频率较低；是风力机叶片的主要振动形式；叶片三阶振动即摆振振动；以后各阶为这两种形式的单独振动或颤振弯曲自振频率随转速略有增加。另外，挥舞和摆振的固有频率较低,而扭转振动的影响较小。

▲图3 一阶振型图

▲图4 二阶振型图

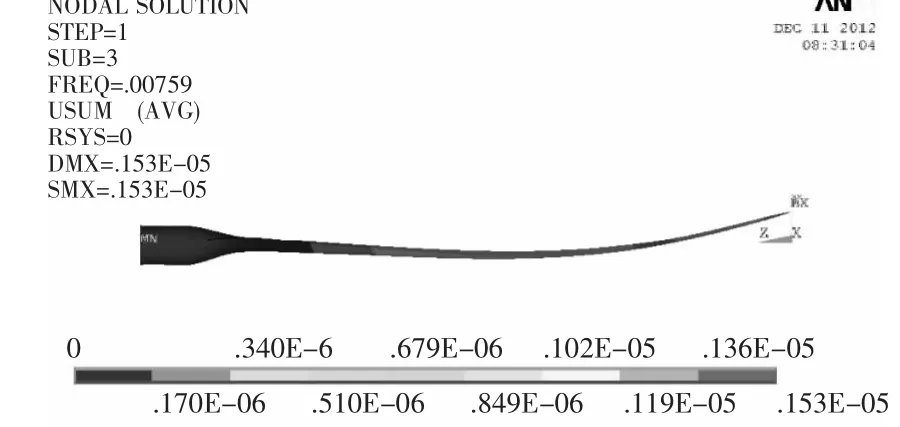
▲图5 三阶振型图

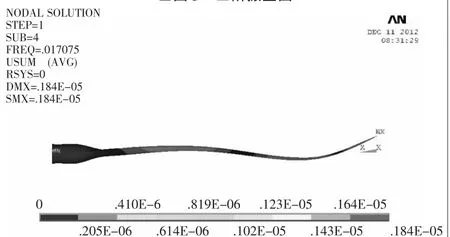
▲图6 四阶振型图

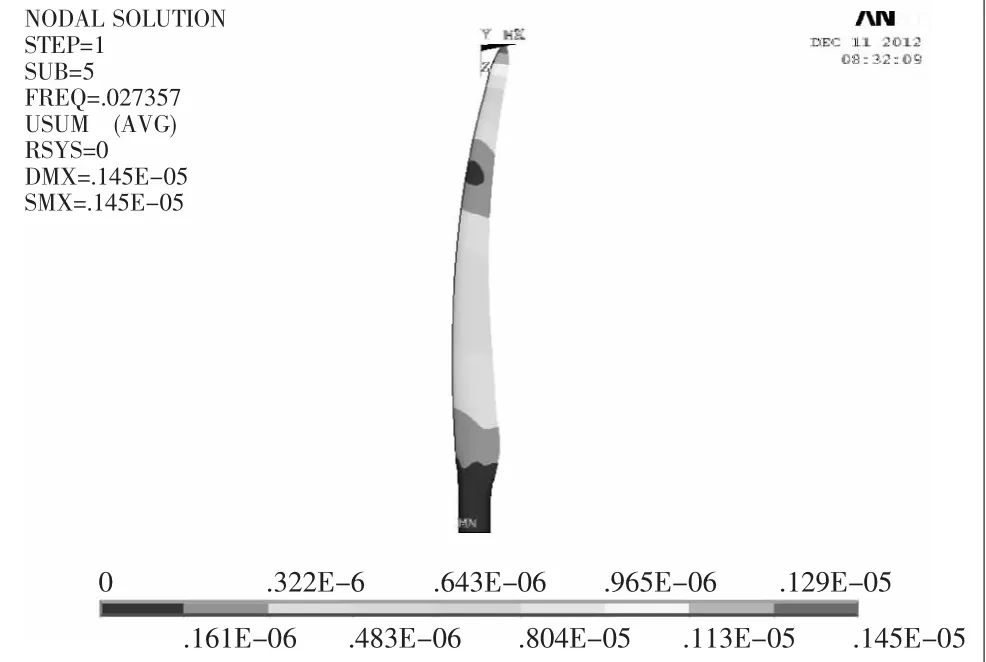
▲图7 五阶振型图

2）铺层方向还将影响翼面的固有振动特性，主要表现在固有频率的变化及节线位置的改变。因此，在设计叶片时，应重点考虑挥舞和摆振的频率和模态。为了不使叶片发生共振，必须避免低倍频激振频率和风力机自振频率整数倍重合。

4 结论

本文开展了大型复合材料风机叶片二维壳模型的参数化建模技术以及基于薄壳模型的叶片模态分析技术,通过实常数赋值来实现对叶片铺层的模拟，较为真实地模拟了叶片的实际结构。在计算中，把风力机叶片的振动分为垂直于旋转平面的挥舞振动、旋转平面内的摆振振动及绕叶片轴线的扭转振动，分别计算了其前五阶的固有频率和振型。该计算方法可应用于风力机的叶片结构特性分析。

［1］ 戴春晖,刘钧,曾竟成,等．复合材料风电叶片的发展现状及若干问题的对策［J］.玻璃钢/复合材料,2008，17（1）：53-56.

［2］ Mahmood M Shokrieh,Roham Rafiee，Simulation of Fatigue Failure in a Full Composite Wind Turbine Blade ［J］.Composite Structures，2006，74 ：332-342.

［3］ Diego Cárdenas，Alejandro A Escárpita.Numerical Validation of a Finite Element Thin-walled Beam Model of a Composite Wind Turbine Blade ［J］.Wind Energy，2012，15（2）:203-223.

［4］ 刘雄,李钢强,陈严，等.水平轴风力机叶片动态响应分析［J］.机械工程学报,2010,46（12）:128-130.

［5］ 诸德超,邢誉峰.工程振动基础［M］.北京：北京航空航天大学出版社，2004.

［6］ 郑玉巧，黄建龙.基于有限元分析的单立柱堆垛机结构优化与改进［J］.组合机床与自动化加工技术，2010（9）：83-85.