电磁发射轨道受指数函数磁压力的瞬态响应

刘 峰，刘 文

(燕山大学 理学院，河北 秦皇岛 066004)

电磁发射技术是利用电磁发射弹丸射程远、速度快、杀伤力大；射击无声响、无烟雾、无炮口火焰, 具有良好的射击隐蔽性；射程调整方便, 不受推进剂原料的影响；电能可用任何初级能源来产生等优点，因此，电磁发射技术将在炮弹发射、导弹发射、鱼雷发射、火箭弹发射、飞机弹射及航天发射等技术领域得到广泛应用，其军事应用潜力非常大。近几年，美国陆军正在进行弹丸速度为2.5 ～4km/s的电磁炮研究，以期作为未来主战坦克的主炮，形成新的反装甲能力。随着电磁发射技术的日趋成熟，电磁炮将在21世纪逐步走向武器化，在军事领域将获得广泛应用[1-2]。

国内前期做的研究大都是对低于四阶或四阶偏微分方程的求解，目前尚未有人研究过高于四阶偏微分方程的初边值问题的求解，影响轨道的弹性摩擦阻尼力的因素也不例外，因而研究其影响因素是非常有意义的。本文通过求控制方程解析解研究了影响梁动力响应因素，将电磁发射装置轨道看作移动载荷作用下弹性基础上的简支梁，借助积分变换及其逆变换等方法求其解析解，借助软件编程及运行结果显示：梁的动态响应受摩擦阻尼系数，材料阻尼系数，弹性系数的影响程度不同。

1 发射原理

电流流经导轨、电枢及在其周围形成强磁场，该磁场和流经电枢的电流互相作用，产生强大的电磁力，推动了电枢及其前面发射载荷沿导轨做加速运动，直到将载荷发射出去为止。

初值条件及边界条件[3-5]为：

(1)

式中:ψ为梁的挠度。

2 求解控制方程的积分变换法

研究问题的控制方程为：

(2)

式中：cs为梁材料应变阻尼系数;λ为弹性基础的弹性常数;c为弹性基础粘滞外阻尼系数;梁单位长度质量m=ρlh,ρ为轨道材料密度;l和h分别为轨道梁横截面宽和高度;EI为梁的抗弯刚度;函数qeixu(x)指以速度v沿着轨道向前传播的电磁力，v由Heaviside单位阶跃函数H(x-vt)表示，其中u(x)=[1-H(x-vt)]。

由初始条件和边界条件，对式(2)关于t、x进行拉普拉斯变换，得到:

(3)

(4)

(5)

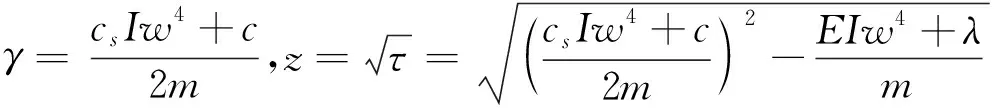
(6)

1)当z≠0，φ>0时，z为实数，则对(4)进行拉普拉斯逆变换，再计算，将式(6)代入得:

(7)

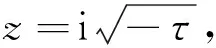
(8)

3)当z=0时，α1=α2=-γ，进行拉普拉斯逆变换再借助求解留数的方法计算得到:

(9)

对式(7)、(8)、(9)进行傅里叶逆变换，得:

(10)

(11)

(12)

探讨z为实数或虚数时的情形：

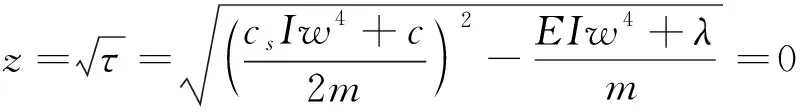
解得:

(13)

式(13)的根为:

k=0,1,2,3

(14)

其中，β1、β2分别为σ1、σ2的辐角主值。

1)σ1>0,σ2>0由式(14)知，σ1>σ2,式(13)在w∈(0,+∞)上有两个实根w1,2=|σ1,2|1/4=σ1,21/4， 在w∈(0,w2)，w∈(w1,+∞) 上，φ>0,z为实数；在w∈(w2,w1)上，φ<0，z为纯虚数。

2)σ1>0,σ2<0由式(14)知w=σ21/4无实根，w=σ11/4有两个相异的实根：x1=-|σ1|1/4=-σ11/4<0，x2=|σ1|1/4=σ11/4>0。

当w∈(0,x2)时，φ<0,z为纯虚数，当w∈(x2,+∞)时，φ>0,z为实数。

3)σ1<0,σ2<0或σ1,σ2为虚数，由式(14)知，式(13)无实根。当w∈(0,+∞)时，恒有φ>0，z为实数。

4)σ1=σ2=0，由(14)知式(13)当w=0时有唯一根，φ(0)=0，w∈(0,+∞)时，φ>0,z为实数。

3 动态响应的解析解

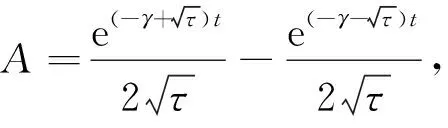
上面对z值的不同情况的讨论结果，得到轨道梁动力响应解析解ψ(x,t)有以下形式：

1) 当z≠0，σ1>0,σ2>0时

①L>w1

(15)

②w1>L≥w2

(16)

③w1>w2>L

Aeiwxdw

(17)

2) 当z≠0,σ1>0,σ2<0时

①L>x2

(18)

②L≤x2

Leiwxdw

(19)

3) 当z≠0,σ1<0,σ2<0或者σ1=σ2=0或者σ1、σ2为虚数时，轨道梁响应解析解ψ(x,t)与式(15)相同。

4) 当z=0时

Peiwxdw

(20)

式(15)～(20)为简谐压力移动载荷作用下轨道的动态响应解析解的表达式。

4 数值算例

通过所求轨道瞬态响应的解析式，编程显示，分析各系数数对轨道瞬态响应的影响。轨道及荷载参数见表1。

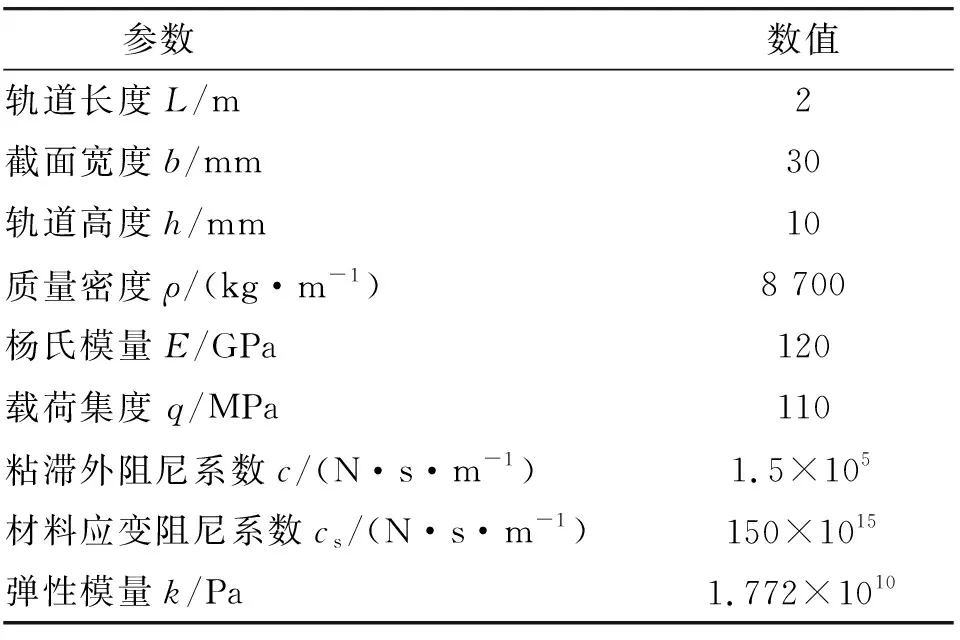
表1 轨道和荷载相关参数

图1是轨道梁挠度受到粘滞外阻尼系数的影响曲线。能够在图上看出粘滞外阻尼系数对轨道梁挠度的影响很显著，轨道梁挠度随着粘滞外阻尼系数的增大而减小。

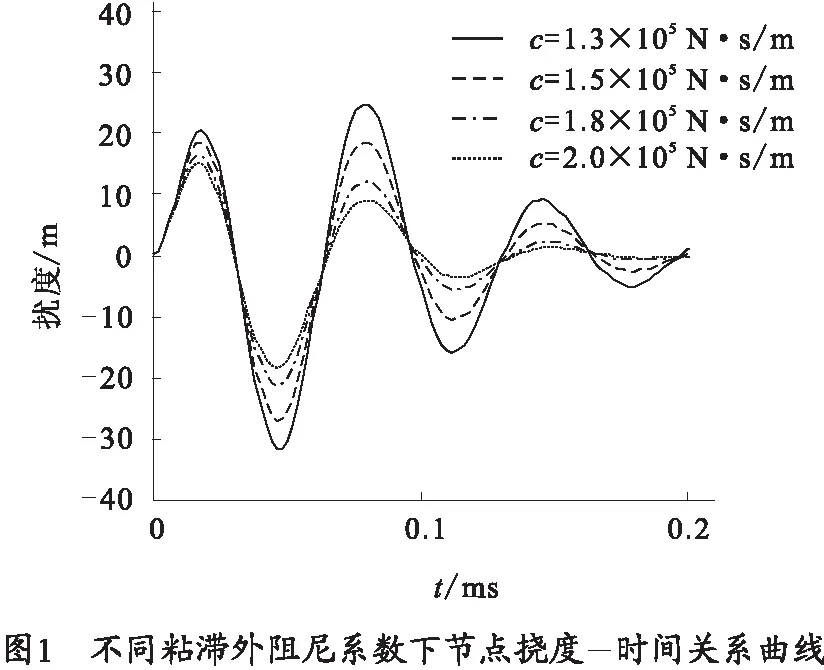
图2是材料应变阻尼系数对轨道梁挠度的影响曲线。材料应变阻尼系数对挠度有显著影响，轨道梁的最大变形挠度随着材料应变阻尼系数的增大而增大。

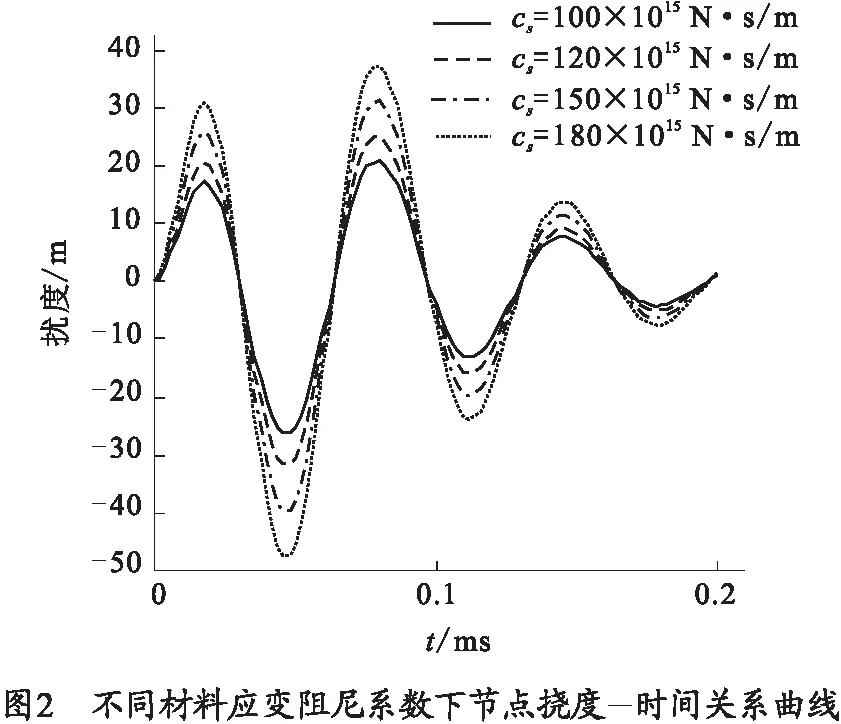
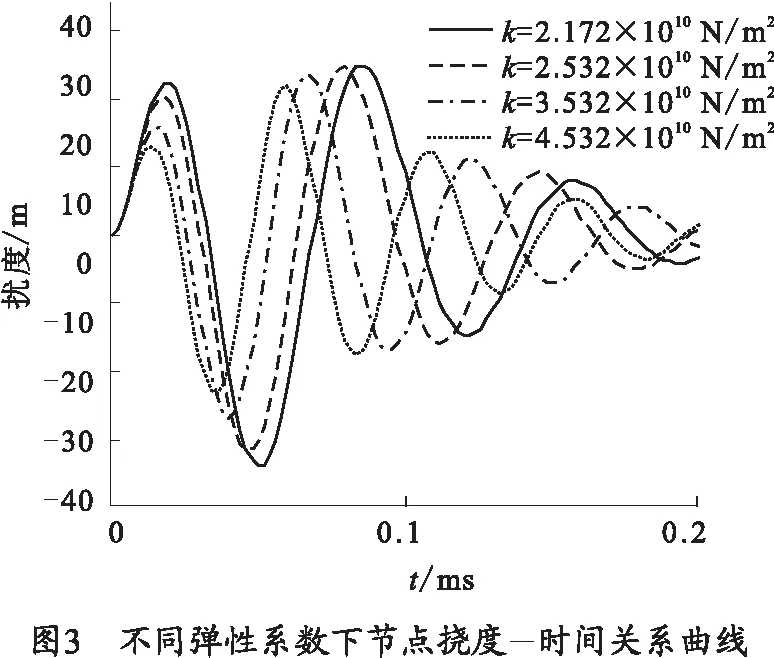
图3是弹性系数对轨道梁挠度的影响曲线。弹性系数对挠度的影响不明显，挠度曲线随着弹性系数的增加而呈下降的趋势。

5 结 论

在求解控制方程解析解的基础上，研究了影响梁瞬态动力响应的主要因素，将电磁发射轨道模拟为移动载荷作用下弹性基础梁，考虑阻尼力的因素，推导出控制方程的解析解，同时分析了形态压力对电磁发射轨道的瞬态影响。这可以更好的理解电磁轨道发射装置的工作性能，为电磁发射装置的设计提供了理论依据及技术支持，可提高其安全性、可靠性。

计算分析表明：材料应变阻尼系数、粘滞外阻尼系数、弹性系数对轨道梁挠度产生的影响呈现周期性的变化，在一个周期内，轨道梁的挠度随着粘滞外阻尼系数的增大而减小。随着材料应变阻尼系数的增大而增大。而弹性系数对挠度的影响不太明显，挠度曲线随着弹性系数的增加而呈下降的趋势。

[1] 古刚，向阳，张建.国际电磁发射技术研究[J].舰船科学技术，2007,29(1):156-158.

GU Gang,XIANG Yang,ZHANG Jian. International electromagnetic launch technology[J].Ship Science and Technology, 2007,29(1): 156-158.(in Chinese)

[2] 王静端.电磁发射技术的发展及其军事应用[J].火力与指挥控制，2001,26(1):5-7.

WANG Jing-duan.Development of military applications of electromagnetic launch technology[J].Firepower and Command and Control, 2001, 26(1):5-7. (in Chinese)

[3] LIU Wen, SHAN Rui. Mathematic model and analytic solution for a cylinder subject to exponential function[J]. Chinese Journal of Mechanical Engineering, 2009, 22(4): 587-593.

[4] LIU Zhu-bai, SHAN Rui, LIU Wen, et al.Solution of a hollow thick-wall cylinder subject to quadric function pressures and its limit when →∞[J] .Science in China：Series E, 2004, 47(2):229-236.

[5] LIU Wen, LI Min, BAI Xiang-zhong et al. Deformation calculating of electromagnetic launcher’s rail subjected to logarithmic magnetic pressure[J]. Modern Applied Science，2010,4(8): 127-133.