时变噪声统计估计的自适应UKF目标跟踪算法
2013-11-23黄长强李美亚齐晓林
蔡 佳,黄长强,李美亚,齐晓林
(1.空军工程大学, 陕西 西安 710038;2.西安机电信息研究所, 陕西 西安 710056)
目标跟踪是为了维持对目标当前状态的估计,同时也是对传感器接收到的量测信息进行处理的过程[1]。但是,传感器的测量方程很多都是非线性的,需要采用非线性的估计方法。扩展卡尔曼滤波(Extended Kalman Filtering,EKF)算法是一种常用的方法[2-4],但它有两点缺陷:必须满足小扰动假设,只适合弱非线性系统,对于强非线性系统,滤波性能极不稳定,甚至发散;需要计算Jacobian矩阵,计算复杂,容易出错。
Julier和Wan等人提出了基于U变换的无迹卡尔曼滤波算法[5-7]。UKF不是像EKF那样去近似非线性模型,而是对后验概率密度函数进行近似以得到次优的滤波算法,具有不需求导,估计精度高等优点。然而,UKF算法需要知道系统模型参数和噪声统计特性等先验知识。如果先验知识未知或不准确,滤波器将会产生较大的估计误差,甚至造成滤波发散。传统做法是将未知的噪声统计特性假设为1组均值为0、协方差已知的高斯白噪声序列,但是零均值假设并不适于处理目标持续机动的情形,最终造成滤波发散。
为此,本文设计了一种非零均值的时变噪声统计估计器,引入含有自适应衰减因子的加权系数,将时变噪声统计估计与传统UKF算法相结合形成一种自适应滤波(Adaptive UKF,AUKF)算法。
1 非零均值UKF算法
UKF规定一组确定性的σ点,当状态向量的概率密度函数是高斯型时,利用这组σ点获取高斯密度函数的真正均值和协方差,当高斯型状态向量的概率密度函数经由非线性系统进行传递时,对任何一种非线性系统,利用这组σ点能获取精确到二阶的后验均值和协方差。
假设非线性离散系统的状态方程和测量方程为:
Xk=f(Xk-1,k-1)+wk-1
(1)
Zk=h(Xk,k)+vk
(2)
式中,过程噪声wk与测量噪声vk均为零均值高斯白噪声序列,分别具有协方差阵:cov(wk,wl)=Qkδkl,cov(vk,vl)=Rkδkl。初始状态X0的统计特性为EX0=x0,varX0=P0,且X0、wk和vk互不相关。
传统UKF算法[8-10]通常假定过程噪声和测量噪声均值为零,然而在实际情况中,噪声零均值的条件并不能够满足,因此首先要对非线性系统进行修正:
Xk=f(Xk-1,k-1)+wk-1+q
(3)
Zk=h(Xk,k)+vk+r
(4)
式中,q和r分别为状态方程和测量方程的附加噪声均值,E(wk-1+q)=q,E(vk+r)=r。
当噪声均值非零时,同样需要对传统UKF算法进行修正,具体步骤如下:
(5)


(χk/k-1)i=f((χk-1/k-1)i)+q,i=0,1,2,…,2L
(6)
(7)
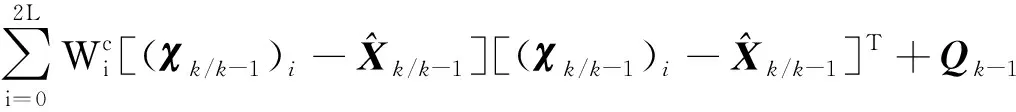
(8)


(Zk/k-1)i=h((χk/k-1)i)+r,i=0,1,…,2L
(9)
(10)
(11)
(12)
式中,Rk为测量噪声协方差矩阵。

(13)
(14)
(15)
2 时变噪声统计估计的AUKF算法
2.1 噪声统计估计器
基于极大后验估计原理[11]和测量值Zk,根据参考文献[12-13],得到如下次优MAP噪声统计估计器:
(16)
(17)
(18)
(19)

上述MAP估计器是针对时变的噪声统计特性,定常时的噪声统计估计比较简单,且估计值已被证明为无偏的[14]。本文考虑时变噪声统计特性。
(20)
式中,b为遗忘因子,0 将上述时变噪声统计的估计值代入传统UKF,即可得到改进的自适应UKF算法,计算流程如下: (21) (22) (23) (24) (25) (26) (27) (28) 由于过程噪声可以经过建模进行补偿,对模型变化的影响不是很大;而测量噪声主要是由工作环境引起的,其不确定性很大,不能进行建模补偿。因此,实际工作中系统模型的变化主要是由测量噪声引起的。本文仅对测量噪声的均值r和方差阵R进行估计,暂不考虑过程噪声的影响。 为了验证本文设计的自适应UKF算法性能,首先做出以下假设: 1)状态方程线性,测量方程非线性。 2)过程噪声统计特性:均值q=0,方差为Q;测量噪声统计特性:均值r≠0,方差为R。 根据以上假设条件,则系统模型为: Xk=Φk,k-1Xk-1+wk-1 (29) Zk=h(Xk,k)+vk+r (30) 初始状态设为:x0=[1 000 3 000 20 50 3 -4]T,P0=diag[100 100 1 1 0.1 0.1]。 时变噪声的初始统计特性为: Q0=diag[1 1 0.120.120.0120.012], 采样时间0.1 s,仿真时间100 s,对本文提出的AUKF算法进行100次Monte Carlo仿真实验。 仿真结果的评价指标选为状态向量的均方根误差(RMSE),定义为: (31) AUKF算法的跟踪效果如图1所示,可见估计值与目标的真实轨迹基本重合,这说明采用本文的自适应滤波算法可以实现对目标的有效跟踪。 图2~4所示为AUKF算法的滤波结果及与EKF算法和传统UKF算法的误差比较。 图2至图4所示为笛卡尔坐标系下,目标在x和y方向的位置、速度和加速度均方根误差比较。从仿真结果图对比看出,EKF算法和传统UKF 算法的状态估计结果均不及AUKF,尤其是EKF算法的均方根误差更大,这是因为EKF本身忽略了高阶截断误差,对噪声统计特性估计不准确造成的。本文提出的AUKF 算法可以不断地实时估计时变噪声的统计特性,根据量测信息对滤波发散趋势进行判断,并引入指数加权的衰减因子抑制滤波发散,因此能够有效地解决由于噪声统计特性未知或不准确而引起的滤波精度不高的问题,大大提高了收敛速度和估计精度。 表1 结合本文选取的评价指标-状态向量各个元素的均方根误差,比较了3种算法的滤波性能。仿真结果表明,AUKF 算法在滤波精度方面明显优于EKF算法和传统UKF算法,因此,状态估计也更接近于真实状态,目标跟踪性能更优。 表1 算法性能比较(均方根误差) 对于目标跟踪问题,传统UKF算法在噪声先验知识未知时将其均值假设为零,这种处理方法容易造成滤波发散。为此,本文在对系统模型和传统滤波算法修正的同时,设计了一种时变噪声统计估计器,并将其引入到传统UKF算法当中,提出了一种自适应UKF算法,该算法可以在滤波计算的同时,对噪声的未知先验信息进行实时统计估计和修正。仿真结果表明,该算法在保证滤波收敛的同时提高了跟踪精度。 [1] 韩崇昭, 朱洪艳, 段战胜. 多源信息融合[M]. 北京: 清华大学出版社, 2006: 124-188. HAN Chong-zhao, ZHU Hong-yan, DUAN Zhan-sheng. Multi-source information fusion[M]. Beijing: Tsinghua University Press, 2006: 124-188. (in Chinese) [2] EINICKE G A, WHITE L B. Robust extended Kalman filtering[J]. IEEE Transactions on Signal Processing, 1999, 47(9): 2596-2599. [3] 秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安: 西北工业大学出版社, 1998: 182-188. QIN Yong-yuan, ZHANG Hong-yue, WANG Shu-hua. Kalman filtering and integrated navigation theory[M]. Xi’an: Northwestern Polytechnical University Press, 1998: 182-188. (in Chinese) [4] JOSEPH J, LAVIOLA Jr. A comparison of unscented and extended Kalman filtering for estimating quaternion motion[C]//Proceedings of the American Control Conference. Denver:[s.n.],2003: 2435-2440. [5] JULIER S J. The scaled unscented transformation[C]//Proceedings of the American Control Conference.Anchorage:[s.n.],2002: 4555-4559. [6] JULIER S J, UHLMANN J K. Unscented filtering and nonlinear estimation[J].Proceedings of the IEEE, 2004, 92(3): 401-422. [7] WAN E A, VAN DER MERVE R. The unscented Kalman filter for nonlinear estimation[C]//Proceedings of the IEEE Adaptive Systems for Signal Processing, Communication and Control Symposium.Lake Louise:[s.n.],2000:153-158. [8] 杨凯, 倪龙强, 张丽华, 等. 基于IMM-UKF的非线性机动目标跟踪仿真研究[J]. 火炮发射与控制学报, 2010(3): 12-16. YAN Kai, NI Long-qiang, ZHANG Li-hua, et al. Study on tracking simulation of nonlinear maneuvering target based on IMM-UKF[J]. Journal of Gun Launch & Control, 2010(3): 12-16. (in Chinese) [9] 江宝安, 万群. 基于UKF-IMM的双红外机动目标跟踪算法[J]. 系统工程与电子技术, 2008,30(8):1454-1459. JIANG Bao-an, WAN Qun. Maneuvering target passive tracking with dual infrared observers using IMM algorithm based on UKF[J]. Systems Engineering and Electronics, 2008, 30(8): 1454-1459. (in Chinese) [10] 张文玲, 朱明清, 陈宗海. 基于强跟踪UKF的自适应SLAM算法[J]. 机器人, 2010, 32(2): 190-195. ZHANG Wen-ling, ZHU Ming-qing, CHEN Zong-hai. An adaptive SLAM algorithm based on strong tracking UKF[J]. Robot, 2010, 32(2): 190-195. (in Chinese) [11] SAGE A P, HUSA G W. Adaptive filtering with unknown prior statistics[C].Tokyo: Proceedings of the Joint Automatic Control Conference, 1969, 760-769. [12] 石勇, 韩崇昭. 自适应UKF算法在目标跟踪中的应用[J]. 自动化学报, 2011, 37(6): 755-759. SHI Yong, HAN Chong-zhao. Adaptive UKF method with applications to target tracking[J]. Acta Automatica Sinica, 2011, 37(6): 755-759. (in Chinese) [13] 孙尧, 张强, 万磊. 基于自适应UKF算法的小型水下机器人导航系统[J]. 自动化学报, 2011,37(3):342-353. SUN Yao, ZHANG Qiang, WAN Lei. Small autonomous underwater vehicle navigation system based on adaptive UKF algorithm[J]. Acta Automatica Sinica, 2011, 37(3): 342-353. (in Chinese) [14] 赵琳, 王小旭, 薛红香, 等. 带噪声统计估计器的Unscented卡尔曼滤波器设计[J]. 控制与决策, 2009, 24(10): 1483-1488. ZHAO Lin, WANG Xiao-xu, XUE Hong-xiang, et al. Design of unscented Kalman filter with noise statistic estimator[J]. Control and Decision, 2009, 24(10): 1483-1488. (in Chinese)2.2 自适应UKF算法
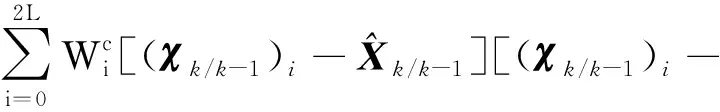

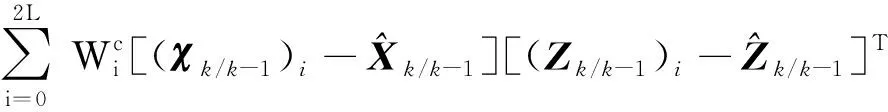
3 仿真分析
3.1 参数设置
3.2 结果分析






4 结束语
