舰艇摇摆对小口径舰炮射击精度的影响分析

张龙杰,谢晓方,孙 涛,李德栋

(海军航空工程学院 兵器科学与技术系, 山东 烟台 264001)

舰艇摇摆误差是舰载武器特有的误差，小口径舰炮对空作战过程中，为了消除舰艇摇摆引起的射击线偏移，惯导系统要实时测量舰艇的摇摆姿态，在此基础上利用稳定控制系统进行反向补偿[1-3]，从而实现舰炮对目标的稳定跟踪和射击。

在舰艇摇摆姿态的测量过程中，惯导系统会引入测量误差，同时在舰艇摇摆姿态反向补偿过程中，由于稳定控制系统存在动力学环节，必然会导致补偿值与真实值之间存在误差，这里统一将测量误差和补偿误差称为舰艇摇摆误差。

为了对舰艇摇摆误差进行分析，论文首先建立了长峰波海浪的运动模型，以海浪的运动作为输入激励舰艇的摇摆，在此基础上建立了舰炮对空射击的误差传递模型，最后选取典型海况，对舰艇摇摆造成的舰炮射击误差进行了仿真研究，并给出了相关结论和建议。

1 坐标系定义

1) 舰艇惯性坐标系Wxiyizi。舰艇惯性坐标系的原点W位于静水面下舰艇的摇摆中心点位置，Wxi轴沿静水面下舰艇纵轴指向舰艏，Wzi轴沿-g方向指向天向，Wyi轴通过右手定则确定。

2) 舰艇甲板坐标系Wxwywzw。舰艇甲板坐标系的原点W位于舰艇的摇摆中心点位置，Wxw轴沿船体纵轴指向舰艏，Wzw轴垂直于甲板平面向上，Wyw轴通过右手定则确定。

3) 舰炮坐标系Cxjyjzj。舰炮坐标系的原点C位于炮管回转中心点的位置，各坐标轴与舰艇甲板坐标系对应的坐标轴平行。

2 舰艇在海浪中的摇摆运动

2.1 舰艇摇摆运动的系统传递函数

舰艇在海浪上的各种摇摆运动中，横摇φ(t)和纵摇θ(t)运动对舰载武器的发射影响最大[4]，其摇摆方程[5]可以统一表示为：

(1)

式中：c(t)表示舰艇的摇摆运动；ν为衰减系数；ωt为舰艇固有圆振荡频率。

将舰艇视作一个线性变换系统S0，r(t)为输入，c(t)为输出，对于式(1)，给定系统S0的脉冲响应函数h(t)，必有：

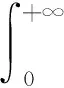
对上式进行傅里叶变换，得到：

C(ω)=H(ω)R(ω)

(2)

式中：C(ω),H(ω)和R(ω)分别为c(t),h(t)以及r(t)的傅里叶变换。

在频域，舰艇运动的谱函数Sc(ω)=C(ω)C*(ω)，波能谱函数Sr(ω)=R(ω)R*(ω)，结合式(2)得到：

Sc(ω)=|H(ω)|2Sr(ω)

(3)

由式(1)，系统脉冲响应函数h(t)满足方程：

对上式进行拉氏变换，得到：

(4)

为了求解H(ω)，令s=jω，由式(4)得到舰艇摇摆运动的频率响应函数：

(5)

式(5)对应的幅频传递函数为：

(6)

相频传递函数为：

(7)

式中，Λ=ω/ωt为相对频率，μ=ν/ωt为无因次衰减系数。

2.2 海浪波幅运动模型

为了得到海浪波倾角输入r(t)，先求解海浪的波幅输入ζ(t)。为此，采用国家海洋局倡导的我国沿海波能谱公式[5]：

(8)

式中：ω为波浪频率；U=6.28(h1/3)0.5为风速，h1/3为有义波高。根据波能谱的定义[5]，频率在ω～(ω+Δω)之间的海浪波谱密度函数为：

式中：ζω为频率在ω～(ω+Δω)之间的规则波的波幅。当Δω→0时，ω～(ω+Δω)之间的规则波趋于确定频率的谐波，由此得到频率位于ω～(ω+Δω)之间的单元规则波的等效波幅ζω与波能谱的关系为：

(9)

海浪的波能谱属于狭带谱，绝大部分能量集中于某一窄带内，假设为ωa～ωb。采用频率等分法分析海浪的运动，对于给定的频率采样步长Δω，样本总数Nω=(ωb-ωa)/Δω，对于第k(k=1,2,…,Nω)个样本，频率ωk=ωa+kΔω，对应的波幅运动方程为：

ζωk(t)=[2Sr(ωk)·Δω]0.5cos(ωkt+φk)

式中：φk为[0,2π)区间内均匀分布的随机数。从而得到海浪运动模型：

(10)

2.3 舰艇摇摆运动模型

舰艇在波浪中运动时，需要以遭遇频率分析舰艇的摇摆。设舰艇T以航速vt在波长为λ速度为vc的海浪中航行，如图1所示。

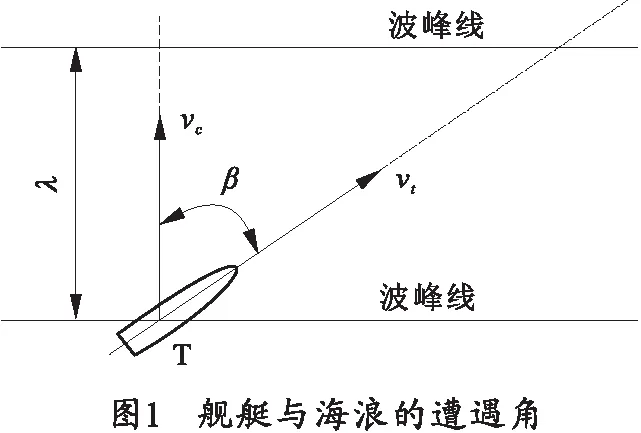
图1中：β为舰艇与海浪的速度夹角。由图1得到舰艇与海浪的遭遇频率：

(11)

由于波能谱的大小与表示频率无关，即：

SR(ωe)dωe=Sr(ω)dω

(12)

对式(11)微分，代入式(12)中，得到考虑遭遇频率后的海浪波能谱：

(13)

如2.1节所述，分析舰艇摇摆运动时，输入r(t)是海浪的波倾角运动，因此需要把波幅运动输入ζ(t)转换成r(t)，考虑遭遇频率ωe后，以kωe表示频率为ωe的波数，根据波倾角与波幅的关系有：

(14)

对于不同的摇摆运动，χ为考虑了动水压力以及船长和船宽影响后的修正系数，参考式(9)，得到波倾角谱密度函数：

(15)

对于由频率等分法得到的第k(k=1,2,…,Nω)个样本，对应的遭遇频率ωe k，参考式(9)，考虑遭遇频率后的波幅为：

ζωe k=[2SR(ωe k)·Δωe k]0.5

(16)

式中：Δωe k=ωe k-ωe(k-1)可利用式(11)求解。由式(14)和(16)得到考虑遭遇频率后的波倾角样本：

从而得到以波倾角表示的海浪运动模型：

(17)

由式(3)和式(15)，在分段频率ωe k处舰艇运动的谱密度函数为：

Sc k(ωe k)=|H(ωe k)|2Sα k(ωe k)

从而得到舰艇在该频段的运动方程样本：

cωe k(t)=[2Sck(ωe k)·Δωe k]0.5cos[ωe kt+φe k]

式中：φe k=φk+φ(ωe k)，φ(ωe k)为系统的相频函数，通过式(7)求解。由此得到舰艇摇摆模型：

(18)

3 舰炮射击误差

3.1 舰艇摇摆误差分析

舰艇摇摆误差主要包括舰艇摇摆的观测误差em(φm,θm)和稳定系统的补偿误差ec(φc,θc)。

对于补偿误差，以横摇运动为例，由于舰炮稳定系统存在动力学环节，舰艇横摇角的输出值φm与理想值φw之间会存在一定误差，为此考虑一阶稳定系统控制环节，对应的标准传递函数为:

Φc/Φi=1/(Tφs+1)

式中：Tφ为横摇稳定系统时间延迟常数。一阶控制环节对应的控制结构如图2所示。

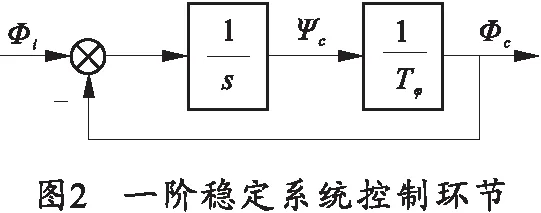
由图2得到求解一阶控制环节的微分方程

(19)

式中：ψc,φi和φc依次为Ψc,Φi和Φc的拉氏反变换。一般情况下，观测误差em(φm,θm)服从正态分布，φm和θm为观测误差的均方值，而补偿误差φc和θc为解算值，因此舰艇整体摇摆误差服从:

对应的抽样算法为：

e(φc,θe)=(φc+u1φm,θc+u2θm)

(20)

式中：u1～u2为服从N(0,1)分布的随机数。

3.2 舰炮对空射击误差

舰艇摇摆误差是在舰艇惯性坐标系的基础上引入的，无法将其直接引入到舰炮的对空射击误差中，即方位角方向和高低角方向的误差，为此需要进行一定的数据处理。

在舰艇惯性坐标系下，以φw1和θw1表示舰艇的真实摇摆角，φw2和θw2为含有误差的摇摆角，则有:

舰艇惯性坐标系与甲板坐标系的空间转换关系如图3所示。

假设目标提前点在舰艇惯性坐标系Wxiyizi下的坐标为Pi=[xiyizi]T，在甲板坐标系Wxwywzw下的坐标为Pw=[xwywzw]T，则有：

Pw=Mw i(φw,θw)Pi

(21)

式中：

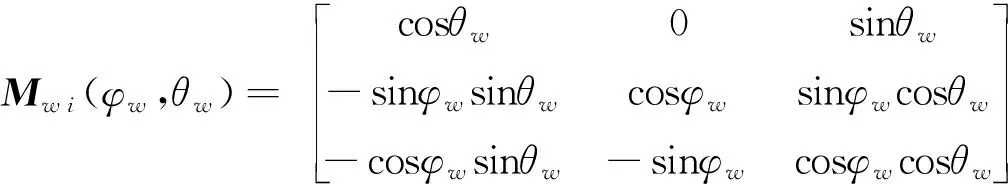
Pju=Mw i(φw u,θw u)Pi-P0

(22)

式中：P0=[lxlylz]T为舰炮回转中心在甲板坐标系下的坐标；u=1和u=2分别表示目标提前点在舰炮坐标系下的解算坐标和实际坐标，这里解算坐标指无误差情况下的值，实际坐标指引入误差后的值。为了求取舰炮射击误差，将目标提前点在舰炮坐标系下的直角坐标转换为球坐标，在式(22)的基础上有：

(23)

式中：γju和φju分别为目标未来点在舰炮坐标系下方位角和高低角的解算值和实际值。则由于舰艇摇摆引起的方位角和高低角方向的射击误差为：

(24)

4 仿真与分析

小口径舰炮大多装备于大中型舰艇中，以驱逐舰为例，其最大作战海况一般不高于5级，为对比分析，分别选取3级(轻浪)和5级(大浪)海况进行研究。取波能谱有效频率ωa=0.05 rad，ωb=4 rad，频率采样步长Δω=0.05 rad，仿真时间t=100 s，步长0.05 s，对于3级海况，取h1/3=1 m，对于5级海况，取h1/3=3.5 m，参考国家海洋局提出的我国沿海波能谱，由式(10)得到不同海况下的海浪模型，如图4所示。

图4(a)和4(b)分别为3级和5级海况下的海浪模型，从整体上看，3级海况时海浪的波动幅度较小，频率较高，5级海况时海浪的振幅较大，频率较低，符合实际情况，并且二者的波动幅度与给定的有义浪高相吻合，表明了海浪建模方法是可信的。

对于带舭龙骨的驱逐舰，通过文献[5]～[7]，舰艇横摇无因次衰减系数一般在0.05～0.075之间，纵摇无因次衰减系数一般在0.3～0.5之间，横摇周期在9～9.5 s之间，纵摇周期在4～5.5 s之间。以下标φ表示横摇运动参数，下标θ表示纵摇运动参数，取χφ=0.5，μφ=0.06，ωφ=2π/9，χθ=0.15，μφ=0.5，ωθ=2π/5，β=5π/4，vt=9.26 m/s(18节)，由式(18)得到艏斜浪下舰艇的横摇和纵摇运动，如图5所示，限于篇幅，这里只给出了5级海况下舰艇的摇摆运动。

图5(a)和5(b)分别为5级海况下舰艇的横摇和纵摇运动，可以看出，舰艇的横摇幅度要高于纵摇幅度，并且横摇周期也要比纵摇周期大。

图6给出的是5级海况下，由式(19)计算得到的稳定系统的补偿误差，这里取Pi=[800 600 20]Tm，P0=[30 0 5]Tm，Tφ=0.03。舰艇摇摆的测量误差相当于零均值的高斯白噪声，这里不再单独对其进行仿真。图6(a)和6(b)分别对应舰艇的横摇和纵摇误差。可以看出，舰艇横摇误差要高于纵摇误差。

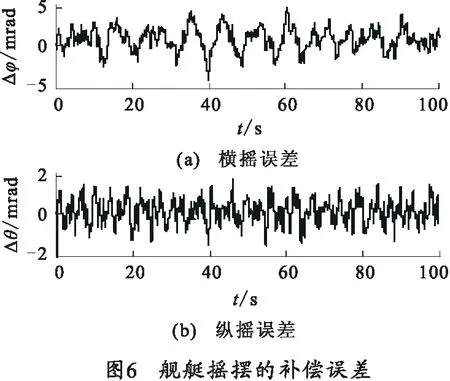
由式(23)和式(24)计算舰艇摇摆引起的舰炮对空射击误差，图7和图8分别为3级和5级海况下的计算结果。图7(a)和图8(a)为舰炮的方位角射击误差，图7(b)和图8(b)为舰炮的高低角射击误差。

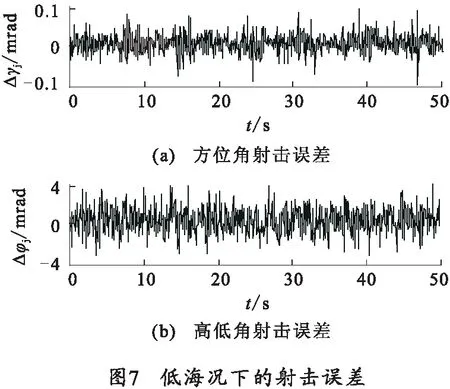
综合分析图4～图8，海况越高海浪运动越剧烈，舰艇摇摆幅度越大，引起的摇摆误差也越高，舰炮射击误差也越大。另外，舰艇的横摇幅度要明显高于纵摇幅度，横摇误差也要高于纵摇误差，但是对于舰炮而言，高低角方向的射击误差却要明显高于方位角方向的射击误差，这是由于小角度转动下，高低角方向的射击误差主要取决于舰艇的横摇和纵摇运动，方位角方向的射击误差主要取决于舰艇的艏摇运动，由于艏摇运动很小，基本可以忽略，所以舰炮在方位角方向的射击误差很小。

5 结 论

本文分析了舰艇摇摆对小口径舰炮射击精度的影响，结果表明：

1) 舰艇横摇角误差要高于纵摇角误差，因此在减摇设计中要首先考虑降低舰艇的横摇运动。

2) 海况越差时，舰炮射击误差越高，因此为了提高对空作战效能，要尽量在低海况环境下作战，并选择合适的航向和航速来降低舰艇的摇摆。

3) 舰炮在方位角方向的射击误差很小，并远远低于高低角方向的射击误差，对于拦截小航路捷径掠海飞行的反舰导弹，由于弹体在舰炮高低角方向的受弹投影长度较短，拦截概率会有所降低。

[1] 毛征, 雷加印, 吕春花, 等. 自行高炮射击线稳定性分析[J]. 火炮发射与控制学报, 2011(3): 92-96.

MAO ZHeng,LEI Jia-yin,LV Chun-hua,et al.Analysis on firing line satbility of SPAA gun[J].Journal of Gun Launch & Control,2011(3):92-96.(in Chinese)

[2] 陈机林, 杜新妮. 舰载火箭炮消摇摆稳定系统控制器设计[J]. 火炮发射与控制学报, 2005(1):43-46.

CHEN Ji-lin, DU Xin-ni. Design of stabilization system controller for swing elimination of ship-board rocket gun[J]. Journal of Gun Launch & Control, 2005(1):43-46. (in Chinese)

[3] 何永昌,王雷,韩昭旺.基于舰体坐标系的瞄准线与火力线稳定模型[J].火炮发射与控制学报,2009(2):24-27.

HE Yong-chang, WANG Lei, HAN Zhao-wang. Stabilization model of line of sight and axis of firepower based on warship coordinate system[J]. Journal of Gun Launch & Control, 2009(2): 24-27. (in Chinese)

[4] 戴耀, 汪德虎. 舰艇运动对舰炮起始发射条件的影响[J]. 火炮发射与控制学报, 2002(3): 9-12.

DAI Yao, WANG De-hu. Influence of warship motion to naval gun initiative shoot condition[J]. Journal of Gun Launch & Control, 2002(3): 9-12. (in Chinese)

[5] 李积德.船舶耐波性[M]. 哈尔滨：哈尔滨工程大学出版社, 2007：33-76.

LI Ji-de. Ship seakeeping[M]. Harbin：Harbin Engineering University Press, 2007：33-76. (in Chinese)

[6] 盛振邦, 刘应中. 船舶原理(下册)[M]. 上海: 上海交通大学出版社, 2004: 338-449.

SHENG Zhen-bang, LIU Ying-zhong. Ship theory (Volume two)[M]. Shanghai: Shanghai Jiao Tong University Press, 2004: 338-449. (in Chinese)

[7] 邢耀国, 曲凯,许俊松,等.舰船摇摆条件下固体火箭发动机舰载寿命预估[J]. 推进技术, 2011, 32(1):32-35.

XING Yao-guo, QU Kai, XU Jun-song, et al. Life prediction of shipborne solid rocket motor under the ship swing motion[J]. Journal of Propulsion Technology, 2011, 32(1): 32-35. (in Chinese)