基于可测电气量鼠笼式异步电机能效在线监测方法
2013-11-22张蓬鹤赵海森刘晓芳杜中兰
王 庆,张蓬鹤,赵海森,刘晓芳,杜中兰
(1.华北电力大学,北京102206;2.中国电力科学研究院,北京100192)
0 引 言
电机系统能效评估中,最重要的一个环节就是电机运行效率的在线评估,即利用电机输入功率和输出机械功率求出电机实时运行效率。对于输入功率,可以直接利用测量电机的机端三相电压和电流求得;对转子轴输出机械功率,只需求出转子侧的输出转矩与转速即可,但是,由于在实际生产中大多数场合,电机转子侧并没有安装转矩和转速测量装置,导致输出功率无法直接测量,只能通过输出转矩和转速的在线监测间接估算电机输出功率,因此研究转速和输出转矩的辨识方法具有重要意义。
传统电机效率辨识方法有铭牌法、转差率法、电流法、损耗分析法等[1-2]。由于电机实际效率随负载变化而变化,尤其对于小功率、多极数电机,其效率变化很大,所以铭牌法并不能代表电机实际运行效率;转差率法是假定电机负载与额定负载比例正比于转差率与额定负载时转差率的比值,这种方法也存在辨识误差较大的问题;电流法即假定负载率正比于定子绕组电流与额定电流比值,由于实测电流中含有空载电流,会导致效率辨识产生较大误差;损耗分析法要求获得电机各项损耗,而在现场很难获得这些数据,只能结合一些经验数据。
以上方法进行能效在线辨识时均在不同程度存在一定误差,能够准确获得电机运行能效的途径是测出电机转速和转矩,进而计算出输出功率及运行效率。在这方面研究较多的是转速辨识方法,例如文献[3]提出电机转速自适应辨识方法,解决了传统MARS 算法中忽略磁链观测误差的问题;文献[4]提出基于扩展卡尔曼滤波器的电机转速估算方法,选取定子磁链、转速、转子位置为状态变量,对电机转速进行估算;文献[5]提出无速度传感器矢量控制原理,采用遗传算法进行转速辨识。在转矩辨识研究方面,文献[6]以滑模状态观测器为基础,分析了转矩观测值受电感参数偏差的影响程度,之后利用Layapunov 稳定性理论,设计了基于自适应率的电感参数辨识方法;文献[7]提出采用联级BP 神经网络对负载转矩进行估算的方法;文献[8-9]提出离线测量电机反电势系数,根据转子位置与转速,查表计算得到反电势值,进而完成转矩计算。上述辨识方法大多依赖于电机数学模型,由于电机参数具有时变非线性特点,导致转速、转矩估计准确性随运行状态变化较大。
为了实现基于可测电气量的鼠笼式异步电机能效在线评估,本文首先通过估算负载转差率得出转子槽频率范围,进一步对定子电流进行快速傅里叶分析,得出能够反映电机转速的精确转子槽频率,上述处理方法解决了转子槽谐波与齿谐波混叠的问题,能够准确辨识电机实时转速;其次再利用实测电压、电流计算绕组磁链,进而得出电机气隙转矩及输出转矩;最后利用辨识得到的电机转速、转矩,求取输出功率,进而得出电机的运行效率。
1 鼠笼式异步电动机能效测试方法
1.1 基于转子槽谐波的转速辨识理论
由于定转子开槽导致气隙不均匀,定子绕组通入三相对称电流时的气隙磁势[10-11]:
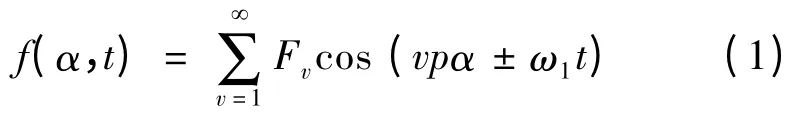
式中:α 为机械角度;ω1为电流角频率;p 为极对数;ν 为谐波次数,当v = 6k + 1(k 为正整数)时,谐波磁势正转;当v = 6k-1 时谐波磁势反转。
当定转子开槽后,气隙磁导可表示为[14]:
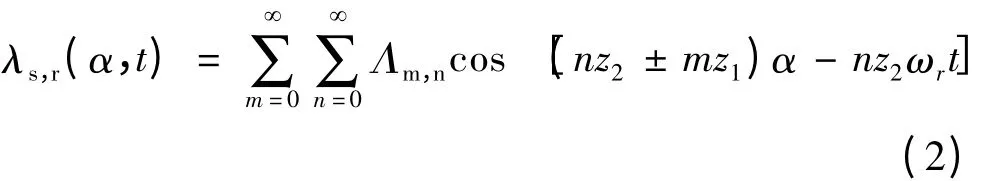
式中:z1为定子槽数;z2为转子槽数;ωr为转子旋转角速度。
进而可得定转子开槽后的电机气隙密度:

式中:μ0为磁导率。
由上式可以看出,定子齿谐波磁场在定子绕组中感生的电动势频率均为基波频率,转子绕组电流产生的齿谐波磁场在定子绕组中感生谐波电动势,进而产生相应频率电流,该电流频率与转子转速直接相关,这种与转子转速相关的特定频率谐波即为转子槽谐波,其频率可表示:
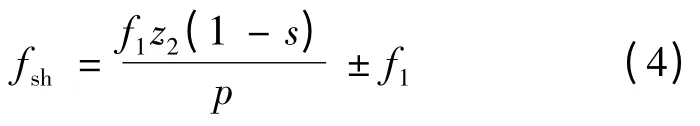
式中:s 为转差率;f1为电网频率。
由上式可知,利用电动机转子槽频率,可以求得转差率,进而得出电机转速如下:
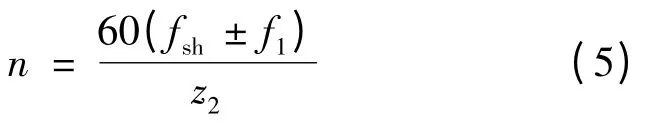
综上,可先利用快速傅里叶变换对定子电流进行频谱分析,从中提取出转子槽谐波频率,进而得出电机转速。
1.2 气隙转矩法
在估算输出转矩的过程中,首先测试输入端电压和电流,得出电机瞬时输入功率[12-13]P1:

式中:

式中:ua、ub、uc为相电压;ia、ib、ic为相电流;ψa、ψb、ψc分别为a、b、c 绕组磁链,r 为绕组电阻。
将式(7)代入式(6)中可得:
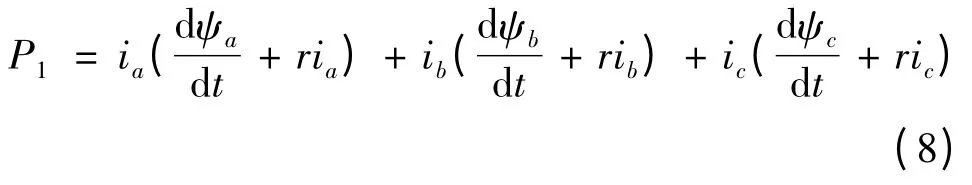
其中输入功率减去铁耗和铜耗等项后可得气隙转矩方程式如下:

式中:iA、iB、iC为线电流;uCA、uAB为线电压;R 为1 /2线间电阻值,当绕组为星型连接时R = r;当绕组为角接时R = r/3;p 为极对数;n0为同步转速;pfe为铁耗。
通过以上分析可知,将气隙转矩减去机械损耗和负载杂耗所对应转矩即可求出电机输出转矩。
2 转矩和转速辨识过程中的问题及解决方法
2.1 转子槽频率与齿谐波混叠
2.1.1 问题描述
由电机基本理论可知,定子绕组电流产生的基波磁势,受饱和因素影响,会产生一系列同步速旋转的谐波磁场,其在定子绕组中感应出谐波次数与其极对数相同的谐波电势,进而产生相应频率电流。对于某些特殊槽配合,转子槽频率与上述谐波频率容易出现混叠现象,导致转子槽频率难以直接辨识。以一台0.75 kW、6 极电机为例,其定转子槽数分别为36 和33,定子绕组中存在着11 次齿谐波电势及电流,而转子电流产生齿谐波磁势在同步速时,在定子绕组中感应的电流频率也为11 次,这两种频率在一些特殊转速下非常接近,发生混叠现象,如图1 所示,这将导致转速辨识出现较大误差。
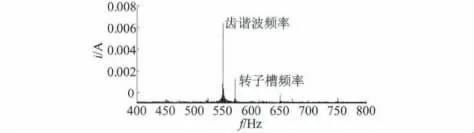
图1 定子电流频谱
2.1.2 解决方法
先估算负载转差率得出转子槽频率范围,再对定子电流进行快速傅里叶分析,得出转子槽频率,该方法可解决转子槽谐波与齿谐波混叠的问题,实现电动机转子槽频率的精确辨识。负载率可根据电机输入功率P1、空载及额定参数得出:

式中:ΔPN为额定负载时损耗;ΔP0为空载损耗;n0为同步速;nN为额定转速;λ 为负载率估算值,sλ为转差率估算值。
利用式(10)~式(11)估算出电机负载转差率sλ,通过式(4)求出转子槽频率估算值。然后判断所求的转子槽频率估算值是否在电机转子槽频率变化范围之内。其中转子槽频率变化范围是依据电机满载转速与空载转速估算出对应的转子槽频率区间。
仍以上述0.75 kW 电机为例,其转子槽变化范围为550.5~600 Hz。当输入功率为757 W 时,根据上述方法可得出电机转差率估算值为0.07,利用式(4)得出转子槽频率估算值为561.5 Hz,从而可知该估算值在转子槽变化范围之内,如图2 所示。从图中可以看出辨识得出准确的转子槽频率为571 Hz,进而得出转速为948.6 r/min。以此可解决转子槽谐波与齿谐波混叠时转速难以辨识的问题。

图2 定子电流频谱
2.2 气隙转矩中磁链的求解
2.2.1 问题描述
由式(9)可知,计算每个时刻的转矩需要求取两个积分,由上节推导可知,两个积分分别对应某两相绕组的磁链之差,即:
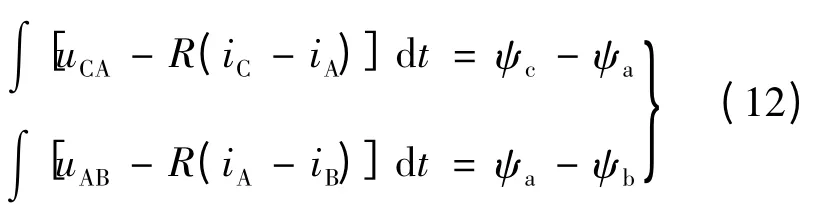
式中:ψa、ψb、ψc分别为a、b、c 绕组的磁链。上式的积分是定积分,即求取t 时刻转矩就要求取被积函数在[0,t]区间上的定积分。为了实时计算得出电机转矩,需对每个时刻求取定积分,计算量较大。
式(12)计算定积分需要知道三相绕组初始磁链,然而,所监测数据是从电动机稳定运行后开始记录,故所记录数据初始时刻的绕组磁链是不可以直接求得的。
2.2.2 解决方法
针对上述第一个问题,为方便叙述,令ψ = ψc-ψa。本文将t + Δt 时刻积分值转换成t 时刻两相绕组的磁链差ψ(t)与该时刻磁链差的增量Δψ(t)之和,此处Δt 为采样间隔时间,以为例,积分求解如下:
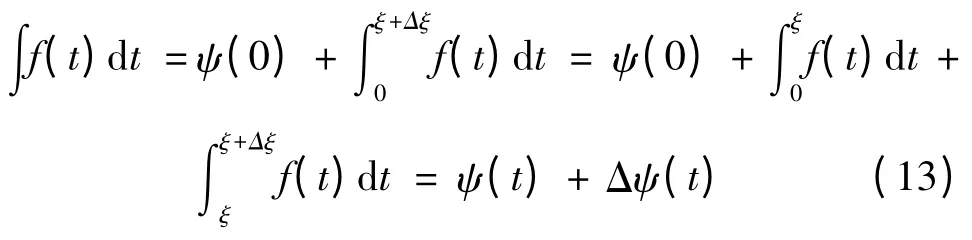
式中:f(t)= uCA-R(iC-iA),ψ(0)为A、C 两相绕组的初始磁链之差,ψ(t)为t 时刻A、C 两相绕组的磁链差。Δψ(t)为绕组磁链差ψ(t)在t 时刻的增量,可通过式(14)求解:

若已知ψ(0),利用每一时刻磁链差的增量Δψ,依次通过叠加求得每一时刻磁链差ψ,即积分。上述处理方法避免了重复求解定积分,大大减少计算量。
针对上述第二个问题,由于绕组初始时刻的磁链是未知的,则初始时刻的磁链差ψ(0)也是未知的并且不易求得,可转而求解其他某一时刻的ψ 或者确定ψ = 0 的时刻,这样即可利用每一时刻的增量Δψ 求得每一时刻的ψ。式(13)中f(t),理论上可以整理成一个正弦型函数解析式,积分后得到以t 为变量的余弦型函数解析式。对ψ 求微分,可得:

当Δt 足够小时,磁链差增量Δψ = dψ,则磁链差增量Δψ 是以t 为变量的正弦型函数解析式,二者角频率相同。由以上可知,ψ 与Δψ 在理论上相位相差最小的时刻所对应的ψ 值为零。
综上,求取气隙转矩中磁链的具体方法如下:首先求取每一采样时刻两相绕组磁链差的增量Δψ,找出第一个采样周期中Δψ 最小值及其所对应的时刻,且令该时刻的ψ 值为零。然后利用已知ψ 值与每一采样时刻的Δψ 依次叠加求得其它时刻的ψ。以一台5.5 kW、4 极满载电机为例,分别得到C 相、A 相绕组磁链差ψc-ψa和A 相、B 相绕组磁链差ψa-ψb的波形,如图3 所示。
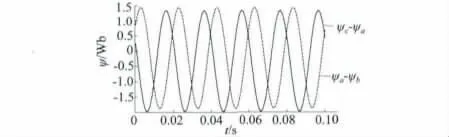
图3 磁链差的波形
然后利用式(9)求出每一时刻的气隙转矩,再找出转矩曲线中每个周期的最大值与最小值求其平均值,以此得到所需要辨识的气隙转矩。电动机气隙功率是跨过气隙传递到转子的功率,所以机械输出功率的计算可以转化为电机气隙转矩与机械损耗和杂散损耗的检测,从中减去机械损耗和负载杂耗所对应的转矩即可求出电机输出转矩。
2.3 数据采样频率及采样时间的选择
2.3.1 采样频率
电机机端电气量采样频率对转子槽频率辨识精度影响较大,即当电压电流采样频率设置不合理时,转子槽频率辨识误差较大。根据采样定理,要使离散信号在处理完毕后能够不失真地复现连续的模拟信号,采样频率fs必须与被采样信号宽带fm的关系为fs≥2fm,这时原信号频谱可以不发生明显畸变。经过对不同容量、不同槽配合电机进行大量实测验证,建议电气量采样频率fs>10 kHz。
2.3.2 采样时间
除采样频率外,采样时间也是影响辨识精度的重要因素。以一台定转子槽数为36 /32 的5.5 kW为例,当其输出转矩9 N·m、实测转速1 487.6 r/min 时,采样频率fs= 10 kHz 条件下,当采样时间0. 1 s 时,辨识转子槽频率840 Hz;采样时间0.2 s时,辨识转子槽频率845 Hz;两者辨识出的转速相差9.4 r/min。可见精确辨识需要足够的采样数据支持,但是采样时间过长会降低数据处理速度。通过大量实测对比,本文提出采样时间选择方法如下:根据同步转速估算转子槽频率fr,以此作为转子槽频率上限,在采样频率fs已知条件下,采样时间至少:t >
3 实验验证
针对一台Y132S-4、5.5 kW、定转子槽数为36 /32 的异步电机,对其在额定电压下不同负载时的转矩和转速进行辨识,通过辨识的转矩和转速在线求解输出功率。实验过程中电气量采样频率10 kHz,采样时间1 s。
3.1 满载时转速转矩辨识结果及实测对比
转速和转矩辨识结果如图4 所示。在该运行状况下的转子槽频率为820 Hz,据此可计算得出电机实时转速为1 443.75 r/min;计算得到的输出转矩平均值为36.72 N·m;利用转矩转速传感器测得的电机转速为1 445.78 r/min,输出转矩为36.5 N·m。可以看出,转速辨识精度较高,输出转矩误差为0.6%,基本满足工程需求。
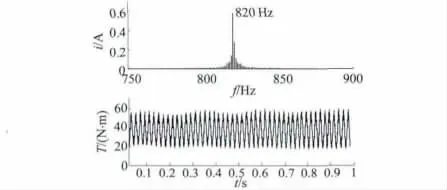
图4 额定负载时转子槽谐波频谱与转矩波形
3.2 75% 负载时的转速转矩辨识结果及实测对比
转速和转矩辨识结果如图5 所示。电机在该运行状况下的转子槽频率为828 Hz,据此可计算得出电机实时转速为1 458.75 r/min;计算得到的输出转矩平均值为26.37 N·m;利用转矩转速传感器测得的电机转速为1 459.21 r/min,输出转矩为26.3 N·m。可以看出转速辨识精度较高,输出转矩误差为0.3%。
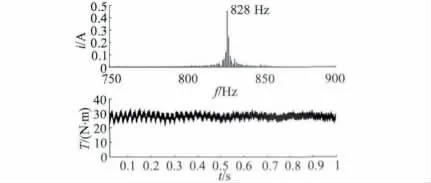
图5 75% 负载时转子槽谐波频谱与转矩波形
3.3 50% 负载时的转速转矩辨识结果及实测对比
转速和转矩辨识结果如图6 所示,电机在该运行状况下的转子槽频率为835 Hz,据此可计算得出电机实时转速为1 471.9 r/min;计算得到的转矩平均值为18.75 N·m;利用转矩转速传感器测得的电机转速为1 471.4 r/min,输出转矩为19.49 N·m。可以看出,转速辨识精度较高,输出转矩误差为3. 8%。
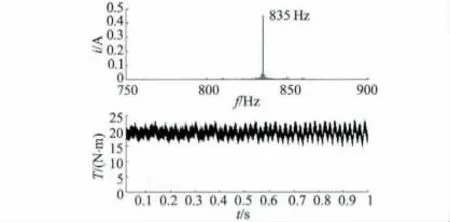
图6 50% 负载时转子槽谐波频谱与转矩波形
3.4 25% 负载时的转速转矩辨识结果及实测对比
转速转矩辨识结果如图7 所示。电机在该运行状况下转子槽频率为843 Hz,据此可计算得出电机实时转速为1 486.8 r/min;计算得到的输出转矩平均值为9.47 N·m;利用转矩转速传感器测得的电机转速为1 487.6 r/min,输出转矩为9.75 N·m。可以看出,转速辨识精度较高,输出转矩误差为2. 87%。
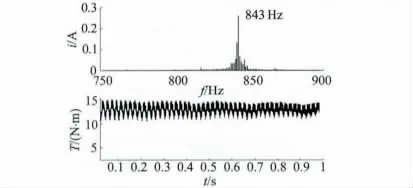
图7 25% 负载时转子槽谐波频谱与转矩波形
4 结 论
本文提出一种利用电动机可测电气量在线估算电动机运行效率的方法,通过对电机定子电流进行快速傅里叶变换得到转子槽频率,进而估算转速;再利用电机定子电压电流分析气隙转矩,然后估算输出转矩。利用辨识得到的转速、转矩可求出电机输出功率,从而得到电动机运行效率。
针对辨识转速中遇到的转子槽谐波与齿谐波混叠现象,通过电机转子槽谐波频谱结合负载转差率估算的转子槽频率范围对电机转速进行辨识;在气隙转矩法中通过对每一时刻磁链的求取避免了重复求解定积分,大大减少计算量,且解决了绕组初始磁链值未知的情况。
以一台5.5 kW 电机为例进行实验研究,对其不同负载时的转矩和转速辨识,结果表明转速辨识精度高,转矩误差在5% 以内,基本满足工程的要求。所研究的成果实现了基于电动机可测电气量对异步电机能效的在线辨识,为企业电机系统能效评估提供了重要技术支持。
[1] 秦和.电动机的能效水平及其影响[J].中小型电机,2003,30(1):1-13.
[2] 秦和.电动机效率测定方法的进展[J].中小型电机,2004,31(1):65-74.
[3] 胡楷,潘孟春,李圣怡,等.基于绝对稳定性的异步电机转速自适应辨识方法[J].控制与应用技术,2006,48(8):22-26.
[4] 张猛,肖曦,李永东.基于扩展卡尔曼滤波器的永磁同步电动机转速和磁链观测器[J].中国电机工程学报,2007,27(36):36-40.
[5] 应崇礼,赵继敏,李小海.基于遗传算法的感应电动机转速辨识[J].微特电机,2007,35(10):38-40.
[6] 郭鸿浩,周波,左广杰,等.无刷直流电机转矩观测与电感自适应辨识[J].中国电机工程学报,2011,31(33):151-158.
[7] 于红霞,姚莹,王向东.基于联级神经网络的电机转速和负载转矩辨识[J].电力电子技术,2011,45(4):58-60.
[8] Kang S J,Sul S K.Direct torque control of brushless DC motor with nonideal trapezoidal back EMF [J].IEEE Trans.on Power Electronics,1995,10(6):796-802.
[9] Liu Y,Zhu Z Q,Howe D.Direct torque control of brushless DC drives with reduced torque ripple[J].IEEE Transactions on Industry Applications,2005,41(2):599-608.
[10] Zhi Gao,Thomas G H.A sensoress rotor temperature estimator for induction machines based on a current harmonic spectra estimation scheme [J].IEEE Transactions on Industrial Electronics,2008,55(1):407-416.
[11] Kevin D H,Thomas G H.Sensorless speed measurement using current harmonic spectral estimation in induction machine drives[J].IEEE Transactions on Power Electronics,1996,11(1):10-15.
[12] John S H.Field test of motor efficiency and load changes through air-gap torque [J].IEEE Transactions on Energy Conversion,2003,10(3):477-483.
[13] John S H,Patrick L S.Field assessment of induction motor efficiency through air-gap torque [J].IEEE Transaction on Energy Conversion,1996,11(3):489-494.
[14] Heller B,Hamata V.异步电机中谐波磁场的作用[M].北京:机械工业出版社,1980.