永磁同步电动机矢量相位滞后的误差补偿控制

唐文明，骆光照，马升潘，张佳波

(西北工业大学，陕西西安710129)

0 引 言

永磁同步电动机用稀土永磁材料来建立磁场，使得电机体积小、结构紧凑、寿命长、维护方便、运行可靠且具有高效率、高功率密度等优良特性，因此，广泛应用到各种工业应用场合［1－4］。在永磁同步电动机伺服控制技术中，控制上存在的不可避免的时间延迟影响了永磁同步电动机矢量控制的实时性，造成控制矢量相位滞后。这种控制滞后现象在电机低转速时影响不大，但是当电机高转速运行时，会严重影响电机控制精度，甚至会造成系统振荡［5］。文献［6］对永磁同步电动机驱动系统硬件在环仿真过程中数字控制器与仿真器之间接口的不可避免时间延迟进行了分析，并未对永磁同步电动机矢量控制系统中控制上存在的时间延迟进行分析。为了避免控制滞后带来的转速精度不高或高速时电机振荡的问题，本文提出一种新型补偿控制算法，将相关补偿量引入到控制系统中，对滞后的空间电压矢量进行相位补偿，实现对电机近乎零滞后的控制，从而改善电机的控制特性。

在本文中，首先分析延迟产生的原因，对其滞后特性进行分析，然后在此基础上给出具体的补偿控制方法。为了验证补偿方法的有效性，最后进行仿真分析与实验验证。

1 永磁同步电动机矢量控制滞后特性分析与补偿方法

1.1 永磁同步电动机矢量控制系统

永磁同步电动机驱动系统是由DSP 控制器、电源逆变电路、永磁同步电动机(PMSM)以及传感器等几个部分组成，其系统结构图如图1 所示。DSP控制器采集传感器信号，其中包括A、B相电流、转子位置等，经过坐标变换、PI 调节等一系列控制过程后输出PWM 脉冲信号来驱动电源逆变器，电源逆变器根据数字控制器的PWM 信号将直流电源转换成永磁同步电动机的三相交流电。

图1 永磁同步电动机驱动系统结构图

在永磁同步电动机矢量控制系统中，控制系统输入参数，如A、B 相电流和电机转子位置，对于永磁同步电动机矢量控制来说是至关重要的，这些量的精确性及控制上的实时性都直接影响到控制系统的控制效果。

1.2 控制滞后机理分析

在矢量控制过程中，模拟量采集、矢量计算、PWM 输出时序如图2 所示。虽然占空比的计算已经完成，但PWM 的装载是在一个特定的时刻，比如下溢中断触发的时刻。这样，控制滞后是不可避免的。

图2 模拟量采集、矢量计算、PWM 输出时序图

根据图2 的分析，该控制滞后时间:

式中:TD为PWM 输出滞后时间;T0为电流、转子位置等参数采样时刻;T3为下个EV 下溢中断开始时刻。

1.3 控制滞后误差分析与补偿方法

永磁同步电动机的同步旋转坐标系参考定子坐标系dqs，以电机的同步转速旋转。由图3 可知，滞后时间TD导致两相旋转坐标系产生了一个大小为ωeTD的角度误差，这样会导致最终合成的输出空间电压矢量相位滞后。

图3 永磁同步电动机同步旋转坐标系物理模型图

在时域中，时间的延迟表示为x(t－TD)，转换到频域为e－jωTDX(jω)。根据上文的分析，控制器采样时刻为T0，PWM 作用时刻为T3，控制滞后的时间为T3－T0，即TD。在静止坐标系下，T0时刻定子电压矢量:

T3时刻定子电压矢量:

由式(2)和式(3)可以看出，在永磁同步电动机矢量控制系统中，由于参数的采集、矢量计算、控制信号的作用等过程导致控制滞后，实际输出的定子电压矢量与理想的定子电压矢量之间存在一定的误差，该误差:

由式(4)可以看出，实际输出的定子电压矢量比理想的定子电压矢量相位滞后ωeTD。由于PWM载波频率一定，随着电机转速的增加，相位滞后增大。当转速较高时，相位滞后尤为严重，如果不对控制量进行补偿，控制滞后会严重降低转速的控制精度，甚至会造成系统振荡。

为了消除控制滞后带来的消极影响，本文提出一种相位超前方式的补偿方法，对T0时刻的定子电压矢量us进行相位补偿，从而达到近乎零滞后的控制效果。补偿方法如下:

式中:θcomp为补偿相角。

式中:u*s为补偿后的定子电压矢量。

控制滞后的误差补偿控制系统结构框图如图4所示。

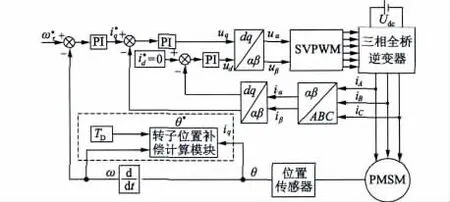
图4 控制滞后的误差补偿控制系统结构框图

2 仿真分析

在MATLAB /Simulink 中构建仿真模型如图5所示，控制系统采用磁场定向的速度、电流双闭环控制，控制策略则采用id= 0 的矢量控制策略。载波频率为10 kHz。仿真模型中，永磁同步电动机的参数如下:极对数2;额定功率15 kW;额定转速12 000 r/min;额定转矩15 N·m;额定电压270 V;额定电流63 A;定子绕组电阻0．054 5 Ω;d、q 轴电感0. 227 mH;转动惯量0．000 7 kg·m2;磁链ψ = 0．061 3 V·s。

图5 永磁同步电动机误差补偿控制模型

在经典矢量控制系统基础上，分别针对不存在控制滞后、存在控制滞后以及在存在控制滞后情况下采用补偿控制，进行仿真对比，以验证理论分析的正确性。其中速度环PI 参数:Kp_S= 15、Ki_S= 0．6;电流环PI参数为:Kp_C= 10、Ki_C= 0．5 ;负载为15 N·m。转速采用阶梯给定的方式，给定转速分别为1 000 r/min、3 000 r/min、6 000 r/min、9 000 r/min、12 000 r/min。

图6 为不存在控制滞后(理想情况下)的仿真结果，可以看到在理想情况下，反馈转速能精确地跟踪给定转速。

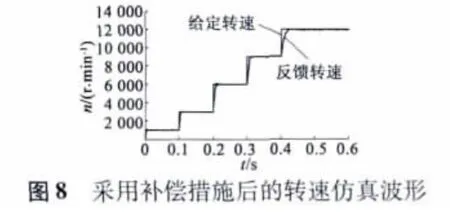
图7 为控制系统存在控制滞后的转速仿真波形，图中曲线是控制滞后时间分别为0．1 ms、0．07 ms、0．04 ms、0．03 ms 的仿真结果。可以看到，当电机运转于低、中速区间时，反馈转速能跟踪上给定转速，但存在较大的静态误差，并且该静态误差随着控制滞后时间的增加而增大。当电机运转于高速区间时，由于控制滞后的影响，反馈转速跟不上给定转速，并且控制滞后时间越长，电机转速所能达到的最高转速越低，而且转速波动越大，甚至出现轻微振荡。图8 为加入补偿控制后的仿真结果，可以看到，控制效果得到明显改善，反馈转速能很好地跟踪给定转速，转速误差约为± 1%。

3 实验验证

本文通过对一台15 kW、2 对极、额定转速为12 000 r/min 的永磁同步电动机搭建了矢量控制系统实验平台，进行误差补偿控制策略的验证。以TI公司的DSP－TMS320F2812 为控制核心，配合可编程逻辑器(CPLD)－EPM1270 来实现矢量控制算法;电流传感器采用串行AD 转换芯片AD7357，A、B相电流经信号调理电路后进行AD 转换，然后数据送至CPLD，再由CPLD 传送至F2812;转子位置检测采用高精度旋转变压器配合解码芯片AD2S1210，实时获取转子位置信息。本文在母线电压为270 V，给定转速为1 000～12 000 r/min 的条件下，对无补偿和有补偿的情况分别进行实验。图9、图10 分别为无补偿的转速实测曲线和电流实测曲线。图11、图12 分别为采用本文提出的补偿方法后的转速实测曲线和电流实测曲线。

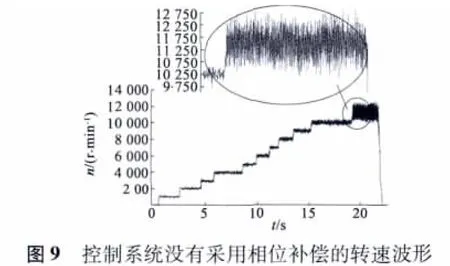
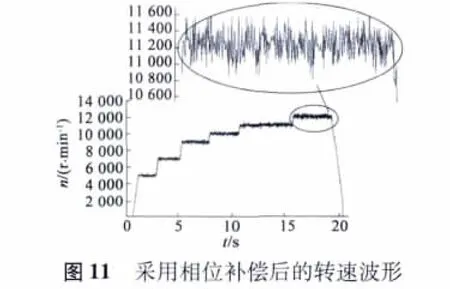
实验结果表明，不加补偿时，反馈转速能上升到11 000 r/min，但是波动极为剧烈，并出现轻微振荡。加补偿后，反馈转速能很好地跟踪给定转速，当给定转速为12 000 r/min 时，转速跟踪误差为2．5% 左右。由于仿真控制系统与实际控制系统存在着差异，导致实验结果与仿真结果不能完全一致，但总体基本相吻合。实验结果表明，本文提出的相位超前补偿方法可有效消除控制滞后所带来的消极影响，较大地改善了永磁同步电动机的控制性能。

4 结 语

针对永磁同步电动机矢量控制系统中存在的控制滞后问题，本文通过对控制过程中控制滞后现象的分析和所带来的矢量滞后相角的推导，提出了一种新型补偿控制算法。仿真及实验结果均表明了本文提出的补偿控制算法有效地改善了高速永磁同步电动机控制系统的稳态性能，为后续永磁同步电动机更高性能控制打下了良好的基础。

［1］ 何苗，刘政华．基于DSP 的无传感器永磁同步电机控制器设计［J］．微特电机，2010(10):63－65．

［2］ 杨南方，骆光照，刘卫国．误差补偿的永磁同步电机电流环解耦控制［J］．电机与控制学报，2011，15(10):50－54．

［3］ 张细政，王耀南，杨民生．永磁同步电机无位置传感器双滑模鲁棒控制［J］．电机与控制学报，2005，20(2):359－366．

［4］ 刘治钢，王军政，赵江波．永磁同步电机神经网络自适应滑模控制器设计［J］．电机与控制学报，2009，13(2):290－295．

［5］ Bae B H，Sul S K．A compensation method for time delay of full digital synchronous frame current regulator of PWM AC drives［J］．IEEE Transactions on industry applications，2003，39 (3):802 －810．

［6］ Choi C，Lee W．Analysis and compensation of time delay effects in hardware－in－the－loop simulation for automotive PMSM drive system ［J］．IEEE Transactions on industrial electronics，2012，59(9):3403－3410．