笼型转子磁力耦合器永磁体工作点校核

葛研军，温子淇，贾 峰，石运卓

(大连交通大学，辽宁大连116028)

0 引 言

磁力耦合器可通过气隙实现主动机到从动机之间的转矩传输，通过改变外转子(一般为永磁转子)和内转子(一般为铜盘或鼠笼转子)之间的气隙接触面积即可实现从动机输出扭矩和转速变化。具有空载起动、过载保护及高效节能等优点。

磁力耦合器主要分为盘式磁力耦合器和套筒式磁力耦合器。套筒式磁力耦合器按转子类型不同又分为实心转子磁力耦合器和笼型转子磁力耦合器。本文针对笼型转子磁力耦合器中永磁体的工况进行分析。

转矩是磁力耦合器传动机构中最重要的性能指标之一，准确计算磁力耦合器的传动力矩，是设计、分析磁力耦合器的关键［1］，而转矩与磁力耦合器的磁路构成及永磁体的工作点直接相关。磁力耦合器运行时，电枢反应及温度变化将使永磁体的工作点发生变化，为防止永磁体的工作点低于去磁点而造成不可逆去磁，必须保证永磁体负载工作点高于去磁点。

文献［2］采用标么值法进行磁路计算以获得永磁体的工作点，这种方法虽然计算简单，便于计算机求解，但不够直观，无法清晰地看出工作点与去磁点的关系。文献［3］采用“磁路”方法，给出了图解法求解永磁体工作点的模型，并对永磁体动态工况进行了深入分析，但并未对所求工作点进行校核。文献［4］采用磁路法获得永磁发电机外磁路中的磁通与磁势，并用图解法对永磁体工作点进行了校核。但其计算方法是以外电路中的电势为参照，而对笼型转子磁力耦合器而言不存在外电路，因而不适于校核笼型转子磁力耦合器中永磁体的工作点。

另外，为获取永磁体空载及负载工作点，首先应预估其空载时的工作点初值。与目前较为成熟的盘式磁力耦合器、实心转子磁力耦合器及永磁电机相比，笼型转子磁力耦合器空载工作点的初估值尚未有较为明确的取值范围。

针对上述问题，本文将磁路法与图解法相结合，对笼型转子磁力耦合器中永磁体工作点进行校核。首先基于外磁路磁导对永磁体工作点进行初估，然后利用磁路法计算出永磁体外磁路磁势及磁通，并利用磁势及磁通之间的关系得出笼型转子磁力耦合器外特性曲线。最后运用图解法求出永磁体在空载及负载工况下的工作点，并以此观察负载永磁体工作点与去磁点之间的关系。

上述方法既解决了磁路法不够直观的问题，也保证了工作点计算的准确性。因此将磁路法与图解法相结合既可简化计算过程又可清晰反映出空载及负载工况，适于计算机编程，有利于缩短计算周期，并便于进行参数化设计。

1 永磁体工况分析

永磁体工况的确定与其自身材料以及外界磁路组成密切相关，表现在工作图中为去磁曲线与外磁路特性曲线的交点。因此分析永磁体工况时首先应明确其外磁路组成。

图1 为笼型转子磁力耦合器示意图，其外磁路由永磁转子齿、永磁转子轭、空气隙、鼠笼转子轭及鼠笼转子齿组成。永磁体提供的磁通大部分匝链鼠笼笼条，少量散布在空气中。磁力耦合器空载时，永磁体工作点为去磁曲线与空载磁路外特性曲线的交点。负载时还须考虑电枢反应对工作点的影响。

图1 笼型转子磁力耦合器

2 校核方法

磁力耦合器中的永磁体尺寸确定后，应初估其空载工作点，主要用以校核磁力耦合器设计的合理性。

本文将磁路法与图解法相结合，首先估算出永磁体空载工作点Bm0，然后计算出每极气隙磁通Фδ0及空载特性，最后绘制出永磁体工作图并从中获得永磁体空载点B′mo。根据B′mo与Bm0所限定的允许误差，最终确定合理工作点。

图2 为永磁体工作点校核流程图。

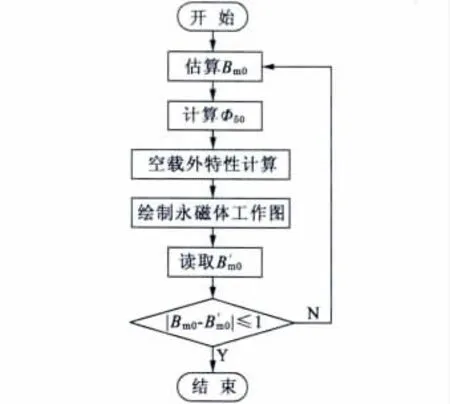
图2 校核流程图

3 磁路计算

笼型转子磁力耦合器的励磁磁场由外转子中的永磁体产生，永磁体既是磁源又是磁路的组成部分，其向外磁路提供的总磁通分为两部分:一部分与鼠笼笼条匝链，是实现机电能量转化的基础，称为主磁通;另一部分未与鼠笼笼条匝链，在永磁磁极之间及永磁磁极与构件之间形成磁场，称为漏磁通。

图3 为笼型转子磁力耦合器空载时外磁路的等效磁路。Фm为永磁体向外磁路提供的磁通;Fm为永磁体向外磁路提供的磁势;Λσ为主磁导;Λz1为永磁转子齿部磁导;Λδ为气隙磁导;Λz2为鼠笼转子齿部磁导;Λj2为鼠笼转子轭部磁导。

图3 外磁路等效磁路

3.1 初估永磁体空载工作点

笼型转子磁力耦合器设计完成后，须对其初估空载工作点进行校验。

图4 为空载时永磁体工作图。

设图4 中Q 点为空载工作点，其所对应的磁通及磁势分别为Фm0及Fm0。

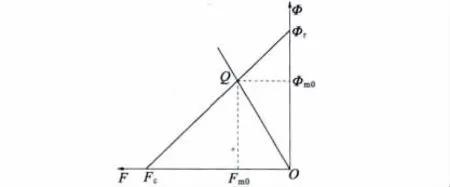
图4 空载时永磁体工作图

由图4 知:

式中:Фr为永磁体虚拟内禀磁通;Fc为永磁体磁动势源的计算磁动势。

永磁体工作点对应的磁通及磁势即为其向外磁路中提供的磁通及磁势。由外磁路中磁通、磁势及磁导的关系可知:

式中:Λδ为外磁路主磁导可由文献［5］获得;σ0为空载漏磁系数。

结合式(1)及式(2)得:

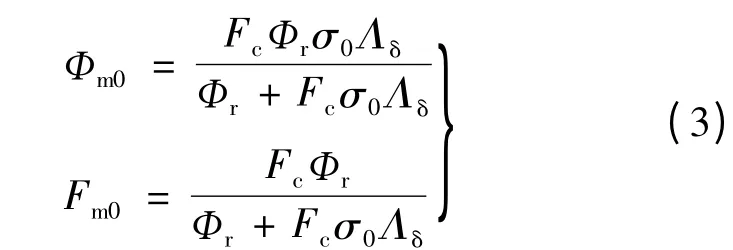
由电磁学公式Ф = BS，F = HL 可得出空载时永磁体工作点的表达式:

式中:Am为永磁体提供每极磁通的面积;Lm为永磁体充磁方向长度。

3.2 空载外特性计算

通过空载外特性计算可以获得永磁体向外磁路提供的磁通及磁势。根据磁路全电流定律，磁路中磁感应平均强度H 与磁路平均长度L 的乘积在数值上等于磁场的磁动势，则:

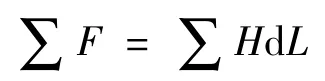
由于主磁路所包含的各部分磁场强度、截面积及材料不同。在计算外磁路总磁势时须分段对各部分磁势进行计算后再求和。

图5 为笼型转子磁力耦合器磁路示意图。其中Lz1为永磁转子齿部磁路平均长度;bp为永磁转子极弧长;Lj2为鼠笼转子轭部磁路平均长度;Lz2为鼠笼转子齿部磁路平均长度;δ 为气隙宽度;hz2为鼠笼转子齿宽;hj2为鼠笼转子轭部高度;tz为鼠笼转子齿距。

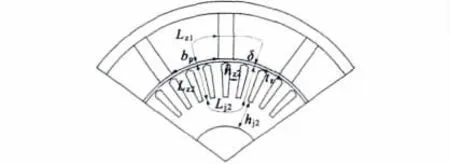
图5 磁路示意图

在各段磁路中，气隙的长度虽然最小，但由于空气的磁阻远远大于导磁材料的磁阻，所以在整个外磁路中，气隙磁势所占的比重最大［6］。为此首先讨论气隙磁势的计算。

设永磁体每极气隙磁通为Фδ0，气隙磁势为Fδ，则:

式中:μ0为真空磁导率;Bδ为气隙磁密;Hδ为气隙磁场强度;τ 为极距;l 为永磁体长度。

当磁通流经永磁转子齿部时，由于导磁材料的磁阻比空气磁阻小得多，因而可认为每极气隙磁通均由永磁转子齿中经过。设永磁转子齿部磁感应强度为Bz1，则:

鼠笼转子轭部流过的磁通为每极气隙磁通的一半，设鼠笼转子轭部磁感应强度为Bj2，则:

当磁通由气隙流经鼠笼转子齿部时，由于导磁材料的磁阻比空气磁阻小得多，因而可以认为一个齿距范围内的磁通都从鼠笼转子齿中经过。设鼠笼转子齿中的磁感应强度为Bz2，则:

根据所得的Bz1、Bj2及Bz2，即可从相应的导磁材料中查取其所对应的磁场强度Hz1、Hj2及Hz2。

设永磁转子齿部磁势为Fz1，鼠笼转子轭部磁势为Fj2，鼠笼转子齿部磁势为Fz2，则:

外磁路总磁势∑F:

4 图解法校核永磁体工作点

4.1 绘制永磁体工作图

永磁体去磁曲线描绘的是磁感应强度B 与磁场强度H 的关系，由于Ф = BS，F = Hb，通过变换比例就可将永磁体工作图中B－H 曲线坐标变换为Ф－F 坐标。同时，本文以虚拟内禀磁通Фr与磁动势源的计算磁动势作为磁通和磁势的基准值，使磁通与磁势在标么值中得到统一，以避免比例变换带来的不便。

永磁体工作点的确定与永磁体自身特性及外磁路特性有关。自身特性为永磁体去磁曲线。空载时的外特性可由空载特性计算获得的每极气隙磁通Фδ0与外磁路总磁势∑F 的关系描绘。

负载时，电枢反应磁场将对永磁体磁场产生去磁作用。磁力耦合器外磁路特性也将随之发生变化。电枢反应的去磁磁势Fad可以直接加到空载运行特性上，将空载特性曲线向右平移后即可获得负载外特性曲线，负载外特性曲线与去磁曲线的交点即为永磁体负载工作点。

表1 为一5．5 kw 笼型转子磁力耦合器结构参数，其中永磁体尺寸可由文献［7］、［8］获得。

表1 笼型转子磁力耦合器结构参数

表2 为该笼型转子磁力耦合器空载特性计算结果。

表2 空载特性计算结果

图6 为该耦合器中由永磁体自身特性及外磁路特性计算结果绘制的永磁体工作图。

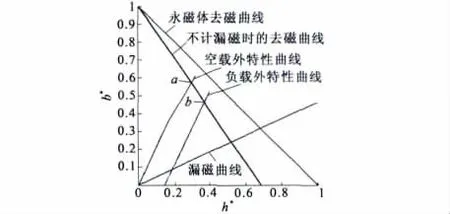
图6 永磁体工作图

4.2 工作点校核

磁力耦合器实际运行时，采用标么值绘制永磁体工作图，可以直接从图6 中读取永磁体工作点所对应的磁感应强度及磁场强度标么值。图6 中，a点纵坐标为空载工作点对应的磁感应强度标么值b′m0，a 点横坐标为空载工作点对应的磁场强度标么值h′m0。b 点纵坐标为负载工作点对应的磁感应强度标么值b′mN，b 点横坐标为负载工作点对应的磁场强度标么值h′mN。

因此，空载时永磁体工作点实在值:

式中:Br为剩余磁感应强度;Hc为矫顽力。本例磁体材料选用钕铁硼N35H，Br= 1．18T，Hc= 875kA/m。

计算图6 中所获得的工作点值与工作点初估值之间的误差，并设定两者之间的误差值为1%。若小于1%，则该初估值在合理范围内。若二者差值大于1%，则调整漏磁系数重新对工作点进行初估，直到二者误差小于1%。

本例中，初估工作点空载磁感应强度实在值和空载磁场强度实在值分别为Bm0= 0．860 T 和Hm0=238．5 kA/m。由工作图中获得的空载磁感应强度标么值为b′m0= 0．724，即空载磁感应强度实在值为B′m0= 0．854 T。由工作图中获得的空载磁场强度标么值为h′m0= 0．271，即空载磁场强度实在值为H′m0= 237 kA/m。初估值与由工作图获得值间误差:

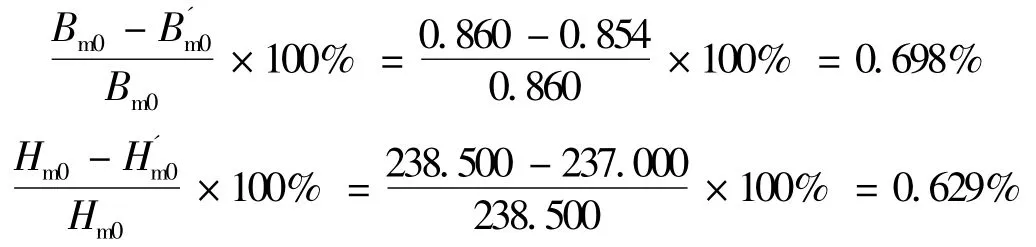
同时，负载工作点高于图6 中的去磁点K，电枢反应的影响不会导致永磁体完全去磁。

5 结 论

(1)磁力耦合器中永磁体工作点与其外磁路构成及电枢反应直接相关;运行工况不同，其永磁体工作点也就不同。

(2)采用磁路法求解，并用图解法进行补充分析，既可以检验磁力耦合器磁路是否饱和，也可以直接从永磁体工作图中观察出永磁体工作点与去磁点的关系。

(3)根据式(4)、式(10)及式(11)，利用计算机编程来实现磁路计算和工作图绘制，即节省时间又可确保计算的准确性，便于磁力耦合器的参数化及系列化设计。

(4)图解法可用以校核永磁体工作点。同时通过观察永磁体工作图中的负载工作点，可以判断永磁体是否会出现完全去磁的情况。

［1］ 葛研军，聂重阳，辛强．调制式永磁齿轮气隙磁场及转矩分析计算［J］．机械工程学报，2012，48(11):157－162．

［2］ Lan Z Y，Yang X Y，Zheng C D，et al．Analysis of an improved magnetic circuit for designing interior permanent magnet synchronous motor［J］．IEEE Conference Publications，2010:3320 －3323．

［3］ 佟为明，李凤阁，赵志衡．单永磁极化磁系统的永磁工作点图解法统一模型与分析［J］．中国电机工程学报，2005，25(6):129－133．

［4］ 李钟民，刘卫国．稀土永磁电机［M］．北京:国防工业出版社，1999:27－33．

［5］ 曹卫东，施卫东．退磁曲线法和磁导法的磁力泵耦合器转矩分析［J］．农业机械学报，2004，35(2):145－149．

［6］ Ge Y J，Nie C Y，Xin Q．A three dimensional analytical of the air－gap magnetic field and torque of coaxial magnetic gears ［J］．Progress In Electromagnetic Research，2012，131:391－407．

［7］ Zhang B Y，Zhang W，Zhuang F Y，et al．Design and starting process analysis of multipolar line－start PMSM［J］．IEEE Conference Publications，2007:8－11．

［8］ Feng Y J，Cai W L，Yang K，et al．Design and optimization of servo permanent magnetic synchronous motor［J］．IEEE Conference Publications，2008:3307－3310．