基于刚柔耦合模型的火箭炮发射动态响应研究

崔龙飞，张 龙，罗 云，陈福红，马 威

(1.南京理工大学 机械工程学院，江苏 南京 210094；2.中航工业洪都660研究所，江西 南昌 330024)

火箭炮发射是一个高瞬态、强冲击、非线性的复杂过程，各部件之间存在剧烈的接触碰撞。用多刚体动力学方法进行仿真计算时，由于忽略了各构件的弹性变形，结果存在局限性和不准确性。为考虑定向管、俯仰轴、发射装置底座的变形对动力学响应过程的影响，利用有限元分析软件ABAQUS建立柔性部件有限元模型，通过外部节点设置和模态计算，获得模态中性文件，利用ADAMS-Flex柔性模块导入仿真模型，建立可以处理刚柔接触问题的刚柔耦合发射动力学模型，并通过动力学计算得到发射装置的动态响应特性。为火箭炮结构优化设计和减小初始扰动做准备，具有一定的理论意义和实用价值。

1 刚柔耦合多体动力学方程的建立

火箭炮刚柔耦合系统中，刚体按照多刚体动力学理论建立方程，而柔性体用有限元法建立方程，将两者组集就可以得到刚柔耦合的多体系统动力学方程[1]。

ADAMS采用的是欧拉-拉格朗日建模方法，选取系统内每个零件的质心在惯性参考系的3个直角坐标和3个欧拉角为笛卡尔广义坐标，求解思路：对火箭炮系统中的各个构件建立坐标系，进而获得整个多体系统中任意点的位置、速度和加速度，从而推导出系统中各个构件的动能、势能及广义力等参数，最终建立构件的动力学方程，最后将约束吸收到动力学方程中，形成整个多体系统的刚柔耦合模型。其中，拉格朗日乘子法建立第i个柔体的动力学方程为：

Φ为约束方程；柔体坐标系的位置用其在惯性参考系中的笛卡儿坐标r=(x,y,z)、反映刚体方位的欧拉角ψ=(ψ,θ,φ)以及模态坐标q=(q1,q2,…,qN)(N为模态坐标数)来表示，综合考虑柔性体变形前后的位置、方向和模态，柔性体的广义坐标表示为：

ξ=[x,y,z,ψ,θ,φ,qi]T=[rψq]T

其中，i=1,…,N；λ为对应于约束方程的拉氏乘子；Q为投影到ξ上的广义力；L为拉格朗日项，定义为L=T-W，T和W分别表示动能和势能；Γ表示能量损耗函数。将求得的T,W,Γ代入上式，得到最终的运动微分方程为：

2 刚柔耦合模型的建立

2.1 模型总体结构及运动副定义

多管火箭炮发射系统是复杂的机械系统，在建模过程中，根据其结构特点，可将全炮分为：底座、回转机构(电机、减速器等)、俯仰机构(电机、减速器及主轴)、发射箱(定向管、火箭弹)四大部分。根据发射系统实际结构和运动情况，建立其拓扑结构如图1所示，发射过程中弹性变形较大的几个部件(定向管、俯仰轴、底座)在仿真中定义为柔性体，火箭炮刚柔耦合模型如图2所示。

2.1.1 回转、俯仰运动副的定义

回转体绕底座中心轴做方位回转运动，实现方位瞄准，在回转体与底座之间通过回转盘连接，在连接位置建立转动副，为了模拟发射时冲击力矩引起回转体与底座间的弹性变形，在转动副处添加扭簧阻尼器，刚度和阻尼系数由试验测得。发射箱绕俯仰轴中心线做俯仰运动，实现高低方向瞄准，左右发射箱分别与俯仰轴上的法兰盘固连，在俯仰轴与回转体之间定义转动副，同时在俯仰旋转副处添加扭簧阻尼器来模拟发射箱与回转体间的弹性变形[3]。

2.1.2 火箭弹与柔性定向管间的接触碰撞

火箭弹在螺旋定向管内的运动实际上是一个复杂的过程，火箭弹在沿定向管运动过程中伴随着定心部与定向管内壁的剧烈碰撞，同时定向钮在螺旋导槽内受迫运动，带动火箭弹转动，达到一个合理的出口转速。通过定义3个定心部与定向管之间的碰撞接触约束以及定向钮与螺旋槽的碰撞接触约束，模拟火箭弹在定向管中螺旋式前进的过程。

2.2 柔性体建模

火箭弹发射过程中，定向管受到定心部的撞击力、定向钮对螺旋导槽的碰撞力，俯仰轴承载着左右发射箱的重力，底座承载着整个发射装置的重力，而且还受到发射冲击载荷的作用，存在较明显的弹性变形，对系统的动力学响应和火箭弹的运动特性有较大的影响，看作刚体模型计算，结果将存在较大误差，为提高仿真分析精度，进行柔性化处理。

利用有限元软件ABAQUS对这些部件进行离散处理，先定义材料参数，定向管材料为玻璃钢，轴和底座为45钢。然后对这些部件进行单元设置和网格划分，采用六面体单元C3D8R，并在与其它部件的连接点处建立的界面点，使用模态综合法计算结构的约束模态和固定界面模态，得到用于描述柔性体变形所需的模态集。通过软件接口程序生成创建柔性体模型所需的模态文件[4]。通过ADAMS中Flex接口导入模态文件，得到相应结构的柔性体模型，设置合适的响应频率或模态，并利用界面点施加作用在柔性体上的约束和载荷，完成刚柔耦合模型的建立[5]。

2.3 发射系统激励力的加载

2.3.1 闭锁力

为了保证火箭炮在发射前或运输途中火箭弹可靠的固定于定向管内，点火装置能够可靠接通，需要在定向管上安装闭锁挡弹装置。闭锁挡弹装置对弹提供闭锁力，发射时火箭弹必须克服闭锁力使闭锁装置解锁才能运动，该发射装置的闭锁力大小约为弹重的1.5倍，为了在动力学模型中体现闭锁力的影响，在定向管与火箭弹之间定义轴套力约束，发射时当火箭弹的推力达到闭锁力后，利用脚本语句使轴套力约束失效。

2.3.2 火箭弹发动机推力

发动机点火后，推力使火箭弹挣脱闭锁挡弹装置的约束，沿定向管向前运动。火箭弹发动机推力数据由试验测得，按照Akima二次曲线拟合方法得到样条曲线函数(以时间为自变量，力大小为变量)，将推力用IF函数形式描述为：IF(time-launch：0，0，AKISPL(time-launch，0，Spline_1，0))，并通过集中力作用于火箭弹尾部，式中time表示仿真分析的当前时刻；launch表示第n发火箭弹发动机点火时刻；Spline_1表示调用的火箭弹推力样条曲线名称，如图3所示。

2.3.3 火箭弹燃气射流冲击力

对于多管火箭发射装置，火箭弹的燃气流冲击力是火箭发射装置产生振动的重要因素，进而对由发射装置振动引起的初始扰动产生重要影响。火箭弹的燃气流场由Fluent软件计算得出，计算流场坐标系x轴垂直于迎气面向内，z轴垂直于束向瞄准平面向上，图4为火箭弹燃气射流冲击力沿坐标轴分量随距离(弹尾与管口的距离)变化曲线。

将三个方向分力分别施加到定向管纵向轴线与炮口平面交点，火箭弹脱离管口后，射流核心区域作用于管口时，燃气射流冲击达到最大，随着火箭弹的远离而迅速减小，冲击力随距离变化的规律用Akima二次曲线拟合插值得到，冲击力函数表达式为：IF(length-5000:AKISPL(length，0，Spline_i，0)，0，0)，length表示火箭弹尾部距离定向管口的距离，Spline_i(i=x,y,z)是燃气射流冲击力沿坐标轴分量的样条曲线名称[6]。

3 模型仿真分析

对某一典型发射方式(两枚齐射)进行刚柔耦合发射动力学仿真，一组两发弹，按照“先左后右，先上后下”的顺序，分四组完成一轮射击，射击时间间隔175 ms，总仿真时间705 ms,俯仰角为42°，方位角为0°。

3.1 弹-管碰撞分析

对火箭炮发射进行仿真计算，得到火箭炮各部件的动态响应数值结果，火箭弹3个定心部和定向钮与定向管的碰撞作用力曲线如图5～图8所示。

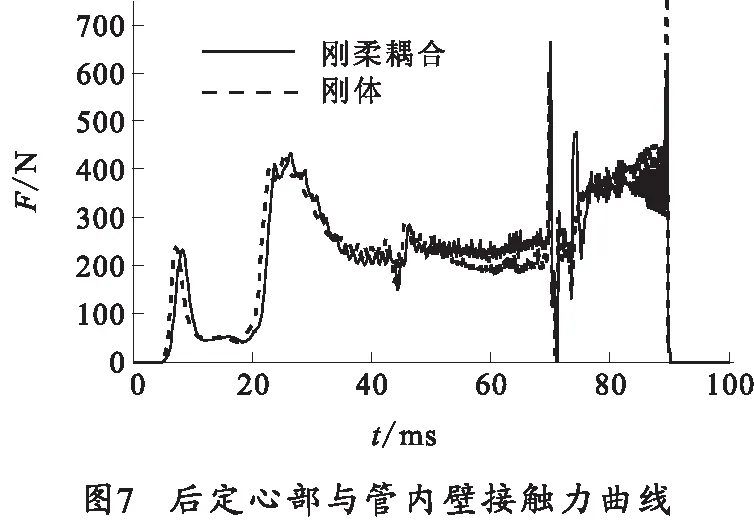
观察图5～图8接触力-时间曲线，对比刚柔耦合模型与多刚体模型的仿真结果，可以看出：

1)在火箭弹点火到尾部离管的91 ms内，由于定向管柔性弹性变形、阻尼的作用，火箭弹在柔性管内运动产生的管口振动连续蠕动变化、相对平缓，接触力的第一个峰值出现较晚，多刚体模型的第一个曲线峰值出现较早。

2)刚柔耦合模型中接触力曲线存在大量连续不断的微小颤动，与实际情况相吻合，较准确地模拟了火箭弹在管内复杂的接触碰撞过程。

3)多刚体模型中，定心部、定向钮脱离定向管管口时接触力都存在较大的峰值，而刚柔耦合模型中相对较小，这是由于柔性体阻尼的存在使得运动过程接触力变化较小。

3.2 定向管初始扰动分析

为了清晰的反应出闭锁力、弹管碰撞等引起的定向管的扰动，取第一组火箭弹发射过程的仿真结果进行分析，测量定向管管口中心点在高低瞄准平面和束向瞄准平面内的线速度和角速度，如图9和图10，由于柔性体阻尼的存在，定向器管口测量点角速度、线速度衰减较快；而由于定向管、俯仰轴、底座的弹性变形的影响，定向器管口线速度与角速度并不是简单的线性关系，刚柔耦合模型中定向管管口振动曲线变化规律更复杂，结果更符合实际情况。

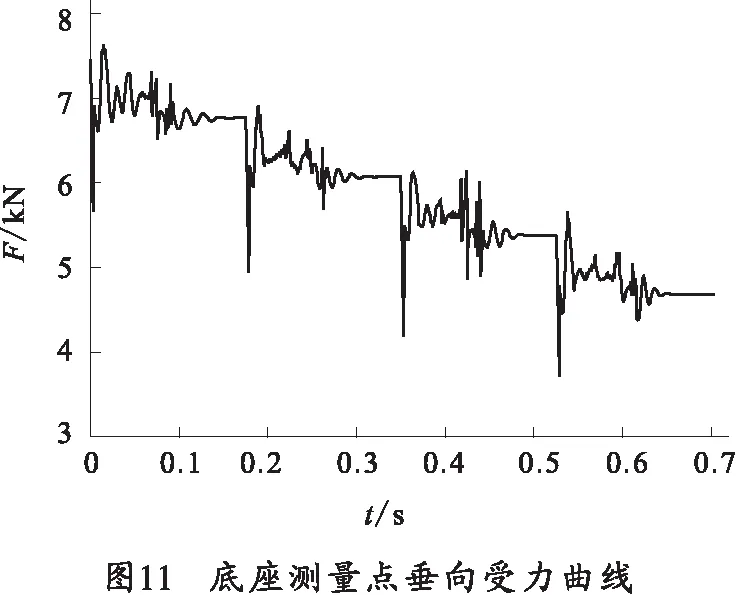
3.3 底座受力与响应分析

四组火箭弹依次发射，完成一轮射击，历时705 ms，测量柔性底座与回转盘固定副处界面点的垂直方向的受力如图11，该点垂直方向位移历程曲线如图12所示。由仿真结果可知：垂直方向受力较大，主要受到发射装置重力和激励载荷的作用，在火箭弹脱离管口之前，由于存在复杂的接触碰撞作用力-时间曲线都存在较大峰值的波动，火箭弹出口后，衰减较快。

从图12中可以看出，火箭弹在定向管内滑行阶段，底座竖直方向位移波动比较大，最大峰值78 μm，引起的扰动比较明显，底座的变形在动力学研究中是不能忽视的。

4 结束语

运用动力学仿真分析软件ADAMS，建立了某型火箭炮发射装置的刚柔耦合模型，考虑定向管、俯仰轴、底座弹性形变对动态特性的影响，将其定义为柔性体，对模型动力响应过程进行仿真分析，深入研究了发射过程中火箭弹定心部、定向钮与柔性定向管之间的碰撞、定向管的振动以及底座的弹性变形和受力。结果表明，柔性部件的变形影响火箭弹出管口的初始扰动，进而会影响射击精度，该研究对于减小火箭弹的初始扰动和提高射击精度具有参考价值。

[1] 韩清凯，罗忠.机械系统多体动力学分析、控制与仿真[M].北京：科学出版社，2010：97-103.

HAN Qing-kai，LUO Zhong. Control, simulation and dynamics analysis of multi-body mechanical systems[M].Beijing：Science Press，2010：97-103. (in Chinese)

[2] 陈立平，张云清，任卫群，等.机械系统动力学分析及ADAMS应用教程[M].北京：清华大学出版社，2005：56-57.

CHEN Li-ping，ZHANG Yun-qing，REN Wei-qun，et al. Dynamic analysis of mechanical system and ADAMS application tutorial[M].Beijing：Tsinghua University Press，2005：56-57. (in Chinese)

[3] 李军，马大为，曹听荣，等.火箭发射系统设计[M].北京：国防工业出版社，2008：213-215.

LI Jun，MA Da-wei，CAO Ting-rong，et al. Design of the rocket launcher system[M].Beijing：National Defense Industry Press，2008：213-215. (in Chinese)

[4] 陈余军，姜毅.车载导弹行进间发射动力学仿真分析[J].弹箭与制导学报，2011，31(1)：55-57.

CHEN Yu-jun，JIANG Yi. Dynamic simulation analysis of mobile missile launching on the move[J].Journal of Projectiles，Rockets，Missiles and Guidance，2011，31(1)：55-57. (in Chinese)

[5] 傅德彬，姜毅.基于刚柔耦合模型的发射装置动力学仿真分析[J].系统仿真学报，2009，21(6)：1789-1793.

FU De-bin， JIANG Yi. Dynamics simulation of guided missile launcher based on coupled rigid and flexible model[J]. Journal of System Simulation，2009，21(6)：1789-1793. (in Chinese)

[6] 王雷，马大为，周克栋，等.防空火箭炮刚柔耦合发射动力学仿真[J].弹道学报，2012，24(4)：72-76.

WANG Lei，MA Da-wei，ZHOU Ke-dong，et al. Simulations of rigid-flexible coupling launch dynamics for antiaircraft rocket launcher[J].Journal of Ballistics，2012，24(4)：72-76. (in Chinese)