理想状态下弹丸身管耦合系统动力响应特性研究

吴会民，宋春霞，王宝元，邵 婷

(1.西北机电工程研究所，陕西 咸阳 712099；2.海军蚌埠士官学校，安徽 蚌埠 233012)

弹丸膛内运动、炮口起始扰动对弹丸的射击精度有着密切的关系，因此，研究膛内时期弹丸运动规律，以获得弹丸出炮口瞬时的运动姿态显得十分重要。

传统的膛内时期弹丸运动规律研究是将弹丸视为质点，不能很好的反映弹丸身管的耦合关系和弹丸出炮口的姿态。随着计算机技术的发展和数值计算理论与方法的成熟，对弹丸膛内运动规律的研究逐渐深入，文献[1]将膛内运动的弹丸由质点模型假定为刚体模型，并假定弹带中心沿炮膛轴线运动，研究了弹丸在柔性身管中的运动；文献[2]仍然以刚体动力学理论为基础上，建立了较为完善的弹丸膛内外发射动力学模型，运用凯恩方法推导了弹丸膛内运动过程的动力学方程，编制了相应的软件；文献[3]采用有限元法研究了M829高速动能弹炮口初始扰动与射击精度的关系；文献[4]采用DYNA3D软件，建立了37mm火炮陶瓷喷嘴瞬态热固耦合动力学有限元模型。但是，目前的模型很少涉及到对弹带与膛线的描述，主要原因是软质材料弹带和身管膛线相互作用过程中会发生塑性变形，多刚体动力学无法描述这一现象。

笔者主要考虑弹丸重力、弹丸质量偏心、起始装填角等对弹丸身管耦合系统动力响应影响因素，并本着由简至繁的原则，不考虑身管弯曲、弹底压力推力偏心等因素，将弹丸身管耦合假设为理想状态，建立弹丸身管耦合系统有限元模型[5]，并利用波动理论[6]研究理想状态下弹丸身管耦合系统动力响应。

1 计算模型

1.1 有限元模型

首先利用UG建立了某型火炮身管和弹丸耦合系统实体模型。利用前处理软件ANSA对实体模型进行有限元建模。有限元模型如图1所示。

1.2 材料模型

本研究中弹丸以及身管材料都采用普通炮钢，炮钢材料为35CrNiMoVA，身管和弹丸材料模型为各向同性线弹性材料模型。弹带材料为工业纯铁，采用JohnsonCook屈服模型。

1.3 载荷及边界条件

身管根部为固定端约束，弹底施加膛压时间曲线，膛压时间曲线见文献[5]。

2 身管动力响应研究

2.1 身管动力响应分析方法

根据所建立的计算模型，利用弹性动力学理论[7]分析表明：弹丸膛内运动期间，身管有轴向振动、扭转振动、横向振动，且各个方向振动互相耦合。同时身管应变波有纵波、横波，这些弹性波沿着身管表面进行传播[6]。

为了研究身管的动力响应，取身管一横截面，考察截面上水平(x方向)和高低(y方向)上的位移，研究其动力响应特征。截面上每点位移信息由两部分组成，一方面是转动产生的位移，另一方面是平动位移。

为了研究身管横向振动和扭转振动，需要将各节点位移信息分离。注意到身管扭转时，扭转引起的身管上表面x方向和下表面x方向位移方向相反;身管动力响应位移量与身管直径相比为小量等规律，可以通过将上下表面节点位移曲线叠加消除扭转引起的影响。将得到的曲线幅值除以2就得到了横向振动引起的位移，从而也可以得到扭转振动引起的位移。

2.2 身管动力响应特征研究

采用上述方法将身管表面对称各节点位移曲线进行分离，分别得到了身管扭转振动和横向振动的位移变化，如图2所示。

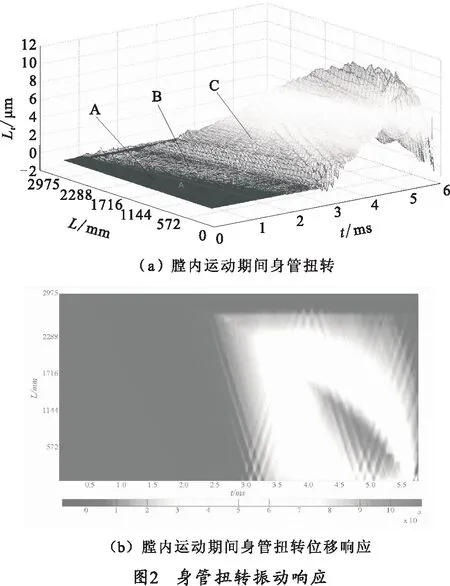
图2(a)表明，身管扭转位移随时间演化图可以分为3个部分，如图中A、B、C示。A区域表示弹丸从静止开始到完成挤进过程，该区域内基本没有扭转振动。挤进完成时刻至弹丸运动到等齐膛线与渐速膛线交点时，身管产生了小幅值的高频扭转响应，如图中B区域所示。

当弹丸完全嵌入膛线，开始运动时，膛线通过弹带将对弹丸产生一个扭矩脉冲，在扭矩脉冲作用下，弹丸产生扭转振动响应；同时弹带也将通过膛线产生反作用下，扭矩脉冲，在该扭矩脉冲作用下,身管产生高频低幅值扭转振动响应。扭矩脉冲的幅值与缠角和该时刻膛底压力有关。在膛压作用下，弹丸沿身管移动，随着沿身管纵向距离的增加，膛线缠角逐步增大，当弹丸运动到等齐膛线与渐速膛线交点时，身管产生显著扭转变形。随着弹丸在膛内纵向运动距离增加，该扭转角进一步增加，表现为扭转产生的位移增加，如图中C区域所示。B区域为扭转冲击下身管结构波动响应，C区域为扭转载荷作用下身管整体结构响应。

图2(b)用色标清晰展示了身管扭转振动中扭转波的传播与反射。弹丸运动2.0 ms时，扭转波动响应开始，弹带与身管相互作用产生扭转扰动，扭转扰动以波动形式沿身管传播。当扭转波传播到炮口时将进行反射，入射扭转波与反射扭转波具有相同的速度，扭转波不发生弥散。同时在弹丸运动迹线上每一时刻都会产生扭转脉冲，分别沿身管正向(炮口方向)和负向传播。当弹丸运动5.0 ms时刻距离炮口约800 mm处身管产生最大扭转位移。

图3给出了身管x方向响应位移时间演化图。演化图分为A、B、C三个区域，其中A区域表示从弹丸开始运动到弹丸挤进结束时刻身管动力响应；B区域表示从弹丸挤进结束到弹丸运动到等齐膛线与渐速膛线交点时身管动力响应；C区域表示从弹丸运动到等齐膛线与渐速膛线交点时开始到弹丸出炮口时刻身管动力响应。

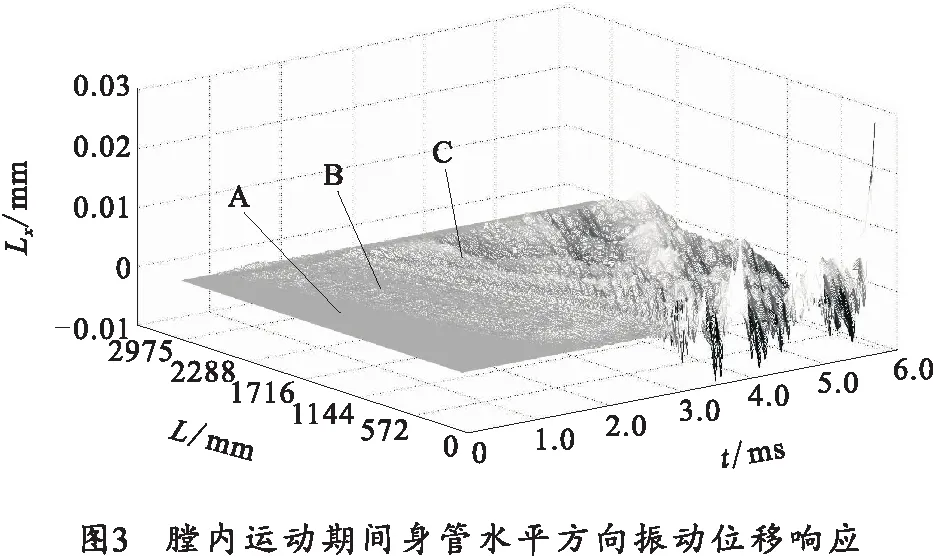
从图3中可以看出,膛内运动期间，身管x方向动力响应特征为弯曲波动响应。弹丸运动到等齐膛线与渐速膛线交点处，炮口x方向位移产生明显响应，这是由于当弹丸运动到等齐膛线与渐速膛线交点处时，身管产生明显扭转变形，与之耦合的横向振动幅值也逐渐增加。横向弯曲波沿身管传播到炮口处时，将进行卸载，引起炮口大幅值振动。

膛内运动期间，与扭转振动耦合的水平方向横向位移量级为1 μm，其最大位移在5.75 ms时在炮口位置处，其最大位移量级为10 μm。

通过以上分析，可以看出对炮口水平方向振动影响显著的时间段为弹丸运动到等齐膛线与渐速膛线交点处开始到弹丸出炮口时刻。弹丸挤进以及弹丸运动到等齐膛线与渐速膛线交点处时对x方向身管位移影响不明显。

图4为膛内运动期间身管高低方向振动位移响应。从图4中可以看出，身管高低方向动力响应特征与水平方向相同。

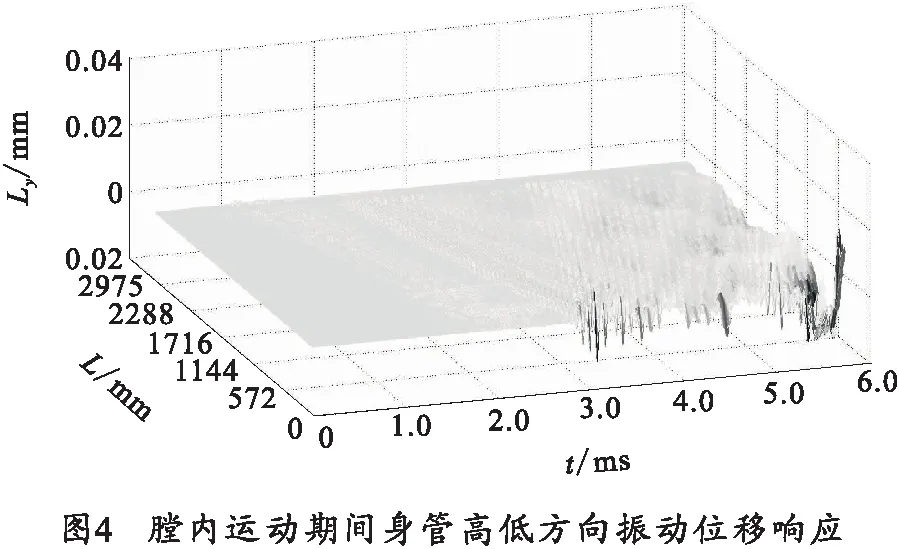
以上分析表明，弹丸身管耦合系统膛内时间(约束期和半约束期内)动力响应特征为波动响应，身管没有产生整体结构响应；最大位移在炮口处，幅值为微米量级。

3 弹丸动力响应研究

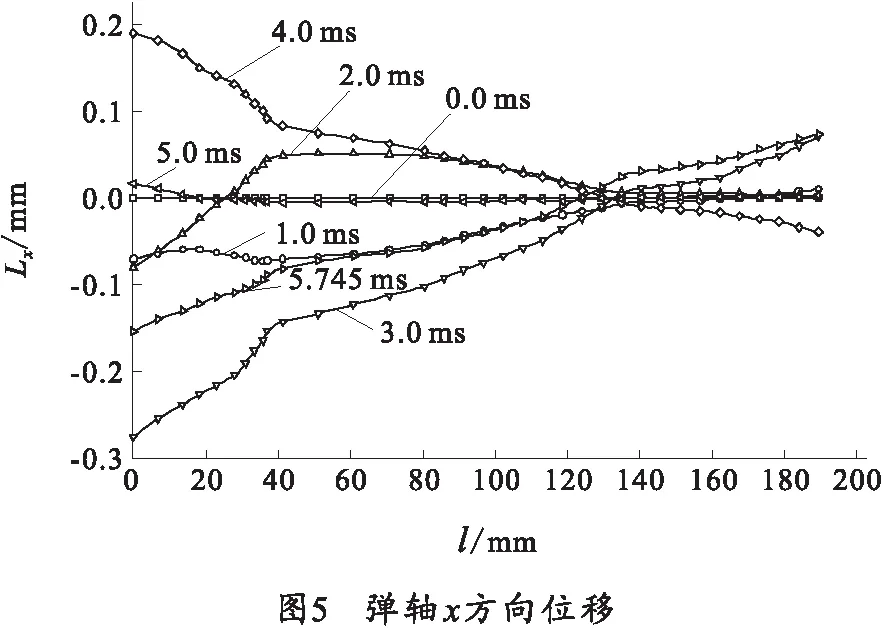
图5为弹轴不同时刻x方向位移变化。纵坐标为弹轴上各点在x方向位移，横坐标为弹轴长度方向坐标。从图中看出，0时刻弹轴上各点x方向位移均为零；随时间增加，绕0值上下波动，且幅值随时间增加呈现增加趋势。与刚体模型相比，弹性体模型更精确地反映了弹丸膛内运动的特征。膛内运动期间弹轴为曲线，且随时间章动。

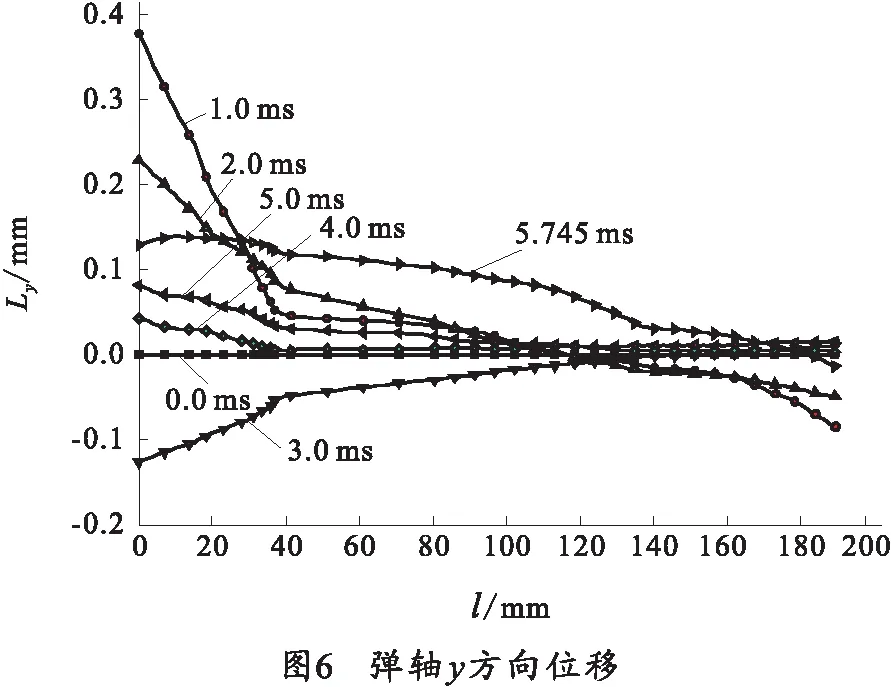
图6为弹轴不同时刻y(高低)方向位移变化。纵坐标为弹轴上各点在y方向位移，横坐标为弹轴长度方向坐标。

4 半约束期弹丸身管响应研究

4.1 半约束期身管动力响应分析

自弹丸前定心部离开炮口瞬间至弹带脱离炮口膛线这一段时间，称为半约束期。这个时期前定心部己经脱离了炮膛的束缚，弹带仍受膛线约束，弹速与转速仍在增加。炮口y方向位移时间曲线如图7所示。

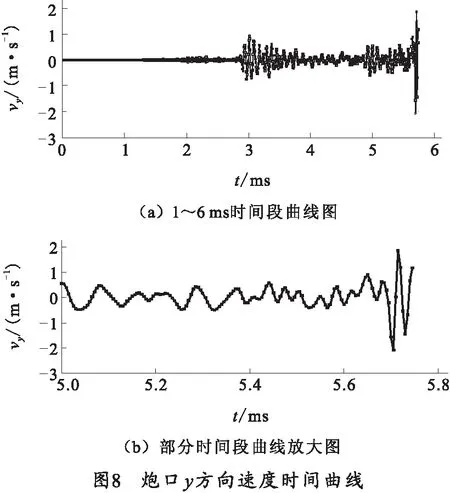
从图7中可以看出，半约束期内横向振动位移与约束期内相比，波动频率增加，同时波动幅值显著变化。这表明，半约束期内炮口横向速度和加速度将会产生改变。

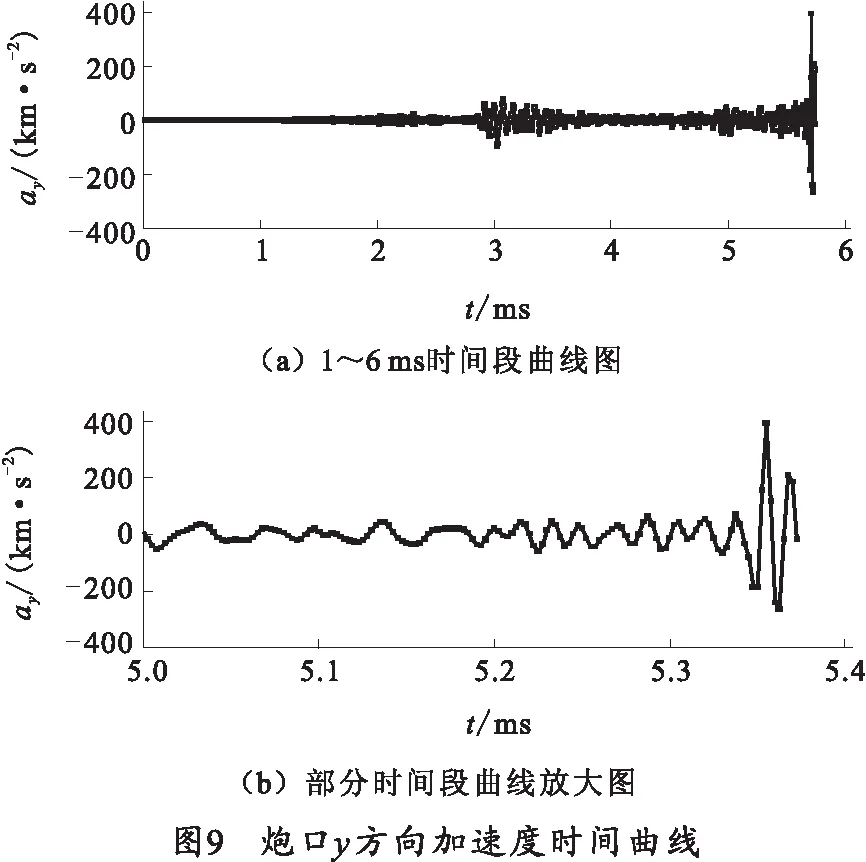
为了进一步分析半约束期内炮口横向速度和横向加速度的变化，图8和图9给出了炮口横向振动速度和加速度曲线以及部分时间段放大图。从图8和图9中可以看出，半约束期内炮口横向速度和加速度波形变化趋势是频率和幅值显著增加。

4.2 弹丸半约束期动力响应特征分析

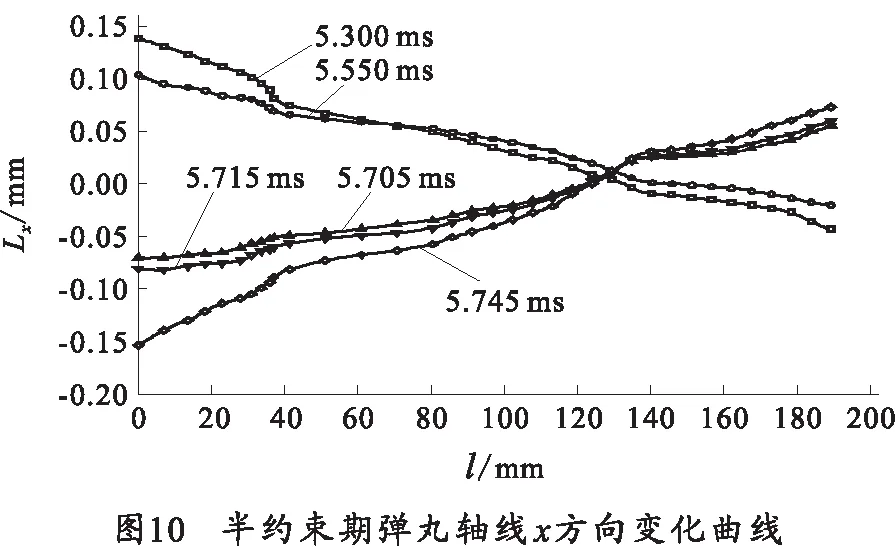
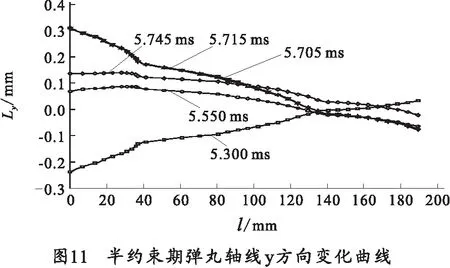
图10和图11分别给出了半约束期弹丸轴线x方向和y方向位移随时间变化结果。

可以看出，弹带脱离炮口过程中，在x方向和y方向弹丸轴线变化不明显；半约束期弹丸身管耦合使得脱离过程中炮口质点速度和加速度时间曲线波形产生显著变化，表现为幅值和频率的增加；由于半约束期弹丸运动时间为36μs，弹丸瞬态响应无法在结构动态响应上体现出来，所以半约束期弹丸轴线位移时间曲线无法给出半约束期影响，需要后续工作深入研究。

5 结束语

笔者采用数值计算方法对弹丸身管耦合系统的动力响应进行研究，得到了身管扭转振动和横向振动的基本规律。

结果表明，在理想状态下，身管扭转响应早期为波动传播，通过扭转波的传播与反射，逐渐过渡到结构整体扭转响应；身管横向动力响应基本为波动响应，没有形成完整的结构响应。当弹丸出炮口

时，最大波动幅值位于炮口处，约为微米量级。半约束期内，身管炮口横向动力响应产生显著变化，主要表现为波动频率和幅值增加。同时通过对弹丸身管耦合系统的动力响应数值研究，得到了弹丸运动的基本规律。采用弹丸轴线和轴线上特征点对弹丸运动进行了研究，得到了弹丸姿态角的变化规律。

[1] T S MARTING,S B ROBERT，Projectile motion in a flexible gun tube[R].AD-A140737, 1984.

[2] 吴宏.弹丸膛内外运动及其对射击精度影响研究[D].南京：南京理工大学，2001.

WU Hong. The study on projectile movement in &out gun tube and its effects to firing accuracy[D]. Nanjing: University of Science and Technology,2001. (in Chinese)

[3] ERIE KATHE，STEPHEN WILKERSON, ALEXANDER ZIELINSKI, et al. Gun structural dynamic considerations for near-target performance of hypervelocity launchers[R]. AD-A355932, 1998.

[4] CONROY PAUL,GARNER JAMES.A 37 mm ceramic gun nozzles stress analysis[R]. AD-A449926，2006.

[5] 吴会民.弹丸膛内运动分析[J].火炮发射与控制学报，2011(4)：62-65.

WU Hui-min. The analysis of the projectile moving characters in the barrel[J]. Journal of Gun Launch & Control,2011(4)：62-65. (in Chinese)

[6] F KARL. GRAFF. Wave motoion in elastic solid[M]. Oxford：Oxford University Press，1991.

[7] 王礼立.应力波基础[M].北京：国防工业出版社,2005.

WANG Li-li. Foundation of stress wave[M]. Beijing：National Defense Industry Press，2005. (in Chinese)