基于AHP群决策的火炮内弹道方案评价

王 敬,陈志武,何 云

(空军空降兵学院，广西 桂林 541003)

内弹道设计的任务是根据武器的战术技术要求和外弹道设计方案提供的口径、弹丸质量及炮口速度等初始数据，选定适当的炮膛结构参数，确定出符合武器性能要求的一组可行方案，即可行方案集，并对可行方案集进行评价。基于经典内弹道学的评价指标一般包括炮膛最大压力pm、炮口速度vg、炮口压力pg、有效功效率ηω及炮膛工作容积利用率ηg[1]。文献[2]将可行方案的评价过程作为一类(单人)多指标决策问题，提出了一种基于多指标的火炮内弹道设计方法，建立了某火炮的内弹道设计方案多指标优化模型，并采用TOPSIS法对可行方案集进行了评价排序；文献[3]、[4]分别应用熵权法和方案满意度法对某型火炮的可行方案集进行了评价排序。但是，当有多名决策者参与评价时，可行方案集的评价排序过程将成为一类多人多指标决策问题，即多指标群决策问题。与(单人)多指标决策不同的是，多指标群决策问题不仅要计算指标权重，还要确定各专家(决策者)的权重。一般的处理方法是，不考虑专家之间的差异，假定各专家对问题的影响力是均等的，或针对不同领域的决策者给定不同的权重。笔者以层次分析法(AHP)分析为基础，采用AHP对数最小二乘法计算指标权重，获得各专家的指标权重矩阵；专家权重由AHP判断矩阵的一致性和判断矩阵之间的相似程度来确定；指标的综合权重则由专家权重对指标权重进行聚合而得到，最后由指标的综合权重对可行方案集进行线性加权综合，获得可行方案集的优劣排序结果。该方法能充分客观地综合专家的群体智慧和经验，弱化单个专家主观上的不确定性，使弹道方案的评价结果更具客观性和权威性。

1 指标权重与专家权重

假定有m个专家(E(k),k=1,2,…,m)对具有n个指标的可行方案集进行评价，设专家Ek的判断矩阵为：

专家E(k)(k=1,2,…,m)的指标权重是该专家对各评价指标在评价过程中的重要性的数值表示，基于AHP的指标权重可由AHP的各种计算方法(如特征向量法、对数最小二乘法、最小二乘法、最小偏差法等)计算得到，记为ω(k)。指标权重ω(k)仅由判断矩阵A(k)决定，并没有考虑其一致性和与相似性的影响，而专家在群决策过程中的作用，即影响力，则由判断矩阵A(k)的一致性程度和A(k)与A(l)(k≠l)相似程度决定，记由A(k)一致性程度确定的专家的影响力为客观权重αk，由A(k)与A(l)(k≠l)相似程度决定的专家影响力为客观权重βk。

1.1 ω(k)的确定

ω(k)由对数最小二乘法[5]获得，计算公式如下:

(1)

1.2 αk的确定

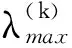
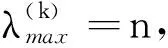
(2)

1.3 βk的确定

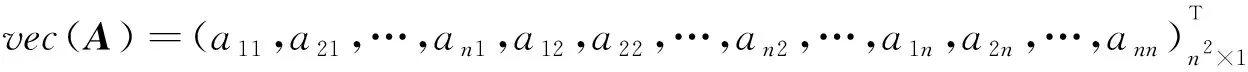
若导出向量vec(A(l))与vec(A(k))之间的夹角为θlk，则其夹角余弦为:

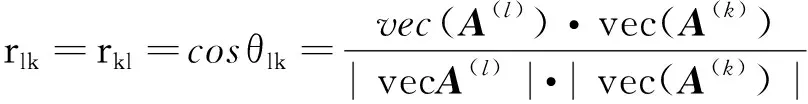
(3)

l=1,2,…,m;k=1,2,…,m;l≠k

夹角余弦rlk描述了两个导出向量vec(A(l))与vec(A(k))的相似性程度，即判断矩阵A(l)与A(k)的相关程度。rlk越大，则θlk越小，说明专家El与Ek的相似性越强，因此表示专家E(k)与其他专家一致性程度之和的平均值，即专家判断矩阵的平均一致程度为:

(4)

Rk值越大，说明Rk越能代表大多数专家的判断意见，因此，专家的客观权重βk可表示为:

(5)

因此，专家E(k)的客观权重可表示为αk与βk的凸组合，即:

γk=tαk+(1-t)βk,k=1,2,…,m

(6)

式中，0≤t≤1。

1.4 权重的聚合

由以上分析可知，γk客观权重能全面反映决策者E(k)在群决策过程中的影响力，因此，需要对指标权重ω(k)可进行修正聚合得到综合权重:

(7)

2 算法步骤

2.1 判断矩阵群的获取

群决策的基础是要获得各位专家对决策问题的判断矩阵群，判断矩阵群是经由多位不同职业的相关学科专家填表咨询之后形成的。判断矩阵的表格填写不仅要遵循AHP元素两两对比时重要性等级赋值原则，同时需要注意避免构造出“A比B 重要，B比C重要，C比A重要”有悖于常理的判断矩阵。

2.2 判断矩阵的一致性检验

按公式(8)计算各判断矩阵的萨迪(Saaty)一致性比率CR[5]

(8)

其中，λmax为判断矩阵的最大特征值，RI为随机一致性指标均值，5阶矩阵的RI等于1.118 5，如果CR<0.1，则一致性检验通过，否则需要调整判断矩阵，重新检验，直至满足要求为止。

2.3 权重的计算与聚合

采用对数最小二乘法得到指标权重ω(k)[5-7]，专家权重αk、βk分别用式(2)、(5)计算，指标权重和专家权重用式(7)进行聚合。

2.4 综合排序

对标准化后的多指标决策问题根据综合权重进行排序，对于极大值问题，综合得分越高，排序越优。

3 实例分析

建立某小口径火炮的经典内弹道模型[2]，选定装填密度Δ和相对装药量Ω为设计变量，炮膛最大压力pm、炮口速度vg、炮口压力pg、有效功率γg及炮膛工作容积利用率ηg为指标集，编程计算得到满足最大膛压小于350 MPa、初速大于980 m/s 要求的31个弹道方案如表1所示。

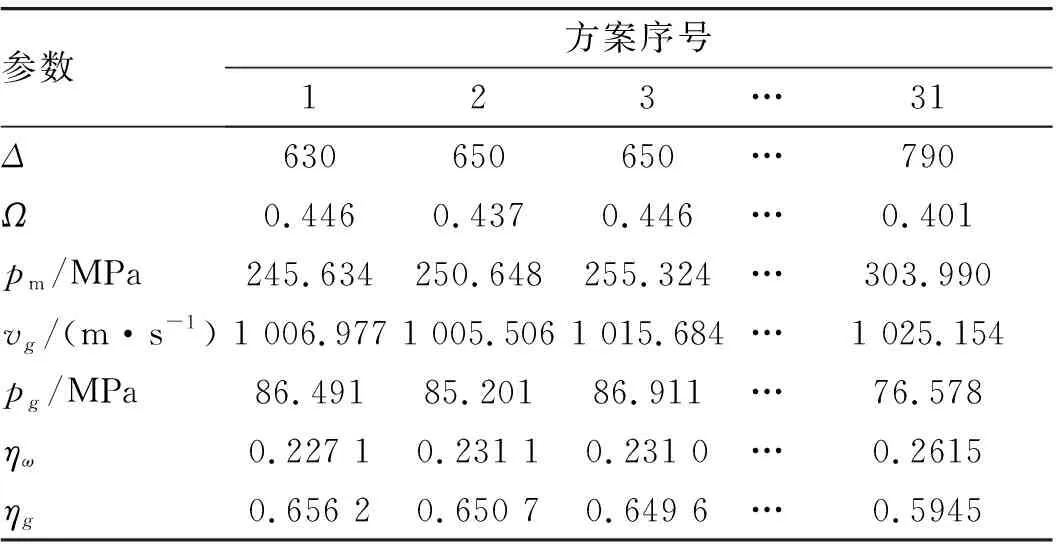
表1 方案数据表

假定四个专家的判断矩阵分别为：

按公式(8)计算的一致性比率为：

各判断矩阵的一致性比率均小于0.1，通过检验。

由对数最小二乘法得到主观权重向量ω(k)分别为:

分别按式(2)、(5)、(6)和(7)计算得到:

对决策矩阵进行规范化，由综合指标对规范化决策矩阵进行线形加权综合，得到综合指标及弹道方案排序结果如表2所示。

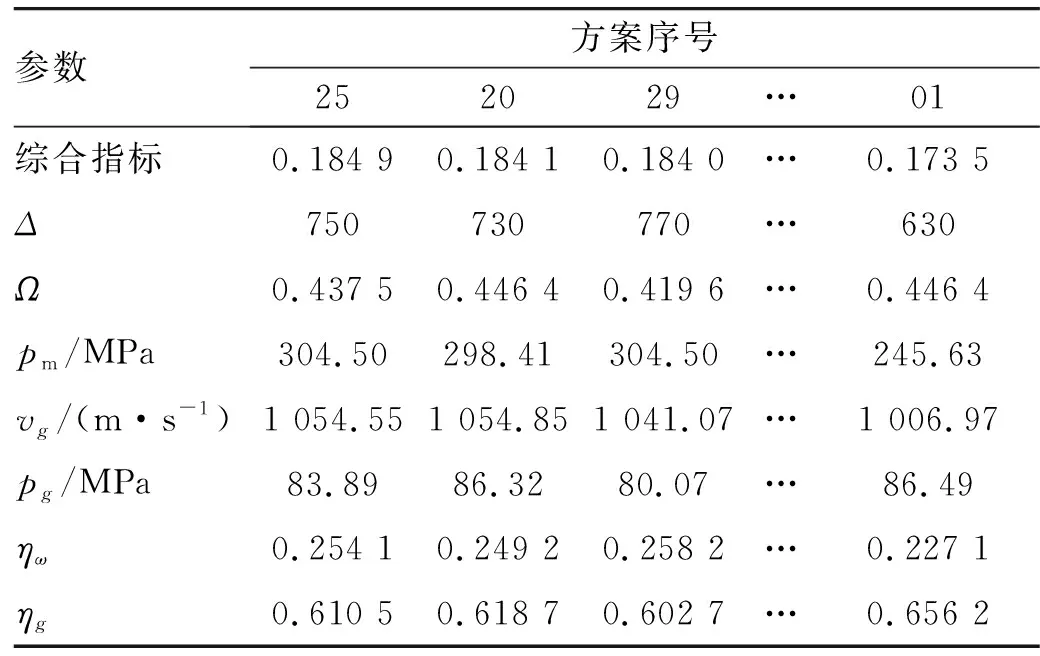
表2 综合指标及排序结果

4 结论

将火炮内弹道设计的计算过程与评价过程相结合，并将评价过程作为一类多指标群决策问题来处理。在传统弹道方案评价指标的基础上，建立火炮内弹道多指标决策模型，编程计算获得31个满足给定条件的可行弹道方案；(模拟)获得四名专家(决策者)的判断矩阵，对可行方案集进行AHP群评价。

该方法通过分析判断矩阵的一致性和相似性，获得专家权重，客观地量化了决策者在决策过程中的影响力，使得群决策过程中决策者的集体智慧得以更加客观充分地发挥，评价结果更具科学性和权威性。此方法的关键是专家判断矩阵的获取，如何诱导专家给出合理的判断矩阵，是评价结果是否科学的关键。在获得可靠的专家判断矩阵后，利用本文提供的多指标决策模型可以得到火炮内弹道方案优化结果，对提高火炮内弹道设计效率具有重要意义。

[1] 金志明，袁亚雄．现代内弹道学[M]．北京：北京理工大学出版社，1992．

JIN Zhi-ming，YUAN Ya-xiong．Modern interior ballistics[M]．Beijing：Beijing Institute of Technology Press，1992．(in Chinese)

[2] 王敬，季新源，袁亚雄．火炮内弹道设计方案多指标辅助优化分析[J]．火炮发射与控制学报,2005(2):9-12．

WANG Jing，JI Xin-yuan，YUAN Ya-xiong．Multiple attributes optimization design of gun’s interior ballistics[J]. Journal of Gun Launch & Control,2005(2):9-12．(in Chinese)

[3] 王敬，陈志武．基于熵权的火炮内弹道优化设计[J]．火炮发射与控制学报,2009(12):58-60．

WANG Jing，CHEN Zhi-wu．Optimization design of gun interior ballistics based on information entropy[J]．Journal of Gun Launch & Control,2009(12):58-60．(in Chinese)

[4] 王敬．基于方案满意度的火炮内弹道优化设计[J]．弹箭与制导学报,2011(8):133-135．

WANG Jing．An optimal design based on satisfactory degree of gun’s interior ballistics[J]．Journal of Projectiles，Rockets，Missiles and Guidance,2011(8):133-135．(in Chinese)

[5] 秦寿康.综合评价原理与应用[M].北京：电子工业出版社，2003.

QIN Shou-kang. Principle and application of comprehensive evaluation[M]. Beijing: Electronics Industry Press，2003.(in Chinese)

[6] 邓寿年, 张伟. 基于AHP群决策的国家竟技体育实力的综合评价研究[J]. 安徽工程大学学报,2011(3):81-84.

DENG Shou-nian, ZHANG Wei. Comprehensive evaluation for the strength of national sports based on AHP group decision[J]. Journal of Anhui Polytechnic University,2011(3):81-84.(in Chinese)

[7] 宋光兴，邹平.多属性群决策中决策者权重的确定方法[J].系统工程,2001(7):84-89.

SONG Guang-xing, ZOU Ping. The computing method of decision maker′s weight in multi-attributes group decision[J].Systems Engineering,2001(7):84-89.(in Chinese)