火炮发射时弹丸初速跳角数学描述及试验分析

米粮川，刘 敏，高树滋

(1.齐齐哈尔大学,黑龙江 齐齐哈尔 161006; 2.西北机电研究所,陕西 咸阳 712099;3.南京理工大学,江苏 南京 210094)

火炮的威力是火炮在战斗中迅速而准确地歼灭(毁伤)或压制目标的能力,是一个与弹、炮、药三要素密切相关的多维向量函数,通常包括射程、射击精度、火力密度、弹丸对目标的毁伤效能等要素,其中射击精度是一个关键参数。射击精度越高,对目标的毁伤概率就越大。影响火炮射击精度的因素众多, 这些影响因子的相对权重，尚未见全面的定量的研究成果。其中跳角的随机散步误差是火炮研究领域特别关注的一个影响因子。本文在参考国内外相关文献基础上，对火炮发射时弹丸初速跳角误差进行了较为系统全面的数学描述，同时对火炮射击试验过程中产生的现象进行了系统的总结与分析，对火炮武器系统工程研制具有一定的指导意义[1]。

1 弹丸初速跳角误差的定义和测度

跳角误差的定义：跳角误差是弹丸初始速度方向散布相关的一个概念，粗略地认为对于每一种类型的弹药，火炮的炮口扰动是相同的，炮口扰动的测度定义为火炮的瞄准方向与弹丸的实际初速方向之间的差值。这一观点的默认前提是系统误差是一个不变量。此项研究焦点集中在发射初始炮口指向与弹丸出炮口时的弹丸速度指向之间的偏差[2]。

采用相对大地坐标系的射角散布的数理统计评价跳角误差。如图1所示，弹丸出炮口时,弹丸沿炮膛轴线方向的线速度与垂直于炮膛轴线方向的线速度分量的矢量之和为弹丸的初速。假设射面与大地坐标系yOz坐标平面重合,高低和方向的瞄准定位误差为0。

v0=vx+vy+vz

(1)

式中:v0为弹丸相对大地坐标系的初速;vz为弹丸沿炮膛轴线方向的初速分量;vx为弹丸沿垂直炮膛轴线方向的初速分量的水平面上的投影;vy为弹丸沿垂直炮膛轴线方向的初速分量的铅垂面上的投影。

(2)

式中:θx为相对大地坐标系弹丸方向射角在xOz坐标平面上的投影;θx0炮口指向在xOz坐标平面上的投影;θy相对大地坐标系,弹丸初速方向射角在yOz坐标平面上的投影;θy0为炮口指向在yOz坐标平面c上的投影。

弹丸初速方向相对于瞄准方向的误差以θ表示,即θ为初速的方向误差，它是二维随机变量，可表示为:

(3)

θ的均值为:

(4)

任一弹丸初速方向相对于散布中心的误差θr为:

(5)

式中:θxr、θyr为散布误差在水平面上的分量和铅垂面上的分量;θr反映了弹丸初速方向的密集度[3]。

弹丸初速方向相对于瞄准方向的误差由两部分组成，即初速方向定常误差和散布误差。初速方向定常误差是弹丸平均初速方向或散布中心对瞄准方向的误差，它对应射击精度的准确度；初速方向定常误差是在决定初速诸元时产生的，当用同一初速诸元射击时，它是不论发射多少发射弹都要重复的误差，属于火炮武器系统的系统误差。弹丸初速方向散布误差是射弹的任一初速方向对初速散布中心的误差，它对应射击精度的密集度；初速方向散布误差是每发射弹都各自独立的误差，为随机误差[4]。

2 弹丸初速跳角误差散布的统一数学模型

弹丸初速随机散布误差分布的数学模型：弹丸初速散布误差是由射击过程中发与发之间射击条件的微小差异引起的。一般认为误差在起落和回转上相互独立且服从二维正态分布，假设弹丸初速散布误差服从二维正态分布，设诸元误差在铅垂方向和水平方向上相互独立，则其概率密度函数为:

(6)

(7)

3 弹丸初速跳角误差的试验探究

弹丸初速方向散布误差则是由内弹道过程中火炮系统产生的完全偶然、不可预知的误差和干扰造成的，其具有本征的随机性质。

根据火炮千米立靶的大量射击试验总结如下:

弹丸初速方向误差用瞄准方向与弹丸初速方向之间的位移向量表示,其中瞄准方向是经过重力修正的瞄准方向.给出两个随机变量特征量标准偏差刻画散布中心,标准偏差刻画散布范围。

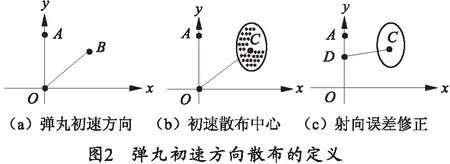
A点为瞄准具瞄准方向;O点为加入重力偏移后的炮口指向;AO为重力导致的射角变化量;B为某一发弹丸初速方向,其坐标描述如图2(a)所示;C为初速方向的散布中心点，其周围的区域为弹丸初速方向的散布范围;AD为射向误差的计算机修正量,如图2(c)所示。火炮将AD加在控制系统中,对各种弹丸类型给予误差补偿。对于某一火炮,其实不同时间和不同射角的发射,AD也是不同的。

对于某一门火炮的不同射击组次的系统默认的初速方向定常偏差一般散布是集中于一定的区域上的,如图2(a)所示,但对于多门同类型的火炮的系统默认的初速方向定常偏差一般散布是分散在一个较大的区域上的,如图2(b)所示。

鉴于上述原因,将某一型号火炮的系统默认的初速方向定常偏差定义为大量身管样本试验结果的均值偏差。系统默认的初速方向定常偏差,以下简称系统定常偏差。一定温度条件下, 一门和多门火炮的不同射击组次的系统默认的初速方向定常偏差如图3所示;不同温度条件下如图4所示。

4 结束语

火炮的系统定常偏差和散布误差按来源将其分为两类，第1类系统定常偏差是温度的函数,第2类系统定常偏差与火炮的结构参数有关。通过火炮发射时弹丸初速跳角的数学模型描述和试验数据分析，火炮发射时弹丸的跳角散布同样也要分为两类, 一类与温度有关, 另一类与火炮的结构参数有关, 在进行火炮的跳角试验研究时分清两个误差源区别对待, 对于解决火炮最大射程地面密集度这一重要的火炮战技指标问题有着较为重要的意义[6]。

[1] 王兆胜. 远程炮武器系统射击精度研究与射击精度战技指标论证[D].南京:南京理工大学, 2003.

WANG Zhao-sheng. The Study of firing accuracy and firing accuracy tactical & technical requirement reasoning for long range gunnery system[D].Nanjing:Nanjing University of Science & Technology,2003.

[2] ERIC GAGNON, MARC LAUZON. Manueuverability analysis of the conventional 155mm gunnery projectile[C]//AIAA Guidance, Navigation and Control Conference and Exhibit.San Francisco:[s.n.],2007.

[3] JAMES M GARNER, BERNARD J GUIDOS, KEITH P SOENCKSEN, et al. Flat fire jump performance of a 155mm M198 howitzer[C]//The 38th Aerospace Science Meeting & Exhibit.Nevada:[s.n.], 2000.

[4] 杨伯忠. 射击精度模型及其在火炮仿真中的应用[D].南京:南京理工大学, 2001.

YANG Bo-zhong. Firing accuracy models and its application in the howitzer simulation[D].Nanjing:Nanjing University of Science & Technology, 2001.

[5] 数学手册编写组. 数学手册[M]. 北京:高等教育出版社, 2001.

Compiling Group of Handbook of Mathematics.A handbook to mathematics[M]. Beijing: Higher Education Press, 2001.

[6] TAM T NGUYEN,ROBERT J. Spear: Approaches to reducing the temperature sensitivity of propulsion systems for artillery ammunition[R].Melbourne:Aeronautical and Maritime Research Laboratory，2011.