MEMS-SINS/GPS的组合导航在弹道修正中的应用研究

刘文逸，吴小役，范 薇，陈晓明

(西北机电工程研究所，陕西 咸阳 712099)

1 基于MEMS组合导航系统的技术特点

根据接收到的卫星信号解算出航行器的位置和速度，其误差是有界的，具有良好的长期稳定性。但是其在高动态环境下容易失锁，或者丢失信号，信号更新速率低等缺点[1]。

捷联惯导系统具有精度高、自主性强、隐蔽性好、结构简单、可靠性好、体积小、质量小、成本低、容易维修等优点，但是捷联系统中的惯性器件直接安装在载体上，载体的振动和高机动会给惯性系统带来动态误差，而且其定位误差随时间积累，无法长时间工作[2]。

随着MEMS技术发展，微惯性导航器件体积越来越小，精度也在不断提高。基于MEMS技术的SINS和GPS构成的组合导航系统，不仅结合了GPS高精度和误差不随时间积累的特点，还结合了惯导的自主性和实时性的优点，使导航系统体积减少，成本降低，可靠性增加，精度提高， 这就使得利用MEMS技术构建微型、低成本弹载的SINS/GPS组合导航系统越来越成为一种发展趋势。

基于MEMS的SINS/GPS组合导航技术通常由微惯性测量单元、导航计算机、GPS接收模块、电源构成[2]。SINS由3个MEMS单自由度陀螺仪和一个三轴MEMS加速度计构成，弹载组合导航系统结构如图1所示。

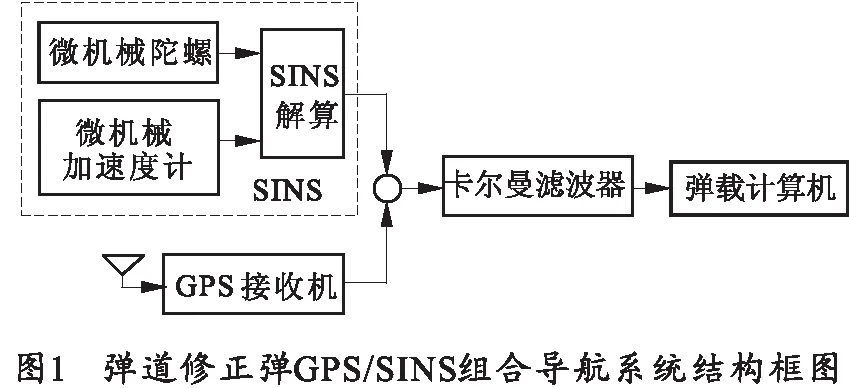
2 数学模型的建立及仿真分析

2.1 MEMS-SINS误差模型

1)数学平台误差方程

误差角方程为:

(1)

式中:Φ为平台失准角；ε为等效陀螺仪漂移,其他符号含义见文献[2]。

2)位置误差方程

(2)

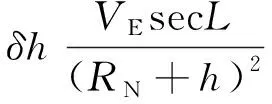
(3)

(4)

3)速度误差方程

可根据比力方程求微分得到：

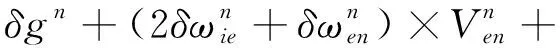
(5)

2.2 微惯性传感器的误差模型

安装在弹体上惯性器件存在误差，对系统影响较大的误差源是惯性器件误差和安装误差，其中安装误差可以通过提高安装精度和安装误差标定等手段进行补偿。

1)微型陀螺仪误差模型

本文采用的是精度较低的微型陀螺和加速度计，仅考虑零偏、马氏过程误差及白噪声[2]。

ε=εb+εr+ωg

(6)

式中:εb为随机常数；εr为一阶马尔柯夫过程；ωg为白噪声，其方差为δ2。

2)加速度计误差模型

加速度计是另一重要惯性测量元件，用于测量载体的线运动参数(比力)[2]。

考虑主要误差项，其误差模型为：

=b+ωa+r

(7)

3 组合导航模型及其仿真分析

3.1 系统状态方程

本文是以修正弹为研究背景的，在满足其导航精度前提下，对模型作了一些简化，选取了18个SINS状态作为滤波器的状态;9个SINS系统误差(3个姿态误差、3个速度误差及3个位置误差)；3个陀螺的常值漂移；3个陀螺的随机误差；3个加速度计的零位误差[3]。因此，组合导航系统位置速度组合模式下的状态方程为：

(8)

其中，状态变量一共18维如上所述，

XI=[φEφNφU∂VE∂VN∂VU∂L

(9)

噪声矩阵为：

W(t)=[ωgxωgyωgzωbxωbyωbzωax

ωayωaz]T

(10)

式中，元素依次为3个陀螺仪随机白噪声漂移、3个陀螺仪一阶马尔科夫驱动白噪声和3个加速度计一阶马尔科夫驱动白噪声[2]。

相应的白噪声方差阵Q(t)为 :

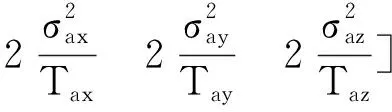
(11)

系统状态转移矩阵及噪声系数矩阵分别为：

(12)

(13)

3.2 系统量测方程

SINS/GPS组合导航系统的选择位置、速度组合模式。系统量测值包括：位置量测差值、速度量测差值。

定义位置量测差值为：

(14)

定义速度量测差值为：

(15)

将位置量测差值与速度量测差值综合在一起，可得：

H(t)X(t)+V(t)

(16)

式(16)为综合系统的量测方程。

3.3 卡尔曼滤波器设计

对上述的系统状态方程和量测方程进行离散化可得：

Xk=Φk,k-1Xk-1+Γk-1Wk-1

(17)

Zk=HkXk+Vk

(18)

式中：Φk,k-1为tk-1时刻至tk时刻的一步转移阵；Γk-1为系统噪声驱动阵；Hk为量测噪声序列；Wk为系统激励噪声序列[3]。

同时，Wk和Vk满足:

E[Wk]=0

E[Vk]=0

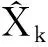
状态一步预测：

(19)

状态估计：

(20)

滤波增益：

(21)

或

一步预测均方误差：

(22)

估计均方误差：

(23)

或

Pk=(I-KkHk)Pk/k-1

或

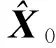
3.4 仿真与分析

SINS/GPS组合导航系统主要包括弹道解算模块、捷联惯导仿真器、GPS模拟仿真器、导航计算模块，卡尔曼滤波模块[4]。仿真机构如图2所示。

由于条件限制，无法得到实际飞行仿真数据，因此，本文采用一种纯数学方法产生捷联惯导仿真系统测试用的飞行轨迹数据。该测试用的飞行轨迹发生器提供载体的3个独立的姿态角时间函数及姿态角变化率时间函数和载体在导航坐标系中的3个轴向的速度时间函数及加速度时间函数，虽然该轨迹发生器产生的数据不是实际飞行轨迹[5-6]，但是可以用来验证SINS/GPS组合导航系统的精度是否能够满足弹道修正弹导航定位精度[7]。本文惯性器件仿真模块原理可见参考文献[7],捷联解算采用四元数方法，即用四阶龙格-库塔法求解四元数的微分方程[3,7]。仿真初始条件：仿真初始纬度为38°，经度为125°，初始位置误差10m,初始速度误差为0.5 m/s,初始平台误差角为0.2°，陀螺漂移为0.005(°)/s,加速度计漂移为0.004g， GPS接收机位置误差分别为10、10和15 m,速度误差为0.5 m/s。卡尔曼观测更新为每1 Hz采用GPS与SINS差作为输入更新值，由此得到卡尔曼滤波校正值。

根据上述简易修正弹组合导航方案运用MATLAB进行了数值仿真计算，分别得到纯MEMS惯性导航系统和组合导航系统的位置、速度误差曲线图，仿真结果见图3～图6。

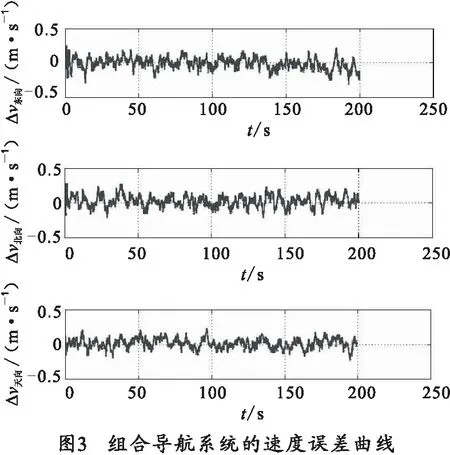
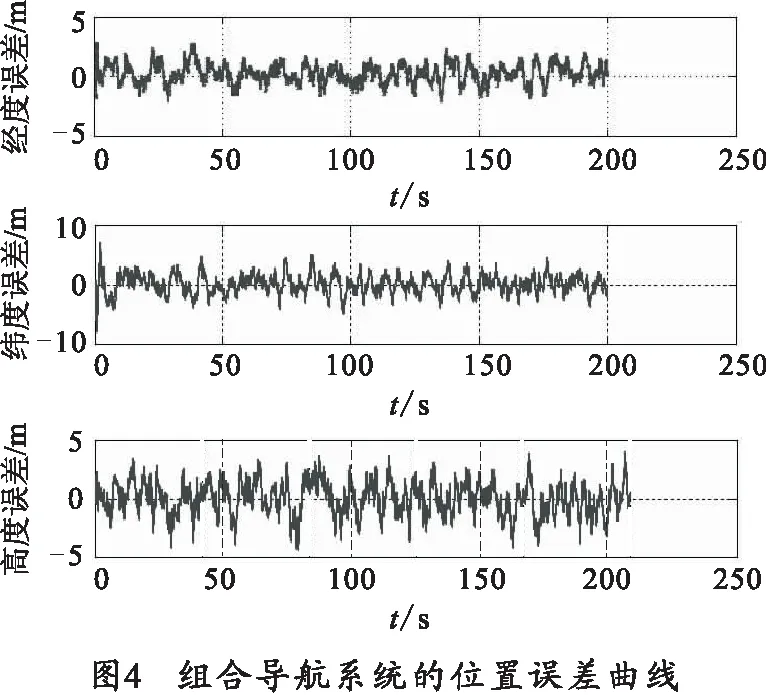
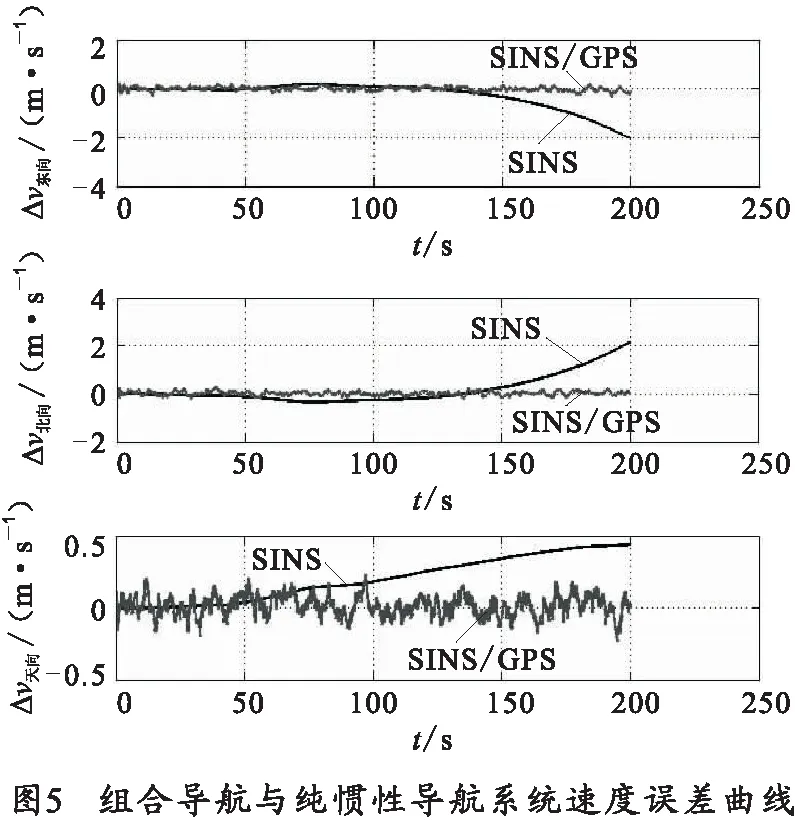
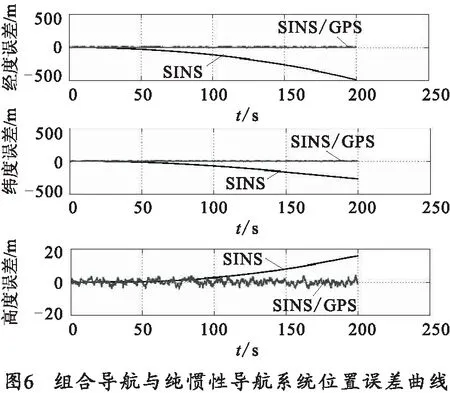
图3为组合系统的东北天方向速度误差曲线图，从图上可以看出东向、北向和天向速度误差都在0.5 m/s以内，图4为组合系统的位置误差曲线图，从图中可以得到位置误差都在5 m之内，图5和图6给出了SINS系统和经过GPS校正的SINS系统的速度和位置误差仿真结果，从图中可以看出SINS单独工作时，速度、位置误差均随时间增长，而经过GPS校正后，SINS的输出误差明显减少，并且不随时间增长。从而从理论上验证了基于MEMS的组合导航系统在弹道修正弹上应用的可行性和有效性。

4 跑车试验与结果分析

为了评估本文研究的组合导航系统导航性能，在公路上对原理样机进行了跑车动态试验。将组合导航仪安装到汽车顶部，利用原理样机对行驶中的汽车位置和速度进行实时解算。试验后，将黑匣子记录到的惯导和GPS等传感器原始测量数据注入仿真模型，对组合导航的滤波算法进行验证，仿真结果如图7和图8。

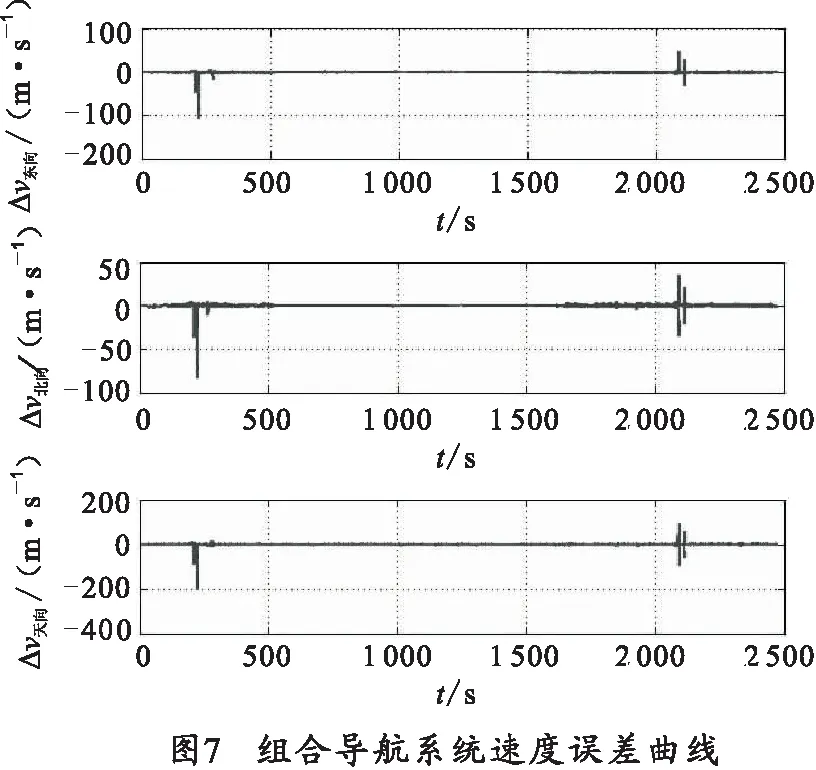
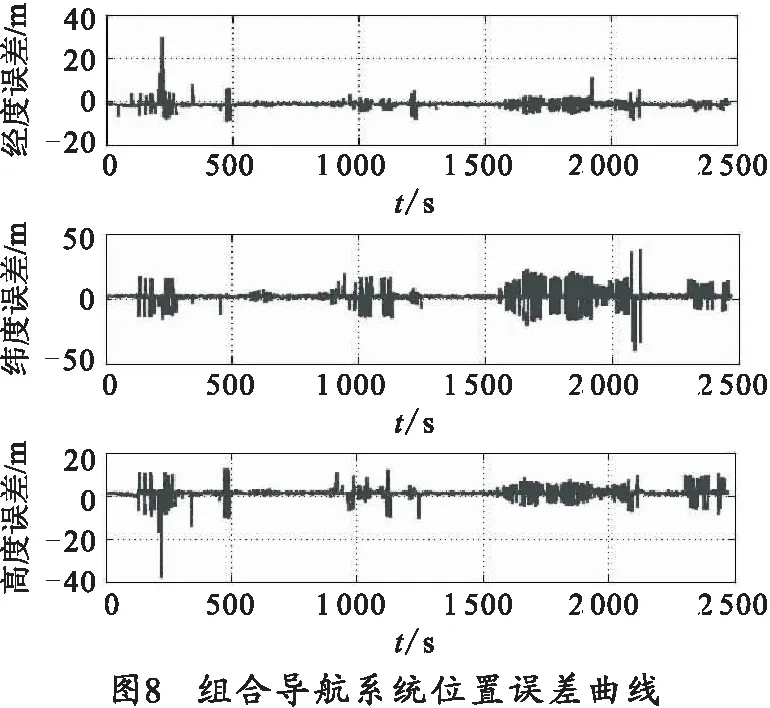
图7给出了组合导航系统东北天向速度误差；图8给出了组合导航系统经纬高度位置误差。其图表明，GPS速度、位置信息的引入大大提高了系统的导航精度。

5 结 论

本文以修正弹为研究对象，运用MATLAB分别对SINS和组合导航系统进行了数值仿真，仿真结果从理论上验证了基于MEMS器件的低成本组合导航系统在弹道修正中应用的可行性和有效性；并通过跑车试验对该组合导航系统的滤波算法进行了试验验证。仿真计算与跑车试验结果表明，该组合导航系统能提供高精度的位置和速度信息，进而为弹道修正控制机构提供精确的测量信息，提高修正弹的打击精度,因此，该研究具有一定的工程应用价值。

[1] 秦永元.惯性导航[M].北京：科学技术出版社，2006.

QIN Yong-yuan.Inertial guidance[M].Beijing: Science Press，2006. (in Chinese)

[2] 王惠南.GPS导航原理与应用[M].北京:科学出版社,2003.

WANG Hui-nan.Principles and applications of GPS navigation[M].Beijing:Science Press,2003. (in Chinese)

[3] 秦永元,张洪钺,汪叔华.卡尔曼滤波与组合导航原理[M].西安：西北工业大学出版社,1998.

QIN Yong-yuan,ZHANG Hong-yue,WANG Shu-hua.The Kalman filter and integrated navigation technology[M]. Xi’an: Northwestern Polytechnical University Press, 2008.(in Chinese)

[4] MILLER I, SCHIMPF B, CAMPBELL M, et. al. Tightly-coupled GPS/INS system design for autonomous urban navigation[C]//Berlin:Position, Location and Navigation Symposium, 2008:1297-1310.

[5] 吴太旗，孙付平，易维勇，等.GPS/INS组合导航系统的MATLAB/Sinmulink仿真[J].测绘学院学报，2004，21(3):172-174.

WU Tai-qi,SUN Fu-ping,YI Wei-yong.Simulation on integrated GPS/INS navigation system using matalab/simulink[J].Journal of Institute of Surveying and Mapping,2004,21 (3):172-174. (in Chinese)

[6] 许国珍,吴美平.低成本MIMU/GPS组合导航研究[J].计算机仿真,2008,25(10):69-72.

XU Guo-zhen,WU Mei-ping.A low cost MIMU/GPS integrated system[J].Computer Simulation, 2008,25(10): 69-72. (in Chinese)

[7] 齐鑫,秦永元,朱新颖,等.基于MATLAB/SIMULINK的捷联惯性导航系统仿真[J].计算机测量与控制, 2008:16 (8): 61-64.

QI Xin,QIN Yong-yuan,ZHU Xin-ying,et al. Inertial navigation system simulation base on MATLAB/SI-MULINK[J].Computer Measurement&Control,2008,16(8):61-64. (in Chinese)