面向任务的装备固有可用度试验方案
2013-11-21于永利
付 康,于永利,张 柳,徐 英,张 伟
(军械工程学院 装备指挥与管理系,河北 石家庄 050003)
固有可用度作为保障性综合设计参数,指仅与寿命和修复性维修时间有关的系统可用度,是装备使用和研制部门最关心的参数之一[1-2]。固有可用度A的一般表达式为:
A=E(X)/[E(X)+E(Y)]
(1)
式中:X表示故障间隔时间;Y表示修复时间。
面向任务的固有可用度A可表示为平均执行任务时间内,平均工作总时间U与平均总工作时间U和平均总修复时间D之和的比,即:
A=U/(U+D)
(2)
固有可用度验证试验作为验收性试验,其目的是在装备定型阶段,在规定条件下,证明固有可用度是否达到规定要求,对达到装备设计特性要求具有重要监督作用。固有可用度试验的顺利完成需要一系列技术作支撑,其中试验方案设计是最为关键的技术之一。
固有可用度试验方案研究文献情况,见表1[3-7]。当前国内外可用度试验方案的相关研究较少,主要集中在故障间隔时间和修复时间服从指数分布,且优先考虑试验经济性试验方案的研究上。满足任务需求的装备固有可用度试验方案几乎没有涉及。然而,装备通常都针对任务设计,对装备进行固有可用度验证试验,应当将任务需求和经济性综合考虑,并且应当优先考虑能否满足任务需求。因此,本文在描述相关背景和假设基础上,基于任务-装备-维修队列模型,确定固有可用度的检验估计量;并且满足给定的承制方和使用方风险的前提下,在优先考虑任务需求的基础上,综合考虑任务需求和经济性,设计试验实施过程,完成了固有可用度试验方案设计。

表1 固有试验方案研究文献情况
1 背景与假设
1) 面向任务的固有可用度试验将装备状态分为交替进行的开机与修复两种。
2)X与Y相互独立,可获得试验数据为故障间隔时间Xi与修复时间Yi,i为第i次出现故障与第i次修复。
3) 完成第j次任务前最后一次工作时间Wj。
4)X服从指数分布,E(X)=1/λ。Y服从指数分布,E(Y)=1/μ。
5) 已知固有可用度检验上下限之分别为:A=A0,A=A1;A0>A1。承制方风险为α,使用方风险为β。
6)M为单次执行任务时间,包括装备的总工作时间V和总修复时间R。V的分布函数为H(t)。E(V)=τ。执行第j次任务时间为Vj。
7)任务到达速率小于任务执行速率,即装备不需要等待任务的到来。

9)T为面向任务的固有可用度A试验的截止时间,其中装备总工作时间为U(T),总修复时间为D(T)。
2 固有可用度检验估计量的确定
笔者基于文献[8]描述的任务-装备-维修队列模型。假设完成第j次任务共发生lj次故障。执行第j次任务的时间推进图,如图1所示。

根据文献[8]对于模型的分析,已知:
D=E(R)=τλ/μ
(3)
U+D=E(V)+E(R)=τ(1+λ/μ)
(4)
再依据式(2),可得:

即得面向任务的固有可用度A的表达式为:
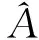
(5)
3 试验方案设计
对于固有可用度验证试验设计,需要满足给定的承制方和使用方风险。根据面向任务的固有可用度A的检验估计量表达式(5),首先需要设计定时截尾试验方案,TA为试验截止时间。
假设:H0:A=A0,H1:A=A1
需要满足的接收概率不等式组为:
(6)
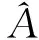
如果优先从经济性的角度考虑进行试验方案设计,可将不等式组转化为:
(7)
根据文献[5]的结论,方程组(7)可转化为方程组(8)。up为标准正态分布的上p分位点。
(8)
根据式(8),可得试验截止时间和判定临界值为:
(9)
已知0 可得,uα是TA的严格单调增函数,uβ是TA的严格单调增函数。即在C固定不变的前提下,随着TA的增大,承制方风险α和使用方风险β都会下降。因此,TA增大同样可以满足式(6)。 基于以上的分析,为了在考虑经济性的基础上,优先满足任务需求,尽可能完整地反映单次任务中故障间隔时间和修复时间的关系,可通过适当增加试验时间的办法来实现,认为检验A需要经历m次完整的任务,即完成第m任务后试验才能截止。m次任务总时间为: (10) 这里设计一种面向任务的固有可用度试验实施过程,如图2所示。 试验开始前,由定时截尾试验方案得到试验截止时间TA。试验开始后,从m=1开始,完成第m次任务,这次任务执行时间为Vm,得到任务总时间Tm。将Tm与TA作比较,如果Tm≥TA,试验停止,试验截止时间为T=Tm。如果Tm 假设:H0:A=A0,H1:A=A1。 以某型自行火炮为例,故障间隔时间和修复时间都服从指数分布。需进行面向行军任务的固有可用度验证试验,分为以下3个步骤进行。 给定:A0=90%,A1=80%;α=β=10%。利用接收概率方程组(7),可得C≈87.3%,TA≈78.1 h。 完成第1次任务,这次任务执行时间为V1=37.5 h,得到任务总时间T1=37.5 h。由于T1 在假设故障间隔时间和修复时间都服从指数分布的前提下,优先考虑装备能否满足任务需求,设计了一种面向任务的固有可用度试验方案,给装备定型阶段的试验验证工作提供了技术依据。然而,由于本文假设故障间隔时间和修复时间都服从指数分布,当故障间隔时间服从威布尔分布或修复时间服从最常见的对数正态分布时,本试验方案却不完全适用。如何克服这些问题和不足在今后的研究工作中将是重点。 [1] 甘茂治,康建设,高崎. 军用装备维修工程学[M].北京:国防工业出版社,2005. GANMao-zhi,KANGJian-she,GAOQi.Materielmaintenanceengineering[M].Beijing:NationalDefenceIndustryPress,2005.(inChinese) [2] 武小悦,刘琦. 装备试验与评价[M]. 北京:国防工业出版社,2008. WU Xiao-yue, LIU Qi. Equipment test and evaluation [M].Beijing: National Defense Industry Press, 2008. (in Chinese) [3] USHER J S,TAYLOR G D. Availability demonstration testing[J].Quality and Reliability Engineering International, 2006(22):473-479. [4] RISE J, BORKLAND. Test plan for availability[R]. Telub: AB S-85101 1972. [5] 王玲玲. 可用度的序贯验证试验方案[J]. 华东师范大学学报:自然科学版,1992,17(2): 22-30. WANG Ling-ling. Sequential test procedures of availability[J]. Journal of East China Normal University:Natural Science,1992,17(2):22-30. (in Chinese) [6] 孙祝岭. 系统稳态可用度抽样检验方案[J]. 中国空间科学技术,1996,16(3): 35-38. SUN Zhu-ling. Sampling verification plan for steady state availability of systems[J] Chinese Space Science and Technology, 1996,16(3): 35-38. (in Chinese) [7] 周正伐. 可靠性工程基础[M]. 北京:中国宇航出版社,2009. ZHOU Zheng-fa. Reliability engineering foundation[M]. Beijing: China Aerospace Publication House, 2009. (in Chinese) [8] 毕军, 王少萍,石键. 面向任务的单武器系统平均修复时间模型[J]. 北京航空航天大学学报,2007,33(3): 354-356. BI Jun, WANG Shao-ping, SHI Jian. Mean time to repair modeling oriented uni-mission for weapon system[J]. Journal of Beijing University of Aeronautics and Astronautic, 2007,33(3): 354-356. (in Chinese)

4 应用实例分析
4.1 试验前设计定时截尾试验方案
4.2 实施固有可用度试验
4.3 试验后的判定

5 结 论
