基于离散GM(1，1)模型的武器备件故障率预测研究

邵延君，马春茂，潘宏侠，刘永姜

(1.中北大学,山西 太原 030051；2.西北机电工程研究所,陕西 咸阳 712099)

武器装备由于生存的环境特殊性和设备本身的老化等因素的影响，会不可避免地出现故障,但由于武器装备复杂程度不同，使其表现出的故障规律存在较大差别[1-3]，通过对大量故障数据进行统计分析后，可以得到故障率随时间变化的典型的故障率曲线，典型的故障率λ(t)随工作时间t的变化趋势具有3个明显的区域，人们形象地把它称为“浴盆曲线”[4]。早期故障期的故障率呈逐渐下降的趋势;偶然故障期的故障率接近于常数;耗损故障期的故障率呈逐渐上升趋势。通过对典型的故障率曲线进行分析，发现早期故障期和耗损故障期的故障率λ(t)随时间呈非线性变化，于是考虑用GM(1，1)模型对早期故障期和耗损故障期两个阶段的故障率进行预测，GM(1，1)模型对于非线性序列进行预测具有一定的优势，但是传统的GM(1，1)模型对非线性序列预测存在较大误差，离散GM(1，1)模型则能够比较精确模拟非线性序列，因此考虑用离散的GM(1，1)模型对武器备件的故障率进行预测[5-6]。

1 GM(1，1)建模

2)对生成的序列X(1)(t)有如下一阶线性白化微分方程dx(1)/dt+ax(1)=b，当t取单位时间时，一阶微分方程的差分形式等于微分形式，dx(1)/dt=x(1)(t+1)-x(1)(t)=x(0)(t)，所以GM(1，1)模型的微分方程可以表示为：x(0)(t) +ax(1)(t)=b，称为GM(1，1)模型的原始形式。

3)为了使一次累加生成序列更平滑，对X(1)作紧邻均值生成。Z(1)=(z(1)(2),z(1)(3),z(1)(4),…,z(1)(n))，其中z(1)(t)=0.5(x(1)(t)+x(1)(t-1))，x(0)(t)+aZ(1)(t)=b为GM(1，1)模型的基本形式。式中：a为发展系数；b为灰作用量；Z(1)为X(1)的紧邻均值生成序列。

4)对GM(1，1)模型的基本形式的参数a、b进行求解。a和b的数值通过最小二乘法估计得到:

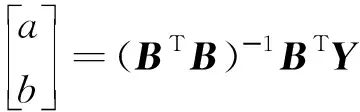
(1)

t=1，2，…，n-1

(2)

6)进行累减还原得:

t=1，2，…，n-1

(3)

2 建立离散的GM(1，1)模型

1)设X(0)为非负原始序列，对原始序列X(0)进行一次累加生成,得到新的数据列X(1)，建立离散的GM(1，1)模型为：

x(1)(t+1)=β1x(1)(t)+β2

(4)

2)利用最小二乘法估计离散GM(1，1)模型中的参数β1和β2，得:

(5)

Y=[x(1)(2),x(1)(3),…,x(1)(n)]T

3)将β1和β2的值代入离散GM(1，1)模型的递推函数得：

(t=1，2，…，n-1)

(6)

4)进行累减还原

(t=1，2，…，n-1)

(7)

3 实例分析

某装备修复性的维修任务均由某军械维修保障中心负责,所有备件的维修和更换均通过该维修保障中心,军械维修保障中心的数据可以客观准确地反映备件更换和损耗量情况。通过对某武器备件的资料查阅，可知某武器备件损耗期的故障率，表1是近6年某武器备件在正常使用情况下损耗期的故障率，从表中的数据可以看出,备件损耗期的故障率在损耗期呈现出明显的增加趋势,下面利用上述的两种灰色理论模型对故障率进行预测，其中t表示某武器备件的工作时间;λ(t)表示某武器备件的故障率。

表1 武器备件损耗期的故障率

1)取前4组数据做模拟，后面两组数据进行检验，建立GM(1.1)模型，则原始序列为：

X(0)=(x(0)(1),x(0)(2),x(0)(3),x(0)(4))=(0.15，0.334 2，0.655 0，1.115 8)，将原始数据进行一次累加生成和紧邻均值生成后,得到B和Y的值为:

利用MATLAB软件,带入B和Y计算，可以得到a和b的值为:a=-0.420 774，b=0.248 07，将a和b的值代入时间响应函数(2)得到：

利用公式(3)做累减还原得到GM(1，1)模型对原始序列的模拟值:

2)取前4组数据做模拟，建立离散GM(1，1) 模型，后面两组数据进行检验，将原始数据进行一次累加生成后,得到B和Y的值为:

利用MATLAB软件,带入B和Y计算，可以得到β1和β2的值为：β1=1.532，β2=0.314,将β1和β2的值代入离散GM(1，1)模型的递推函数(6)得到：

利用公式(7)做累减还原得到离散GM(1，1)对原始数据的模拟值:

检验其精度，列出两种模型的误差检验表如表2所示。

表2 模型误差检验表

通过上述实例的平均相对误差的结果比较可知，虽然两种方法都可以进行故障率的预测，但是可以知道离散的灰色GM(1，1)模型较传统的灰色GM(1，1)模型对典型的故障率预测精度有所提高。

4 利用两种预测模型对故障率进行中长期预测

下面利用离散的灰色GM(1，1)模型的递推函数和灰色GM(1，1)模型的时间响应函数对后两年的故障率进行预测，并对预测的结果与实际值比较，计算的结果如表3所示。

从模型的预测结果看，灰色模型只需要4组数据就可以对故障率进行中长期预测,体现了灰色理论在预测方面的优势。

表3 故障率中长期预测表

5 结 论

本文针对复杂武器备件的故障率预测的难点，通过对典型的故障率曲线研究的基础上，利用灰色理论在“少数据”、“贫信息”、“不确定性”预测问题中的优势，在传统的灰色GM(1，1)模型的基础上提出了利用离散的灰色GM(1，1)模型对武器备件故障率进行预测，最后利用两种不同的模型对某武器备件故障率进行了预测，通过结果比较和验证，可知离散的灰色GM(1，1)模型是武器备件的故障率预测的一种有效方法。

[1] 马秀红,宋建社,董晟飞.基于回归分析的备件故障率预测模型[J].计算机仿真，2003，20(11)：6-8.

MA Xiu-hong，SONG Jian-she，DONG Yan-fei. Model of spare parts failure rate based on linear regression[J]. Computer Simulation, 2003，20(11)：6-8.(in Chinese)

[2] 许绍杰，谭贤四，王晗中，等.基于多因素不等时距灰色模型的雷达故障预测[J].现代雷达，2011，33(8)：26-28.

XU Shao-jie,TAN Xian-si, WANG Han-zhong，et al. A mugm(1，m，w) model of radar fault prediction[J]. Modern Radar, 2011，33(8)：26-28.(in Chinese)

[3] 董晟飞,马秀红.基于回归分析的故障率预测模型[J].可靠性技术，2005(5):28-29.

DONG Yan-fei, MA Xiu-hong. Study on failure rate prediction model based on linear regression[J].Reliabi-lity Technology, 2005(5)：28-29.(in Chinese)

[4] 甘茂治，康建设，高崎.军用装备维修工程学[M]．北京:国防工业出版社，2005:33-36.

GAN Mao-zhi,KANG Jian-she,GAO Qi. Military equipment maintenance engineering[M]．Beijing:National Defense Industry Press，2005:33-36.(in Chinese)

[5] 刘思峰，郭天榜，党耀国，等．灰色系统理论及其应用[M]．北京:科学出版社，2010:182-187.

LIU Si-feng,GUO Tian-bang,DANG Yao-guo, et al. Research and application on grey theory on cost forecasting[M]．Beijing:Science Press，2010:182-187．(in Chinese)

[6] 高钰榕,戚君宜. 维修用备件需求预测方法[J].火炮发射与控制学报,2008(4):75-78．

GAO Yu-rong,QI Jun-yi. Forecast method for maintenance spare parts requirement[J].Journal of Gun Launch & Control, 2008(4):75-78．(in Chinese)