一类不确定Lurie系统的输出反馈H∞滑模控制问题
2013-11-20周长芹孟晓玲毛北行
周长芹,孟晓玲,毛北行
(郑州航空工业管理学院 数理系,河南 郑州 450015)
滑模控制作为一种重要的鲁棒控制策略,以其响应快、对内部参数摄动和外部干扰不敏感等优点得到了广泛的应用,文献[1]研究了非匹配不确定输入时滞系统的自适应滑模控制问题,文献[2-3]研究了一类切换系统的滑模控制问题,文献[4]研究了不确定输入时滞系统的滑模输出反馈控制问题,文献[5-6]研究了Lurie混沌系统的同步控制问题.本课题研究了一类不确定Lurie系统的输出反馈H∞滑模控制问题,并证明了设计的切换面的可达性,基于Lyapunov稳定性理论给出了系统渐稳的充分条件.
1 主要结果
考虑如下的一类不确定Lurie系统
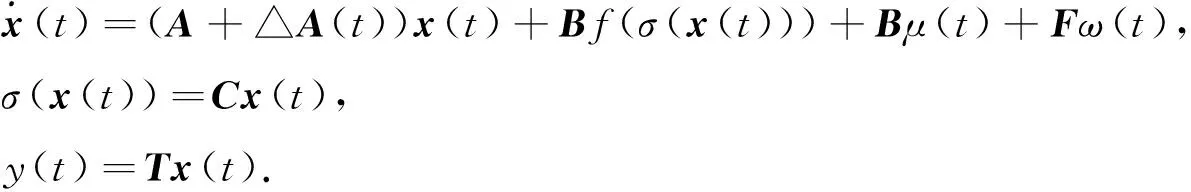
(1)
其中f(σ)位于有限的霍尔维茨角域之中:
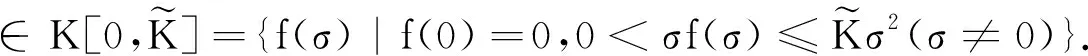
(2)
A,B,C,D,F,T为适当维数的常数矩阵,△A(t)=EF(t)H,E和H为适当位数的常数矩阵,不确定矩阵F(t)满足F(t)TF(t)≤I,
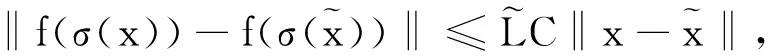
(3)

假设B列满秩,(A,B)能控,(A,C)能观.
引理1 给定适当维数的矩阵Y,D和E,F,则Y+DFE+ETFTDT<0对所有满足FFT≤I的矩阵F成立,当且仅当存在一个常数λ>0,使得Y+λDDT+λ-1ETE<0.
引理2 (Schur补引理) 设A,B,C为适当维数的矩阵,则下面3个式子等价:
(1)A<0,C-BTA-1B<0;
(2)C<0,A-BTC-1B<0;
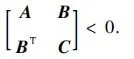
对系统(1)设计如下观测器:
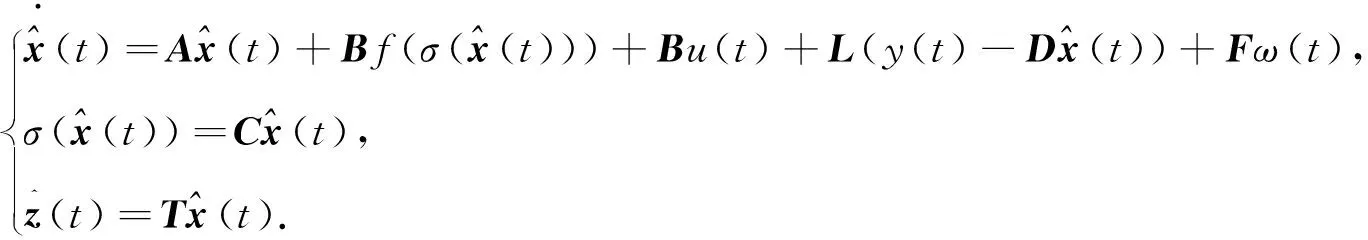
(4)
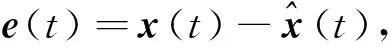
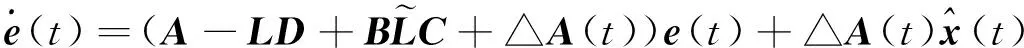
(5)
(6)
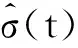
设计滑模控制律为
(7)
定理1 在满足状态观测器(4)和切换函数(6)的条件下,滑模控制律(7)能够保证系统轨迹在有限时间内到达切换面s(t)=0上,并沿着切换面运动.
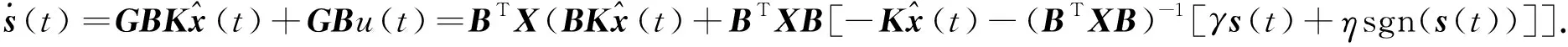
(8)
分别得到滑模动态方程和估计误差方程:
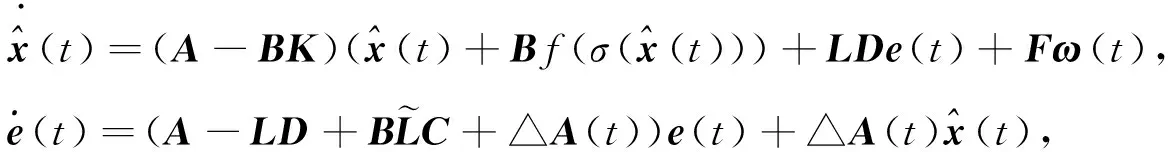
(9)
定理2 选择上述切换函数和控制律,若存在正定矩阵X,Y,标量ε1>0,ε2>0满足如下不等式:
(10)
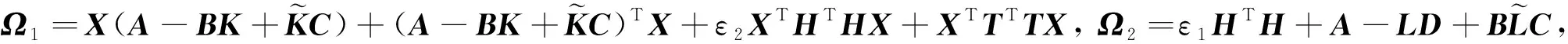
且滑模矩阵G=BTX,观测增益矩阵为L=X-1Y,则闭环系统(9)具有H∞性能指标γ.
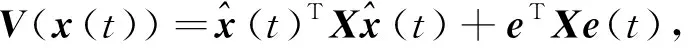
利用引理1很容易得到
(11)
(12)
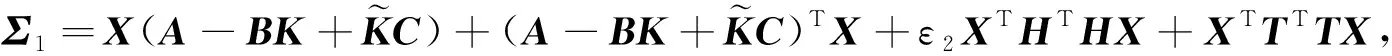
由引理2可知不等式(12)等价于不等式(10),从而系统具有H∞性能指标γ,另一方面,当ω(t)=0时,
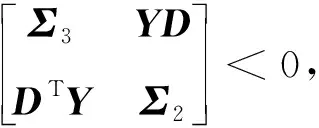
2 仿真算例
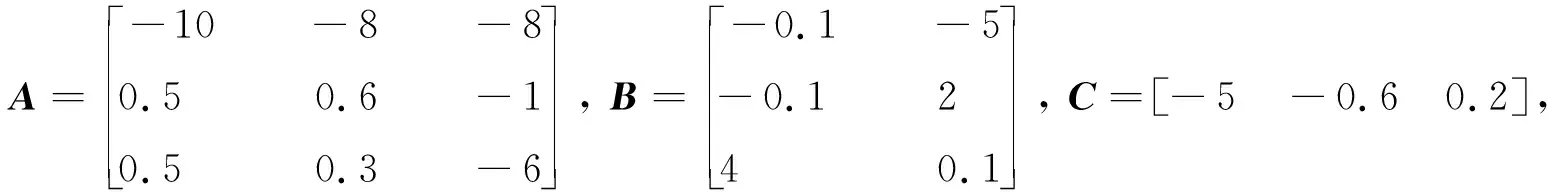
f(σ)=0.68x1+0.295(|x1+1|-|x1-1|),
E=[0.2 0.4 0.2],H=[-0.2 0.3 -2],F(t)=sint,K=[0.2 0 0.3],
通过求解线性矩阵不等式得到
ε1=0.120 4, ε2=0.231 7, ε3=0.890 5,

控制信号u(t)和系统状态x(t)的轨迹见图1和图2.
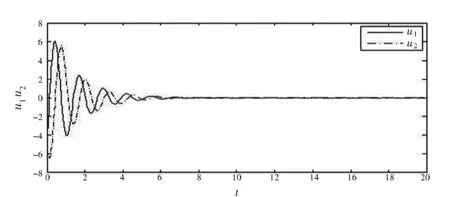
图1 控制信号u(t)的轨迹 Fig.1 Trajactories of control signal u(t)
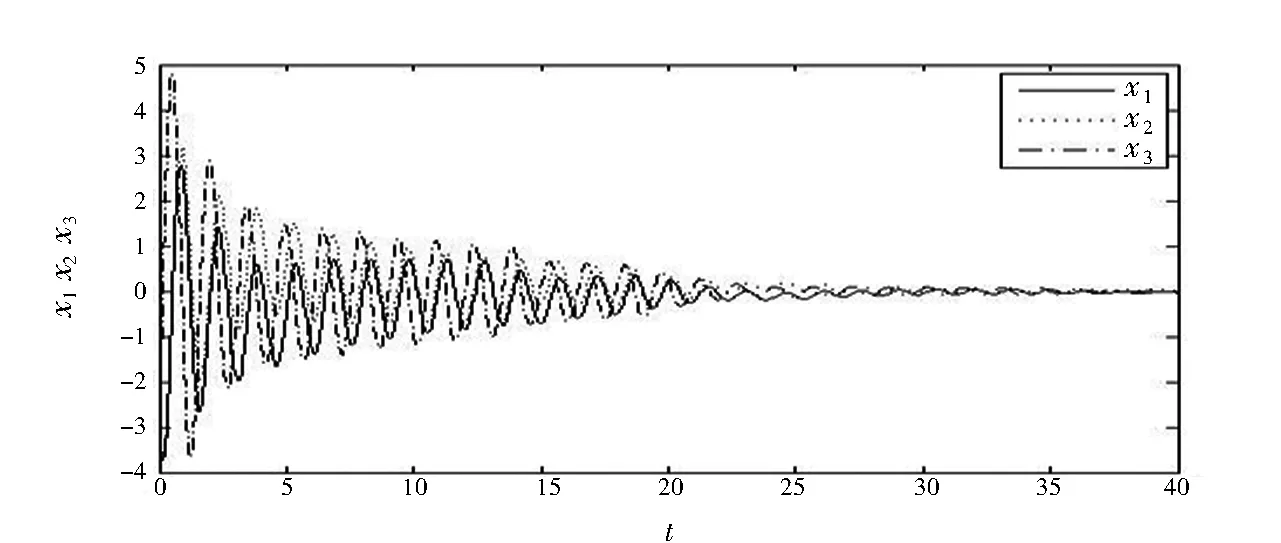
图2 系统状态x(t)的轨迹Fig.2 Trajectories of systems state estimation x(t)
3 结束语
研究了一类不确定Lurie系统的输出反馈H∞滑模控制问题,并证明了设计的切换面的可达性,基于Lyapunov稳定性理论给出了系统渐稳的充分条件.
参考文献:
[1] 王明顺,于滨,高宪文.非匹配不确定输入时滞系统的自适应滑模控制[J].东北大学学报:自然科学版,2008,29(8):1069-1072.
[2] 何召兰,王茂,崔阳.一类切换系统基于观测器的滑模降阶控制[J].控制理论与应用,2009,26(6):704-708.
[3] 何召兰,王茂,周卫宏.一类切换系统降阶输出反馈滑模控制[J].系统工程与电子技术,2008,30(10):1962-1965.
[4] 贾廷纲,牛玉刚,夏康.不确定输入时滞系统的滑模输出反馈控制[J].信息与控制,2011,40(6):809-812.
[5] 何汉林,涂建军,熊萍.一类Lurie混沌系统的全局渐近同步[J].华中科技大学学报,2010,38(2):38-40.
[6] 毛北行,王东晓,卜春霞.Lurie混沌系统的脉冲控制同步[J].华中师范大学学报:自然科学版,2012,46(3):297-299.
