Ad hoc网络中基于身份的组密钥管理方案

刘晓乐

(河南工程学院 计算机学院,河南 郑州 451191)

Ad hoc网络是一种由节点组成的多跳临时性自治系统，在军事救灾和民用通信领域都有广泛的用途.Ad hoc网络不依赖事先铺设的固定设施,具有网络的独立性、动态变化的拓扑结构、计算和存储能力有限和节点容易受到攻击等特点.Ad hoc网络自身的特殊性决定了它将面临与传统无线网络相同甚至更严重的安全问题.组密钥管理可以解决成员之间的共享密钥问题，确保合法组成员之间得到安全可靠的组密钥，故组密钥管理的研究是当前Ad hoc网络安全研究中的一个重点和难点.组密钥的管理包括组密钥的生成和维护，密钥的维护是指由于成员节点的加入和退出而需要改变密钥，或者长时间使用后需要对组密钥进行更新.

目前，已提出的组密钥安全协议可被分为3种基本类型[1]:(1)集中式组密钥管理.此方式存在一个中心机构,它为组内成员产生和分配组密钥, 当组内成员发生变化时更新组密钥，但是要在 Ad hoc网络中找到这样一个高可信度中心机构的难度较大.(2)分散式组密钥管理.在这种方式中, 一个大的群组被划分成若干个子组,每个子组存在一个子组协调员负责子组的密钥分发, 该方式仍然存在子组中心节点的问题, 而 Ad hoc节点对消息的中继传输使子组协调员有很大的通信负担.(3)分布式组密钥管理.由于Ad hoc网络中各节点的通信身份完全平等且组员关系经常发生变化, 所以其群组密钥管理方案适宜采用这种方式.该方式的特点是无中心机构、成员节点地位平等、分配给各节点的计算量和通信量开销量相同、组密钥由组成员协同运算产生, 但在网络规模较大的时候, 该方式一样存在远距离节点之间的中继通信量增大的问题.

针对Ad hoc网络的特点, 国内外学者已做了大量的研究工作,提出了许多安全高效的组密钥管理方案.2000年,Steiner等[2]提出了一个动态组密钥分发协议CLIQUES， 该协议支持节点加入、离开及网络分离等动态变化状态.Kim等[3]在GDHv.2协议[4]的基础上提出了基于树的组密钥分发协议TGDH 协议,其安全性和复杂性比原有协议有所提高.2004年,Kim等[5]又提出了基于二叉树的组密钥协商协议，适用于动态无组织网络.接着Kim[6]又提出了STR协议，该协议在结构上做出了较大的调整，不同于前者必须尽量保证结构的饱和性，结构变化更加灵活.2007年,Liao等[7]将TGDH和STR有机地结合在一起， 综合两种结构的特点提出了TFAN结构.以上结构都是基于公钥密码学、使用Diffie-Hellman密钥协商方式来实现动态的组密钥管理的,但这类算法性能不够理想, 特别是不具备认证功能, 存在一定安全隐患.后来，文献[8-10]提出了基于簇的组密钥管理方案,这些方案适用于大规模网络中的密钥管理，是针对Ad hoc网络中的分层结构提出的，具有一定的网络扩展性.

在已有的较为典型的组密钥管理方案中，密钥协商过程需要大量的计算开销存储资源或通信带宽，效率比较低,所以根据Ad hoc网络的特点，提出了一个安全有效的组密钥管理方案，提出的方案以增强安全性和减少计算量和通信量为目标. 该方案在系统初始化完成以后，组密钥的分发与重构完全由网络中节点的相互合作来完成，并且采用基于身份的密码体制来实现组密钥分发与重构过程中消息的安全传送.

1 相关基本知识

1.1 基于身份的密码体制

在1984年，Shamir[11]提出了基于身份的密码体制思想，以简化证书的管理.近年来，双向性映射和双向性Diffie-Hellman问题[12]的提出，使得基于身份的密码体制获得了长足的发展，人们提出了一系列基于身份的加密、签名及密钥交换协议.

基于身份的密码机制是建立在双向性e:G1×G1→G2映射上的(G1是q阶的加法群，G2是q阶的乘法群，q为一大素数),其安全性的基础是BDH假设，即给定P,aP,bP和cP(P是G1的一个生成元，a,b,c是有限域Fq中的随机数)，在多项式时间内确定e(P,P)abc是不可能的.系统的核心是一个密钥生成中心KGC，负责系统初始化时生成系统参数并根据节点的身份为其生成私钥.系统的建立过程为KGC随机选择一个私钥s∈Fq，计算PKGC=sP并公布(P，PKGC).计算出身份为ID节点的公/私钥对(QID，SID),QID=H(ID) (H:{0,1}*→G1),SID=sQID.

1.2 分布式主密钥生成

从上节的介绍可知，基于身份密码体制的认证私钥由式S=sH(ID)生成.显然,为了生成S，需要系统的主密钥s.为了解决Ad hoc网络无集中式KGC和拓扑结构易变化的问题，根据Shamir的(t,n)门限密钥方案，将s分解成n个分量(s1,s2,…,sn)，由n个节点分别保存.需要恢复s时，可由任意t个节点保存的s分量重构，而少于t个则无法恢复.基于拉格朗日插值公式产生s分量和重构s的过程如下.

设q为素数，Fq为有限域，随机选取s和t-1个系数a1,a2,…,at-1,在Fq上构建t-1次多项式f(x)=s+a1x+a2x2+…+at-1xt-1.计算第i个节点上保存s分量si,si=f(IDi),i=1,2,…,n.根据Lagrangue插值公式，任选t个si就可以重构t-1次多项式：

(1)

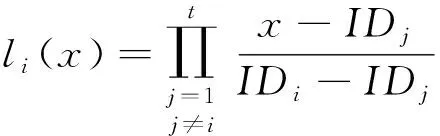
(2)

2 组密钥管理方案

2.1 系统的初始化

系统的初始化工作由一个临时管理中心来完成,临时管理中心可以由一个资源比较充分的节点来担当，当初始化工作完成以后，此节点临时管理中心的作用就消失.

假设系统由n个节点组成，每个节点Ni拥有唯一全局标识符IDi，i=1,2,…,n.

(1)临时管理中心首先生成系统参数q，G1，G2，e：G1×G1→G2和4个哈希函数H1:{0,1}*→G1,H2:G2→Fq，H3:G2→{0,1}1(1为会话密钥的长度),H4：{0,1}*×G1→Fq.然后,随机选取s∈Fq作为系统的私钥,并计算出系统公钥Ppub=sP.最后，向系统中所有的节点公开系统参数(P,Ppub,H1,H2,H3,H4).

(2)按1.2节算法为系统中节点Ni生成系统私钥分量si，并通过安全通道传送到节点Ni上；

(3)计算节点Ni的私钥Si=sH1(IDi)，并通过安全通道传送到节点Ni上.

2.2 组密钥生成协议

当系统初始化完成以后，系统中所有的节点按下列步骤共同产生组通信密钥.

(1)节点Ni随机首先选取ri∈Fq为该节点的私有参数，然后计算Qi=H1(IDi)，Ti=riP,Pi=H2(e(Qi,Ti))Si.计算完成后，把发送给节点Ni-1和Ni+1(这里当i=1时,i-1=n;当i=n时，i+1=1).

(2)当节点Ni收到节点Ni-1和Ni+1发来的消息 (j=i-1,j+1)后，首先验证等式e(Qi,Pj)=e(Si,H2(e(Qj,Tj)Qj))是否成立.如果都成立，计算

Di=e(Ti+1-Ti-1，ppub)ri,

(3)

Vi=H2(Di)Si.

(4)

这里,当i=1时,i-1=n;当i=n时,i+1=1.

计算完成后，节点Ni把广播出去.

(3)节点Ni收到节点Nj发来广播消息(j=1,2,…,n,j≠i)后，首先验证等式e(Qi,Vj)=e(Si,H2(Dj)Qj)是否成立.如果等式成立，用下式计算系统的组通信密钥：

(5)

2.3 新节点加入协议

当有新节点加入时，系统首先需要更新组通信密钥.另外，还要为新加入的节点安全地生成系统主密钥分量.假设新加入的节点为Nn+1,标识符为IDn+1.

(1)节点n+1首先随机选取rn+1∈Fq为自己的私有参数，并计算Qn+1=H1(IDn+1),Tn+1=rn+1P.然后,在系统中随机选取t个节点Ni，计算Wi=e(rn+1Ppub,Qi).

计算完成后，节点n+1把发送给节点Ni

(2)当节点Ni收到节点Nn+1发来的消息后,首先验证等式Wi=e(Tn+1,Si)是否成立，如果等式成立并且允许节点Nn+1加入系统，节点Ni就进行下列计算:

① 节点Nn+1的私钥分量

(6)

② 节点Nn+1上需保存的系统密钥分量的子分量

(7)

③kh=H3(e(Ppub,H1(Kcur))) ,这里的Kcur是当前的组通信密钥.

ki=H3(e(Qn+1+Qi，Tn+1)ri),

(8)

Ci=Eki(Sn+1，i‖sn+1，i‖kh),

(9)

其中,Eki(.)表示用ki对消息进行加密运算，‖表示连接符号.

④Ri=H4(Ci,H1(ki)).

当所有的计算完成后，节点Ni把发送给节点Nn+1.

(3)当节点Nn+1收到节点Ni发来的消息 后计算

ki=H3(e(Qn+1+Qi，Ti)rn+1).

(10)

求出ki后,验证等式Ri=H4(Ci,H1(ki))是否成立.如果验证成功,就用ki解密收到的密文Ci，得到Sn+1,i,sn+1,i,kh.如果某些节点发来的消息没有通过验证，就再选一些节点，发出加入请求，直到节点Nn+1收到t个节点发来的正确信息.

如果节点Nn+1成功地收到t个节点发来的信息，就开始计算：

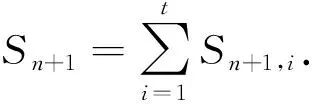
③ 新组通信密钥Knew=kh⊕kc,其中，kc=H2(e(Qn+1,rn+1P)).

④M=Ekh(kc),U=rn+1Qn+1,V=(rn+1+H4(M,Qn+1))Sn+1.

当计算完成后,节点Nn+1把广播给系统中所有的节点.

(4)当节点Nj(j=1,2,…,n)收到新加入节点Nn+1发送来的消息后，首先验证等式e(P,V)=e(Ppub,U+H4(M,Qn+1)Qn+1)是否成立.

如果等式成立，计算kh=H3(e(Ppub,H1(Kcur))),然后用kh从收到的密文M中解密出kc,最后用解出的kc计算新的组通信密钥Knew=kh⊕kc.

2.4 成员离开/组密钥的更新协议

当有节点离开系统或由于长时间使用后需要更新组密钥,这时由系统中任一节点(假设是节点Ni)发起，进行以下计算:

(1)节点Ni首先选取一随机数ri∈Fq为自己的新私有参数,然后计算kh=H3(e(Ppub,H1(Kcur))) .这里，Kcur是当前的组通信密钥.

kc=H3(e(riP,Qi)),M=Ekh(kc),U=riQi,V=(ri+H4(M,Qi))Si,计算完成后，节点Ni把向系统中其他节点广播.

(2)当节点Nj(j=1,2,...,n,j≠i)收到节点Ni广播的信息后，首先验证等式e(P,V)=e(Ppub,U+H4(M,Qi)Qi)是否成立，如果等式成立,计算kh=H3(e(Ppub,H1(Kcur))).

然后,用kh从收到的密文M中解出kc,最后用kh和kc计算出新的组通信密钥Knew=kh⊕kc.

3 协议分析

3.1 协议安全性分析

就基于身份的密码体制而言，密钥管理协议的安全性主要是系统主密钥的安全性，因为由主密钥可以计算出任意用户的私有密钥.本方案中,系统的主密钥是在系统组建初期由系统中所有的节点共同生成的，不需要用户间存在安全通道和可信第三方，所以避免了可信中心受到攻击而引起系统主密钥泄露的问题.而且,本研究还使用文献[4]和文献[12]中加解密算法保护节点间私钥分量的传输，从而保证只有合法节点可以产生认证私钥.虽然各节点生成的私钥分量是以明文形式传输的,但每个节点的私钥分量除了其他所有节点贡献的私钥子分量外，还包括节点本身提供的私钥子分量，而这部分只有节点本身知道.另外,节点私钥分量以及主公钥分量在节点间传输时，都会对消息进行基于身份的签名，从而保证了消息的完整性.为了保证系统主密钥的安全性，该方案采用(t,n)门限共享方案为每个组节点生成部分共享密钥.当系统初始化完成以后，任何不超过t个的节点都无法重构节点的私有密钥.

该方案还提供了以下的安全保证：(1)隐式密钥认证.除了系统的合法参与者，其他任何用户都不能计算出协商出来的组通信密钥.因为虽然非法用户可以得到所有合法节点发送给某个节点的所有Di，但在计算组密钥时还需要该节点的私有参数ri，而每个节点的私有参数只有自己知道.(2)会话密钥的独立性.某次会话密钥的泄露不会影响到其他次协商的会话密钥的保密性.在协议中，每次组密钥的生成都包含有新的随机信息.(3)前向安全性与后向安全性.因为在协议中，无论是有新节点加入或是有节点退出，系统都会更新组通信密钥的，而每次会话密钥的生成都包含有新的随机信息，所以离开的用户无法计算出以后的组密钥，新加入的用户同样也无法推算出前面的组密钥.

3.2 协议效率分析

通信开销和计算开销是衡量组密钥管理方案性能优劣的一个重要标准.该方案的通信开销对于初始组密钥协商协议需要n次广播通信和n次点到点的通信，节点加入时需要2t次单点通信和1次广播通信，而节点离开时只需要1次广播通信数.本方案中所使用的加密算法都是对称加密算法，而且加入协议和离开协议所需的计算量的复杂度也都是常数.

下面通过与CLIQUES协议、TGDH协议和STR协议在通信开销和计算开销方面的比较，来分析验证本方案的性能.4种族密钥管理方案的通信量和计算量的比较如表1所示.协议的总轮数是固定的,这就意味着协议的通信规模与组成员的数目无关,而 CLIQUES和TGDH的通信规模与组成员数目成正比，STR协议的总轮数比本协议多一次.在运算量方面，本协议运算的复杂度是常数，这样本协议适合应用在大的Ad hoc网络中.

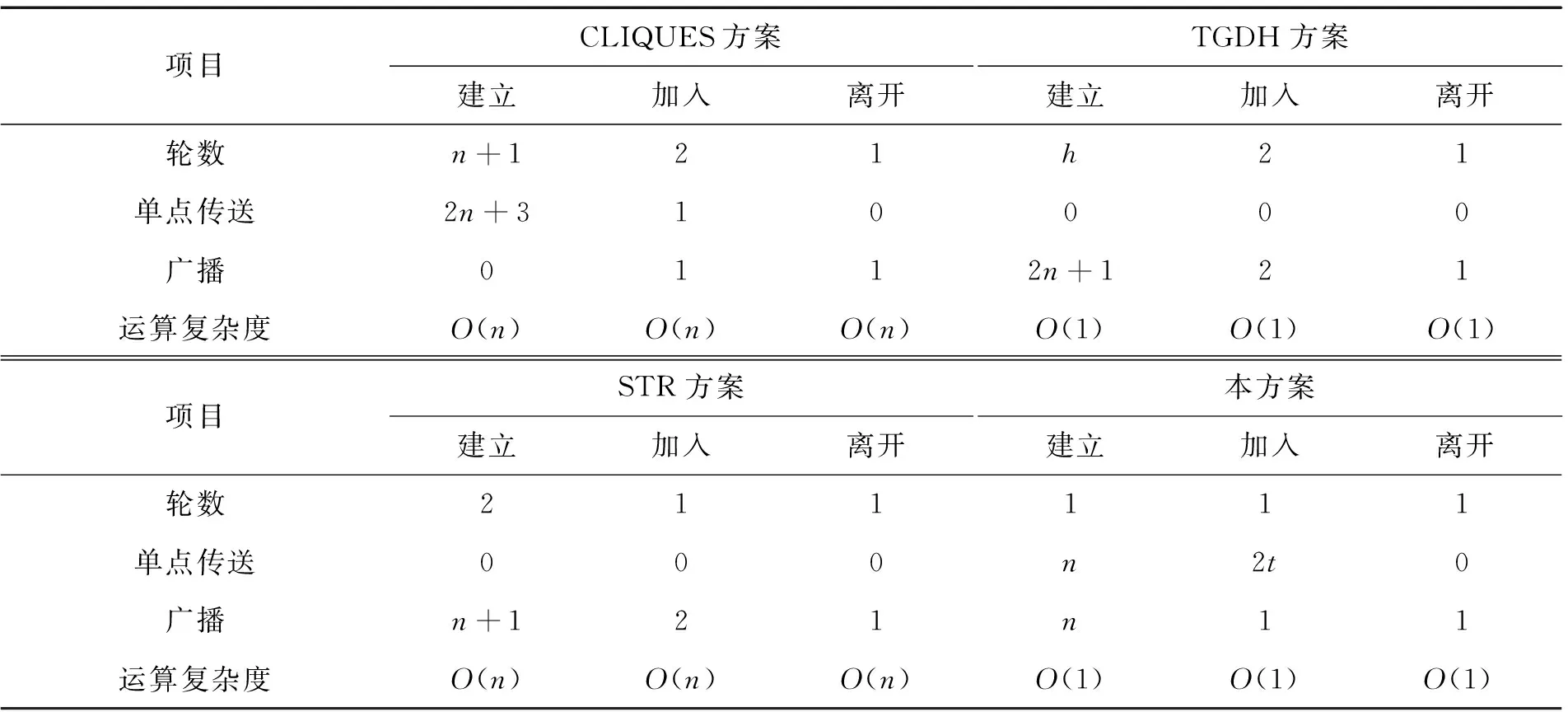
表1 本方案与其他组密钥管理方案性能的比较Tab.1 Performance comparison

4 结束语

Ad hoc网络的分布式组网方式、动态的网络拓扑和有限的带宽资源，使得传统的基于信任中心的组密钥管理方案不适合Ad hoc网络.首先分析了基于身份的密码体制，讨论了如何使用Lagrange插值公式生成基于身份密码体制的系统主密钥，然后给出了组密钥的生成方法和节点加入/离开时系统组密钥的更新方法.该方法具有分布式实现和安全高效的特点，在网络中部分节点失效的情况下仍能有效地更新组通信密钥，能够满足Ad hoc网络在恶劣的网络攻击环境中安全工作的要求.

参考文献：

[1] 熊万安,许春香.一种新的基于ECC的Ad hoc组密钥协商协议[J].重庆邮电大学学报：自然科学版,2011,3(1):101-106.

[2] Steiner M，Tsudik G，Waidner M.Key agreement in dynamic peer groups[J].IEEE Transactions on Parallel and Distributed Systems，2000，11(8)：56-61.

[3] Kim Y,Perrig A T，Sudik G.Simple and fault-tolerant key agreement for dynamic collaborative groups[C]∥Proceedings of the 7th ACM Conference on Computer andCommunication Security.New York:ACM,2000:235-244.

[4] Steiner M,Tsudik G,Waidner M. Diffie-Hellman key distribution extended to group communication [C]∥Proceedings of the 3rd ACM Conference on Computer and Communications Security.New York:ACM,1996:31-37.

[5] Kim Y，Perrig A，Tsudik G.Tree-based group key agreement[J].ACM Transactions on Information and System Security，2004(71)：60-96.

[6] Kim Y,Perrig A，Tsudik G. Group key agreement efficient in communication [J].IEEE Transactions on Computers，2004，53 (7)：70-73.

[7] Liao L，Manulis M.Tree-based group key agreement framework for mobile ad-hoc networks[J].Future Generation Computer Systems，2007(23)：787-803.

[8] Shi H,He M,Qin Z. Authenticated and communication efficient group key agreement for clustered Ad hoc networks[J].Lecture notes in computer science,2006，43(1):73-89.

[9] Hietalahti M.A clustering-based group key agreement protocol for ad-hoc networks[J].Electronic Notes in Theoretical Computer Science,2008(192):43-53.

[10] Elisavet K.Efficient cluster-based group key agreement protocols for wireless Ad hoc networks[J].Journal of Network and Computer Application,2011(34).384-393.

[11] Shamir A.Identity-based cryptosystems and signature schemes [C]∥Proceedings of Crypto′ 4,Lecture Notes in Computer Science.New York 1984:47-53.

[12] Bong D，Franklin M.Identity-based encryption from weil pairing [C]∥Proceedings of Crypto′ 1,Lecture Notes in Computer Science.New York，2001:213-229.