网格下基于模糊逻辑的信任修正模型
2013-11-20于海鹏李运娣
于海鹏,李运娣
(河南工程学院 计算机科学与工程系,河南 郑州 451191)
近年来,随着分布式系统的广泛应用,其安全问题也越来越引起人们的重视,很多学者针对开放分布系统的动态性、匿名性等特点进行了相应的研究,以期克服传统安全机制的缺陷,建立新的更加灵活的安全管理机制[1- 2].开放模式的网格系统同样面临着系统的安全问题,建立好的信任管理机制是实现网格安全的重要前提,也是网格系统能够得以大规模发展的关键.网格信任主要分为两类:身份信任和行为信任[3].身份信任主要是基于静态的认证和访问控制等机制来实现的,这已不能满足网格发展的需求.行为信任也叫主观信任,它以现实世界中人与人之间的信任关系为依托,借助数学模型来对网络中的信任关系进行建模[4- 5].这些模型考虑了信任的主观性,提出了不同的形式化推理方法,但这些信任机制都没有考虑到信任本身所具有的模糊性和不确定性.参照现实世界中人们之间的信任关系,模糊逻辑更确切地描述了网络中的这种主观信任关系.文献[6]运用资源站点的交易成功率和自身的入侵防御能力进行模糊推理,来增强网格系统的安全性能,但没有对信任的传递过程进行推理.文献[7]根据资源站点自身的信任值进行模糊推理得到推荐信任值,但它们都没有考虑节点历史推荐信息对信任的影响.本研究以模糊理论为基础,考虑推荐信息的真实性对网格安全性能的影响,给出了一个开放网格环境下强健的信任修正评估模型,该模型不但能够有效地对节点起到激励作用,并且能防止网络中的恶意推荐与攻击.
1 信任向量的建立及信任推理
模糊性是指客观事物在性态及类属方面的不明确性,是客观世界中某些事物本身所具有的一种特性,它所反映的事物本身是模糊不清的.信任具有主观性,它是一种主观判断,在很大程度上依赖于观察者.同时,由于对对方的不了解或不完全了解,信任又表现出不确定性.信任的主观性和不确定性使信任本身及其相关特征都表现出模糊不明的特点,所以在对信任进行度量时需要充分考虑其模糊性特点.模糊逻辑是为了解决现实世界中普遍存在的一些不确定性(模糊性)问题而提出的,模糊逻辑能够为主观信任的研究提供一种有效的度量方法.
定义1 设U为论域空间,u为U中的元素,对任意的uU存在如下映射:U→[0,1],u→μA(u)[0,1],则称由μA(u)所构成的集合A为U上的一个模糊集,μA(u)为u对A的隶属函数.对某个具体的u而言,称μA(u)为u对A的隶属度.
在开放网格环境中,论域U为主体集,主体间的信任等级表述为U上的多个模糊子集.用离散的标度来描述主体信任的高低,设UL={L1,L2,…,Lm}为信任论域,信任等级分为m级,其中Lj(j[1,m])为第j级信任,则主体的信任度隶属函数在各信任等级处的隶属度所构成的向量为信任度向量,用L={l1,l2,…,lm}表示.
对实际的信任度向量的度量一般有两种途径,一是直接信任,通过主体与主体间直接的交互经验采用模糊综合评价的方法进行计算;二是推荐信任,通过对已有的信任度向量进行形式化分析和推理,得出新的信任度向量.
1.1 直接信任的综合评判
在网格资源访问过程中,往往需要对资源进行多方面的考虑,如资源的稳定性、可靠性、易用性等,这些构成了对网格资源信任评价的因素集,即资源属性集合,用S={S1,S2,…,Sn}表示,其中Si表示请求节点对资源提供节点信任评判的第i方面因素.从属性到评价的模糊关系为V=S×L=(vij)n×m,其中vij表示对Si作出Lj评价的可能性.对于不同的资源访问,请求节点对资源的各个属性关心的侧重点不同,故对资源各属性依据请求节点的关心度给定一个相应的权重值,用λ=(λ1,λ2,…,λn)表示,其中λ1+λ2+…+λn=1.设Tab(t)表示在网格资源交互过程中,请求节点xa对资源提供节点xb在时间t就某次特定交互的信任评价向量,则:
Tab(t)=λ·R.
(1)
信任具有时效性,它是一个随时间变化而进化的关系,随着时间的持续,历史信任度也将不断地衰减.假定节点xa和xb在t时刻进行交互,在此前节点对节点的信任评价为DTab(t-1),则交互后信任向量更新为
DTab(t)=αDTab(t-1)+(1-α)Tab(t),
(2)
其中,α∈[0,1]是衰减控制因子,主要反映历史信任的衰减度,交互间隔的时间越长,历史信任就越不可靠,α的取值就越小.
1.2 间接信任的形式化推理
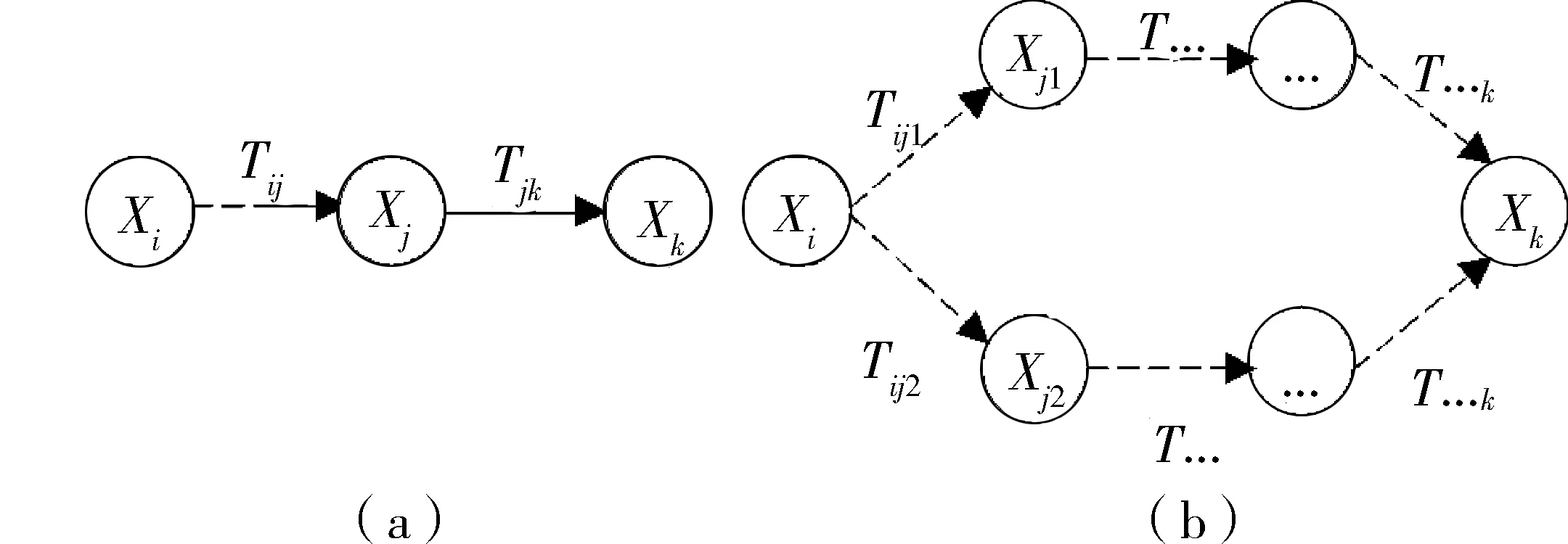
图1 信任的传递与合成Fig.1 Transfer and synthesis of trust
当一个节点要在网格系统中查找某个资源时,对于查找到的能够提供该资源的服务节点,有的可能是以前有过交易的节点,有的可能是陌生节点.对于陌生节点,需要根据其他节点的信任推荐来决定是否进行交互,这就需要处理由于信任推荐导致的信任传递和多重信任关系的合成问题.根据文献[8]可知,信任的传递不会增加信任值,同时多重信任关系的合成不会减少信任值,依据此原则对网格系统中的间接信任进行形式化推理,如图1所示.
为了便于计算,在网格系统的每个节点中保存了一个与该节点有过直接交互的节点信任评价表TBL1,TBL1中保存了资源提供节点的相关信息和资源请求节点根据公式(1)与(2)计算出的对资源提供节点的直接信任度评价,同时也保存了一个对该节点提供过推荐信息的节点的推荐评价表TBL2.TBL2中保存了推荐节点的相关信息和资源请求节点根据公式(10)计算出的对推荐节点的推荐信任度评价,根据本地节点保存的直接信任度与推荐信任度来达到对目标节点的可信度的评价.考虑到现实生活中,人们总是容易对可信度高的人所述事情给予一个高的认可度,对可信度低的人所述事情的认可也较低,所以对推荐主体所推荐的另一主体的信任度向量,即判断主体的认可程度与推荐主体自身的信任度向量有很大关系.但是,在网络中也存在这样的情况,一个资源提供节点总是能提供质量较高的资源给资源请求节点,但作为资源推荐节点,该节点可能不负责任地进行随意推荐或者和其他节点串通起来进行恶意推荐,这也会导致网络中的交易失败率增高.因此,有必要对节点的推荐信息进行评价,这也是影响推荐主体的推荐认可度的一个因素.对图1(a)所示的关系,节点xi需要通过与节点xj的直接信任度向量和推荐信任度向量,来综合判断对xj推荐的主体xk的信任度的接受程度,即Tik=η·Tjk.其中,η是判断主体对推荐主体的推荐接受系数,η的值跟请求节点与推荐节点的直接信任度向量与推荐信任度向量有关,η[0,1].
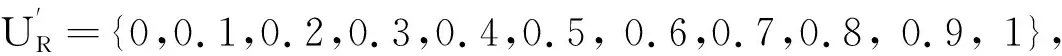
Rule 1: IFLis “不信任” andGis “不信任” thenRis “不接受”
Rule 2: IFLis “不信任” andGis “有点信任” thenRis “不接受”
Rule 3: IFLis “不信任” andGis “一般信任” thenRis “不接受”
Rule 4: IFLis “不信任” andGis “很信任” thenRis “不接受”
Rule 5: IFLis “不信任” andGis “完全信任” thenRis “不接受”
…… ……
Rule 21: IFLis “完全信任” andGis “不信任” thenRis “不接受”
Rule 22: IFLis “完全信任” andGis “有点信任” thenRis “部分接受”
Rule 23: IFLis “完全信任” andGis “一般信任” thenRis “基本接受”
Rule 24: IFLis “完全信任” andGis “很信任” thenRis “总体接受”
Rule 25: IFLis “完全信任” andGis “完全信任” thenRis “完全接受”
以上规则中,L表示请求节点与推荐节点的直接信任度向量,G表示推荐节点的推荐信任度向量,R表示与L和G对应的接受程度向量.对于以上规则,首先选择L和G中信任度较低的向量记为A,则A为根据请求节点与推荐节点的直接信任度向量和推荐信任度向量得到的新的信任度向量.判断主体对推荐信任的接受程度与信任度向量A的可信度有关,所以根据信任度向量可以直接得到对应的接受程度向量.令τ(k)=Lk×Rk,则
μτ(k)(x,y)=μLk(x)∧μRk(y),
(3)
其中,1≤k≤5,xUL,y表示由UL到的第k条模糊关系,μLk表示语言值向量Lk在x处的取值,μRk表示向量Rk在y处的取值,所以
(4)
根据请求主体xi与推荐主体xj之间的直接信任度向量与推荐信任度向量,得到新的信任度向量Aij,运用模糊推理可计算出xi对xj的推荐的接受程度向量r′:
r′=Aij·τ.
(5)
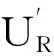
(6)
其中,ρi在ρi处取大于或等于可以被采纳的阀值(例如设为0.5),k为隶属度大于阀值的总数.把上面的一个主体推荐的情况进行推广,可得到主体xi经推荐链上多个主体的推荐求取主体xn的信任度向量的计算问题:
Tin=η1·η2·…·ηn-1·Tjn-1k,
(7)
对多重信任关系的合成如图1(b)所示,xi从两条不同的路径得到了关于目标节点xk的信任度向量,信任的合并就是要根据已有的信任度向量得到xi对xk的新的信任度向量Tik.假定T1和T2是xi从两条路径上得到的关于目标主体xk的推荐信任度向量,η1和η2为计算得到的对T1和T2的接受系数,则xi对xk的新的信任度向量Tik为:
(8)
以上的计算进行推广,把主体xi经过多条路径得到xk的多个推荐信任度向量进行合成计算,可得到新的Tik的计算问题:
(9)
其中,η=η1+η2+…+ηn.
2 推荐信任度的初始化与修正
2.1 推荐信任度的初始化
对节点的推荐信息表TBL2,在每次推荐结束后,更新请求节点对推荐节点的推荐信任度向量RT.推荐主体的推荐的信任度隶属函数,在UL各信任等级处的隶属度所构成的向量设为G={g1,g2,…,gm}.对于具体的推荐过程,设RTab(t)为xa对xb在时间t就某次特定推荐的信任评价向量,则推荐后xa根据RTab(t)对xb的推荐信任度进行更新.如果此次推荐是xb第一次向xa进行资源推荐,则首先依据两节点间是否有过交互再对RTab进行初始化,如果两节点有直接交互则取xa对xb的直接信任度评价DTab作为xa对xb的初始推荐的信任度评价向量,否则直接初始化为{0,0,…,0,1},然后把RTab放入节点xa的TBL2表中.此次推荐后的信任度更新为
RTab(t)=αRTab(t-1)+(1-α)RTab(t),
(10)
其中,α∈(0,1),为时间衰减因子,其取值的大小依据对历史评价信息的依赖程度.
2.2 推荐信任度的修正计算
对两个向量A={a1,a2,…,an}和B={b1,b2,…,bn},定义它们的相近函数为
(11)
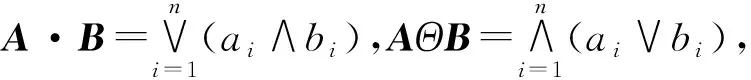
(12)
假定节点xi根据xj的推荐与节点xk进行了交互,交互后节点xi对此次交互的直接信任度评价为Tik,xj对节点xk的直接信任度为Tjk,根据公式(11)计算Tik与Tjk的相似度φ=δ(Tik,Tjk).如果φ比较合理,则依据φ给出此次推荐中xi对xj的推荐信任度评价向量RTij(t);如果φ值太小(这里假定为 0.2),则需要对此次推荐进行进一步的考察,以决定是否对φ进行修正,然后再根据修正后的φ重新给出对xj的推荐信任度评价向量RTij(t),过程如下:
(1)根据Tik与Tjk计算φ,如果φ值过小则进入下一步进行修正,否则转(5) ;
(2)查找节点xi中关于节点xj的直接信任度向量DTij(t)和推荐信任度向量RTij(t-1),如果这两个值中有一个信任度评价值较低,则转(5);
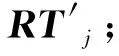
(4)令σ=1-δ(RTij(t),RT′),则对δ(Tik,Tjk)的修正为φ=δ(Tik,Tjk)=β·δ(Tik,Tjk)+(1-β)·σ,其中β∈(0,1)为修正系数.
(5)根据修正过的φ值重新给出xi对xj的推荐信任度评价向量RTij(t).
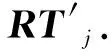
3 系统性能分析与模拟实验
在网格系统中通过增加对推荐信任的控制策略,能更好地实现对客户的访问控制,避免网络中的欺诈行为,提高系统的强健性.假定在网格的信任传递中,请求节点表中保存的推荐节点的直接信任度向量为dt={0,0,0.3,0.6,0.8},推荐信任度向量为rt={0.9,0.5,0.2,0,0}.
令R1={1,1,0.8,0.5,0,0,0,0,0,0,0},R2={0,0.5,1,1,1,0.5,0,0,0,0,0},R3={0,0,0,0.5,1,1,1,0.5,0,0,0},R4={0,0,0,0,0,0.5,1,1,1,0.5,0},V5={0,0,0,0,0,0,0,0.5,0.8,1,1},则由公式(4)和(5)得

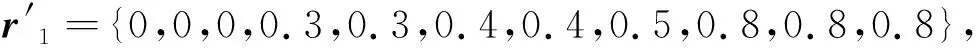
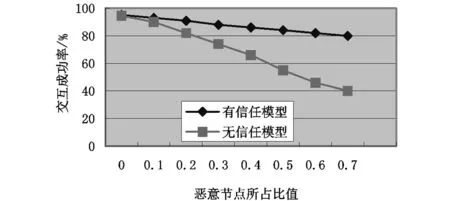
图2 交互成功率对比图Fig.2 The interactive success rate comparison chart
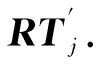
为了证实分析结果,对基于本研究的网格信任模型进行了仿真实验.并在各类参数相同的情况下,对有无本模型的两种情况进行了对比实验.实验中构造多个资源,各个资源文件在网络中的节点上随机分配,同时构造多个任务,每个节点执行一个或多个请求任务,然后比较在恶意节点比例不同的情况下任务的完成情况,实验结果如图2所示.
从图2可以看出,在系统中运用此模型能有效地防止节点的恶意行为,提高交互的成功率.
4 结束语
针对开放网格环境存在的安全问题,本研究提出了一种有效的信任管理模型.该模型充分考虑了信任的主观性与模糊性以及信任关系的复杂性和时效性,以模糊逻辑为基础,对直接信任度很好地进行了综合评价.同时,结合模糊集合论的优势,重点对信任的传递过程进行了推理,对多重信任关系的合成进行了计算.由于在信任的传递过程中考虑了推荐信任的影响,该模型在面对网络中的恶意推荐与攻击时有较好的防御性.
参考文献:
[1] Blaze M,Kannan S,Lee I,et al.Dynamic trust management[J].Computer,2009,42(2):44-52.
[2] Yu B,Singh M P,Sycara K.Developing trust in large-scale peer-to-peer systems[C]∥2004 IEEE 1st Symposium on Multi-Agent Security and Survivability.New York:Institute of electrical and Electronics Engineers Inc,2004.
[3] Azzedin F,Maheswaran M.Evolving and managing trust in grid computing systems[C]∥Proceedings of IEEE Canadian Conference on Electrical&Computer Engineering.Winnipeg:IEEE Press,2002.
[4] Wang Y,Vassileva J.Bayesian network-based trust model in peer-to-peer networks[C]∥Moro G.Proceedings.of the 2nd Int’1 Workshop on Agents and P2P Computing.Berlin:Springer-Verlag,2004.
[5] Jameel H,Hung L X,Kalim U, et al.A trust model for ubiquitous systems based on vectors of trust values[C]∥Proceedings.of the 7th IEEE Int’1 Symp.Washington:IEEE Computer Society Press,2005.
[6] Song S H,Wang K.Fuzzy trust integration for security enforcement in grid computing[C]∥The Int’1 Symp.on Network and Parallel Computing.Berlin:Springer-Verlag,2005.
[7] 唐文, 胡建斌, 陈钟. 基于模糊逻辑的主观信任管理模型研究[J].计算机研究与发展,2005,42(10):1654-1659.
[8] Sun Y, Yu W, Han Z. Information theoretic framework of trust modeling and evaluation for Ad hoc networks[J].IEEE Journal on Selected Areas in Communications,2006, 249(2):674-679.
